全站仪导线测量若干问题的探讨
2010-10-25郭宗河郑进凤贺可强
郭宗河, 郑进凤, 贺可强
(青岛理工大学 土木工程学院,山东 青岛 266033)
全站仪的出现,给测量工作带来了越来越多的方便。与传统光学测量仪器相比,全站仪最大的特点就是便捷、高效:既能自动测量斜距、竖直角、水平角,又能自动记录、计算并显示出平距、高差、坐标差等相关数据;在此基础上,通过内置的程序功能还可以完成一些更加复杂的测量工作,比如“对边测量”、“悬高测量”、“三维坐标测量”、“导线测量”等。下面,就全站仪导线测量的若干问题做些探讨。
1 基本概念、原理与方法
所谓“全站仪导线测量”,一般是指利用全站仪通过内置的程序功能进行“导线型”坐标测量,即全站仪“三维坐标测量”的连续进行,如图1所示。
图1中,A、B为2个已知点,1、2……为欲测定的目标点,首先将全站仪安置在已知点B,输入B点的坐标(¯xB、¯yB)和高程¯HB、仪器高i、目标高v(不需要测定高程时,可只输入坐标),并瞄准另一已知点A进行定向;然后照准目标点1上的反射棱镜进行测量,仪器即可按(1)~(4)式自动计算并显示出测站点B至目标点1的水平距离D、目标点1的坐标(x1、y1)和高程 H1(此即为“全站仪三维坐标测量”)。
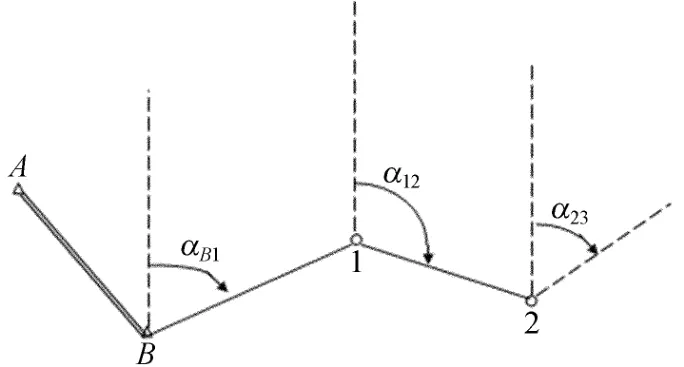
图1 全站仪导线测量示意图
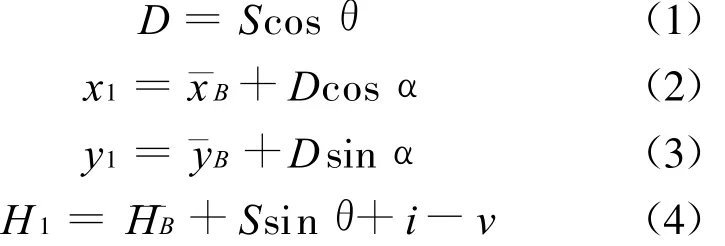
其中,S为全站仪至反射棱镜的斜距;θ为全站仪至反射棱镜的竖直角;α为测站点B至目标点1的方位角(可见,全站仪三维坐标测量的实质是利用极坐标法测定目标点的平面坐标,用三角高程法测定目标点的高程)。
然后,将目标点1作为新测站,原测站点B作为后视点,全站仪迁至测站点1,同法继续向前测定新目标点2的三维坐标,以此类推。
可见,全站仪导线测量的形式实际上为三维支导线,且角度的观测为半测回,高差的测定为单向观测。另外,为了免去除了第一次以外的各次测量中的测站点和后视点的坐标输入,全站仪还设有自动“置换测站坐标”功能——把原测站点的坐标置换为后视点坐标,原目标点的坐标置换为测站点坐标。
2 平差计算
由上面的介绍可知,全站仪导线测量可实现快速测量,并实时地自动计算、显示和储存各点的三维坐标;但由于其形式实际上为三维支导线,且角度的观测皆为半测回而缺乏检核。因此在实际工作中,全站仪导线测量一次发展支点不宜过多、路线不能过长;否则,应从一已知点出发测至另一已知点以资校核,如图2所示。此时,则存在成果检核和平差计算问题。

图2 全站仪附合导线测量示意图
2.1 坐标闭合差的计算与调整
如图2所示,从一已知点B和已知边BA出发,利用全站仪导线测量模式,依次测定出目标点1、2……的坐标(),直至另一已知点 C。由于存在测角、测距误差,最后测得的C点坐标()将不等于 C 点的已知坐标(),从而产生坐标闭合差,即

由此,可算得导线全长闭合差f和相对闭合差k,即

其中,∑D为导线各边长的总合,即导线全长。
若算得的导线全长相对闭合差k小于容许相对闭合差k容,则认为外业施测成果合格,并可转入内业平差计算。
关于上述全站仪导线测量的内业平差计算,普遍认为:由于全站仪导线测量可直接自动地计算、显示和储存各点的坐标观测值,同时也为了内业计算的简单、方便、快捷,直接按坐标观测值进行近似平差计算最为适宜,且已达成共识。但如何直接按坐标观测值进行近似平差计算,特别是如何计算坐标改正值却有不同的见解,概括起来可归纳为以下2种主要方法。
方法一:按与距离成正比平差法[1-4],各点的坐标改正值按(9)式、(10)式计算。
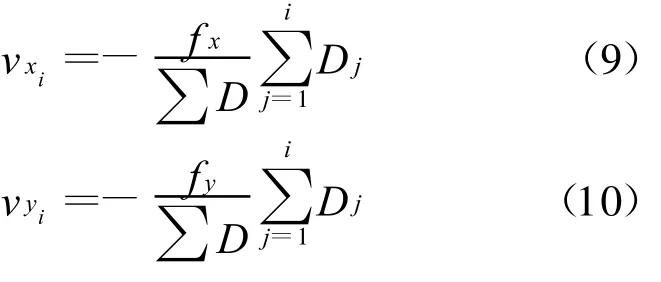
其中,Dj为各导线边的边长。
方法二:按与坐标增量成正比平差法[5,6],各点的坐标改正值按(11)式、(12)式计算。

利用(9)式、(10)式或(11)式、(12)式算得坐标改正值后,按(13)式、(14)式即可求得各点的坐标平差值,即

“方法一”在有关文献中采用的较多,但都未加推证。“方法二”在文献[5]中虽有推证,但是在假定“坐标增量为观测值,并取其绝对值的倒数为权”的前提下推导出的(11)式、(12)式,而为何“取坐标增量绝对值的倒数为权”未见任何解释(文献[6]中无推证)。为比笔者从误差分析的角度作以下探讨。
由(2)式可得:

对(15)式取全微分,有:

转换为中误差,则为:

在全站仪的设计中,关于测距和测角的精度一般遵循等影响的原则[7],即
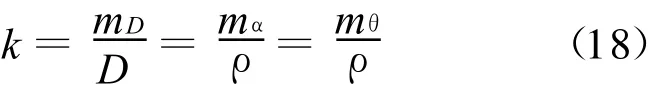
将(18)式代入(17)式,可得:

同法,可推得:

由(19)式和(20)式可知,坐标增量的误差并非与坐标增量的绝对值成正比,而是与导线边长成正比,因此“方法二”的前提条件不成立。同时,也证明了“方法一”的合理性。
2.2 高差闭合差的计算与调整
如图2所示,从一已知点B出发,利用全站仪导线测量模式,在依次测定出目标点1、2……坐标()的同时测定出其高程 Hi,直至另一已知点。由于存在测角、测距误差,最后测得的C点高程HC将不等于C点的已知高程¯HC,从而产生高差闭合差 fh,即

目前,关于全站仪导线测量高差闭合差的计算与调整,有关讨论较少,只在文献[1]中给出各点高程改正值和平差值的计算公式,即
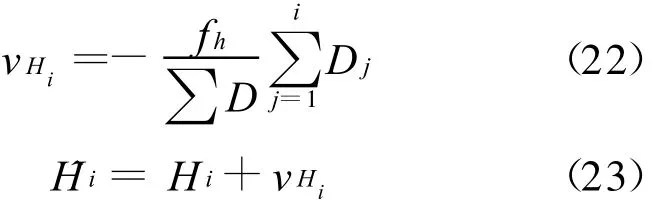
但同坐标平差一样,文献中并没有推证。下面,也从误差分析的角度作一探讨。
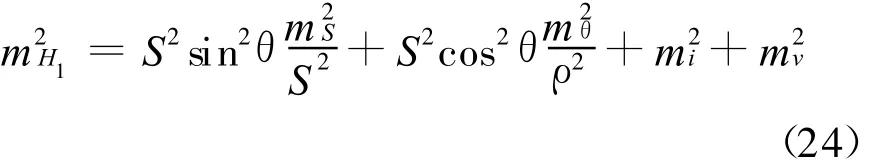
由(4)式,根据误差传播定律,可得1点的高程中误差,即考虑到仪器高、目标高的误差属于固定误差,并顾及(18)式,(24)式可写为:

由(25)式可知,全站仪导线测量高程的误差与导线边长近似成正比关系。因此,可以认为利用(22)式和(23)式对全站仪导线测量的高程进行近似平差还是比较合理的。
3 结束语
全站仪导线测量的实质为全站仪“三维坐标测量”的连续进行,其中许多的计算工作已由仪器内存的程序自动完成,可方便、快捷地显示出各待测点的三维坐标。然而,由于其形式为三维支导线,缺乏检核,因此在实际工作中,全站仪导线测量一次发展支点不宜过多、路线不能过长;否则,应从一已知点出发测至另一已知点以资校核。
若与已知点进行了附合,则可按(5)~(8)式和(21)式计算闭合差,进行成果检核;合格后,再分别按公式(9)、(10)、(13)、(14)和(22)、(23)进行近似平差,求得各待测点的最终坐标和高程。
最后,建议全站仪生产厂家不断完善其机内程序,从而给广大用户提供更多的便利。
[1] 聂 让.全站仪与高等级公路测量[M].北京:人民交通出版社,1997:188-193.
[2] 潘 威.公路工程实用施工放样技术[M].北京:人民交通出版社,2004:38-41.
[3] 耿丙颜,韩合轩,李传明.全站仪与三维坐标导线测量[J].河南交通科技,1999,19(3):20-22.
[4] 张平风.坐标导线测量及其近似平差计算[J].山西建筑,2006,32(16):339-340.
[5] 罗科勤.关于《电子速测仪坐标导线平差计算方法》的讨论[J].测绘通报,2001,(6):46-47.
[6] 邱健壮,赵燕,李宗才.全站仪观测导线测量平差方法的研究[J].山东农业大学学报(自然科学版),2003,34(1):96-99.
[7] 邹永廉.土木工程测量[M].北京:高等教育出版社,2004:127.
[8] 郭宗河,董宇阳,郑进凤.测量学实用教程[M].北京:中国电力出版社,2006:101-109.
