体外预应力加固混凝土双向板的力学性能分析

胡 成, 吴 元

(1.合肥工业大学土木与水利工程学院,安徽合肥 230009;2.东南大学土木工程学院,江苏南京 210096)

0 引 言

体外预应力加固技术自20世纪80年代以来开始用于我国公路桥梁的加固工程中,现已在国内外工业和民用建筑的加固实践中得到了相当广泛的应用[1-5]。相对混凝土梁而言,目前在体外预应力加固钢筋混凝土双向板方面的研究国内外都较缺乏,本文通过对张拉体外预应力加固双向板的弹性分析,给出了几种常见工况的理论解,探讨了张拉体外预应力对双向板内力和变形所产生的加固作用机理。

1 体外预应力加固双向板的构造

体外预应力加固混凝土双向板的思想来自于普通混凝土梁的体外预应力加固,在具体构造上稍有不同[6,7]:首先要在混凝土板上用电锤斜向钻孔以利穿束,然后在板端浇筑高强快硬混凝土或环氧混凝土锚固块以利于安放锚具和张拉千斤顶。构造处理方式如图1所示,张拉体外预应力钢筋对双向板的作用可分解为板边弯矩和面内压力荷载的共同作用,即

其中,N0为张拉体外预应力对板边作用的板面内的等效压力荷载;M0为张拉体外预应力对双向板作用的等效板边弯矩;P为张拉控制荷载;μ为转向块与预应力钢筋之间的摩擦系数。

按受力特点可知,N0是平面力,M0是对平板的横向作用力,根据双向板受力特点可知,这2种荷载作用所产生的位移(内力)之间并没有内在联系[7,8],因此它们的作用可进行叠加计算。

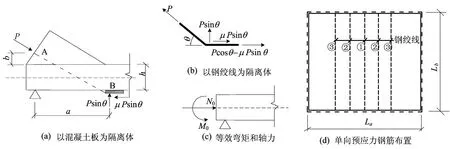
图1 体外预应力加固双向板的布置与节点构造

2 双向板在板边弯矩作用下的弹性解

2.1 双向板的弯曲变形能

双向板的微元及其内力如图2所示,自板内取一微元体hdxdy,计算当板弯曲时弯矩、和扭矩所作的功(剪力、Qy所作的功忽略不计),可得储藏在微元体内的变形能[9]:

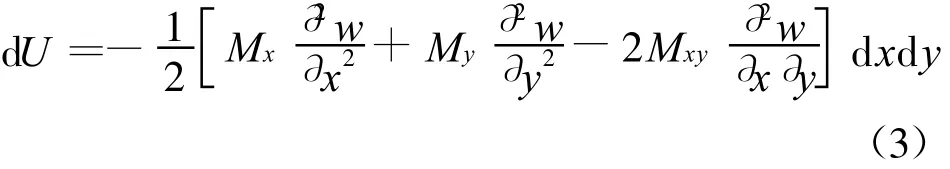
将(3)式对双向板的整个区域进行积分,即可得板的总变形能为:

图2 双向板的微元及其内力

2.2 双向板变形之虚功法的解

一个四边简支的矩形双向板沿y=0和y=b以及x=0和x=a两对边分别作用了分布弯矩M(x)、M(y),并设 M(x)、M(y)均对称于各自板边的中点,如图3所示。此时双向板的弯曲面用双重三角级数可表示为:

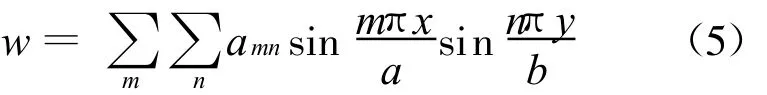
其中,amn的值可用虚功原理来求解,如将(5)式代入(4)式则得板的变形能为:

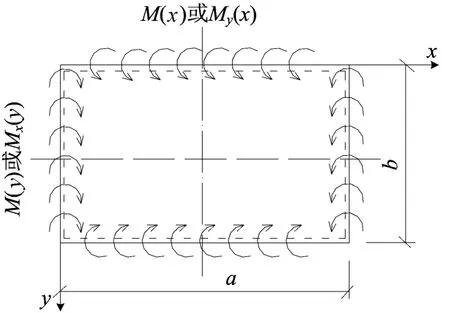
图3 两对边中点对称分布弯矩作用下的双向板

双向板的弯曲面沿 y=0,y=b,x=0,x=a 4条边上各点的斜率为:

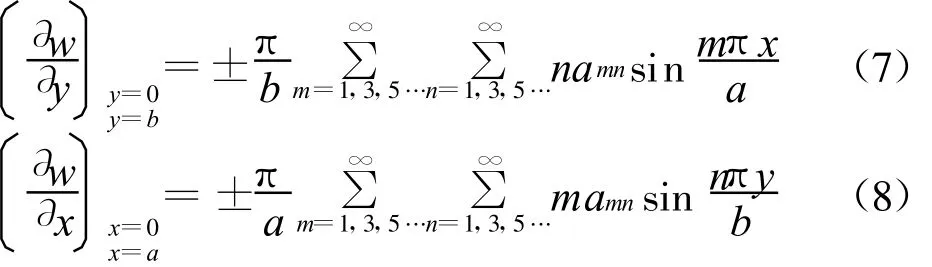
则图3中在矩形双向板的边界上分布的对称弯矩M(x)、M(y)所作的功为:

又由于:

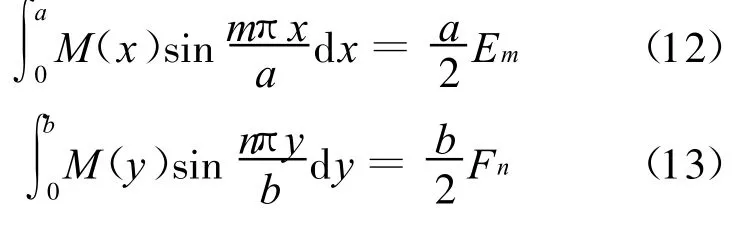
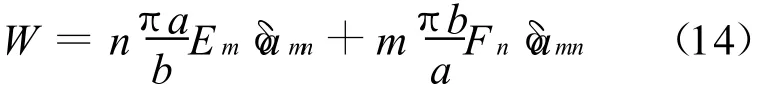
由此可得变形能的增量:

故由虚位移原理得解:

将(16)式代入(5)式即得在两对边中点对称的分布弯矩作用下双向板的挠曲面:

y向对边中点对称分布弯矩作用下的双向板,如图4所示,对于仅在y=0,y=b的两对边上作用有对称弯矩 M(x)之工况,如令=mπ b/(2a),则有解:

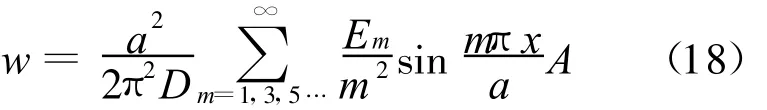
图4 y向对边中点对称分布弯矩作用下的双向板

对于两对边均布弯矩作用下的弯曲面,如当图4中作用弯矩M(x)是均匀分布的,即M(x)=,此时可求得Em=4M0/(mπ),将它代入(18)式得:

对于两对边对称集中弯矩作用下的弯曲面,如图5所示,当两对边上作用的弯矩M(x)是对称的集中弯矩M0时,此时也可得,同样代入(18)式可得:

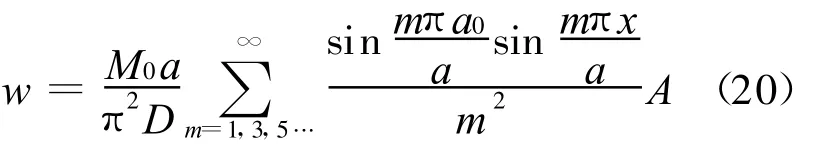
图5 y向对边对称集中弯矩作用下的双向板

3 VB程序和算例

为准确方便地得到四边简支双向板的挠度变形和内力的数值解,本文利用VB语言编制了4种常见工况下的计算程序[1],程序界面如图6所示。

图6 双向板挠度与内力计算的VB程序界面

其中,工况1为承受板面均布横向荷载q作用;工况2为承受两对边对称的均匀分布弯矩My作用;工况3为承受两对边对称的集中弯矩M0作用;工况4为承受两对边面内均布压力 Ny和板面均布横向荷载q的共同作用。

某四边简支矩形双向板的尺寸为:a×b=4 000 mm ×3 600 mm,板厚 h=100 mm,材料的弹性模量E=30 000 MPa,泊松比=0.2,分 4种荷载作用工况:

(1)承受板面均布荷载q=0.001 N/mm2;

(3)承受两对边对称的集中弯矩 M0=5 000 kN◦mm,作用位置为=2 000 mm;

(4)承受两对边面内均布压力 Ny=10 N/mm和板面均布横向荷载q共同作用。

VB程序和商用有限元软件Ansys[10]分析求解的结果对比见表1所列。

表1 双向板中点的挠度和内力

4 结束语

计算和比较表明,本文推导给出的四边简支矩形双向板在几种加固工况下挠度解的解析式是正确的。

比较工况1和工况4的结果可知,双向板的面内作用力对其在平面弯曲受力时的作用效果影响是很小的,也说明可以通过叠加法来计算它们的共同作用而无需如工况4那样进行联合求解;张拉体外预应力对板面压力荷载起到了一定的卸载作用,挠度变形和内力都得以降低,体外预应力加固双向板是有效可行的。

[1] 胡 成.钢筋混凝土双向板单向加固技术的试验研究[D].南京:东南大学土木工程学院,2006.

[2] Harajli M,Nassif H.Ex ternal prestressed members:evaluation of second order effects[J].Journal of Structural Engineering,1999,125(10):1151-1161.

[3] Virlogeux M.Non-linear analysis of externally prestressed structures[C]//Proceeding of FIP Symposium in Israel,1988:319-340.

[4] Aparicio A C,Ramos G,Casas J R.T esting of ex ternally prestressed concrete beams[J].Engineering Structures,2001,6(4):103-112.

[5] Karbhari V M,Seible F.Post-strengthening of concrete slabs[C]//Fourth International Sy mposium-FRP Reinfo rcement for RC Structures,ACI International,SP-188,Michigan,1999:575-586.

[6] 李延和.建筑结构新技术及工程实践[M].南京:河海大学出版社,2001:115-121.

[7] 黄 桥.公路钢筋混凝土简支梁桥的体外预应力加固技术[M].北京:人民交通出版社,1999:70-77.

[8] 寿楠椿.弹性薄板弯曲[M].北京:高等教育出版社,1986:49-60.

[9] 杨耀乾.平板理论[M].北京:中国铁道出版社,1980:34-36.

[10] 刘 涛,杨凤鹏.精通ANSYS[M].北京:清华大学出版社,2002:77-92.