利用函数单调性证明积分不等式

黄道增

（台州学院，浙江 台州 317000）

利用函数单调性证明积分不等式

黄道增

（台州学院，浙江 台州 317000）

积分不等式的证明方法多种多样，本文主要利用被积函数的单调性和通过构造辅助函数的单调性证明积分不等式.

函数单调性；积分不等式；辅助函数

积分不等式是微积分学中一类重要的不等式，其证明方法多种多样.如果题目条件中含“单调性”或隐含“单调性”的条件，利用函数单调性证明比较简单.本文主要讨论利用被积函数的单调性和通过构造辅助函数的单调性证明积分不等式.

1 利用被积函数的单调性

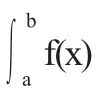
例1设f(x)为[0,1]上非负单调递减函数，

证明 由f(x)的单调递减性得：

若0＜x≤α＜1，有f(x)≥f(α)

由（1）（2）得：

2 利用辅助函数的单调性

证明方法根据——变微积分学基本定理和可导函数的一阶导数符号与单调性关系定理：

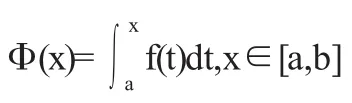
可导函数的一阶导数符号与函数单调性关系定理：设函数f(x)在[a,b]连续，在(a,b)内可导，如果在(a,b)内f'(x)≥0（或f'(x)≤0），那么f(x)在[a,b]上单调增加（或单调减少）.

证明的一般过程：

（1）构造辅助函数f(x)，取定闭区间[a,b]；

（2）求函数f(x)的导数f'(x)，再判别它的符号，利用可导函数的一阶导数符号与函数单调关系，判断函数的单调性；

（3）求函数在区间端点的函数值；

（4）根据第2步和第3步即可得证.

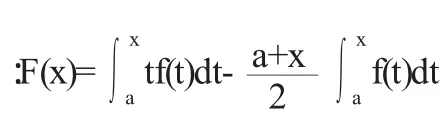
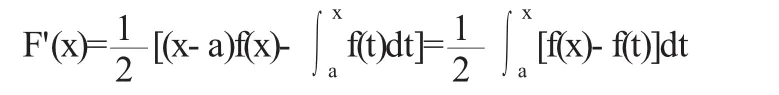
∵f(x)在[a,b]上连续，且单调增加，

∴g'(x)≥0

即g(x)在[a,b]上单调增加，

∵F(a)=0∴F(b)＞0

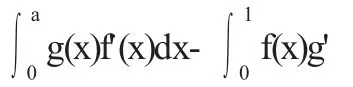
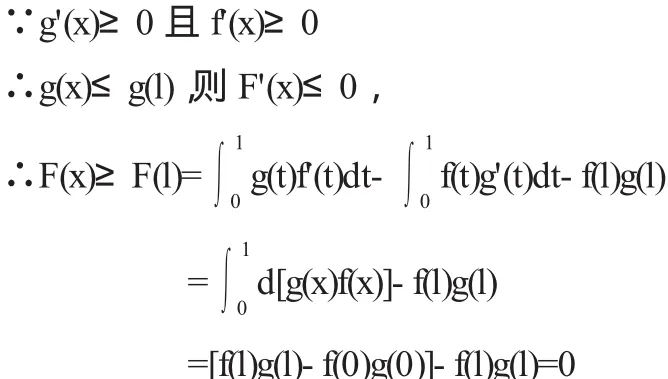
即F(x)≥0，x∈[0,1].

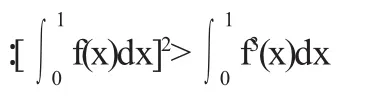
分析 可将此定积分不等式看成是数值不等式，并将常数1变为变数x，利用差式构造辅助函数.

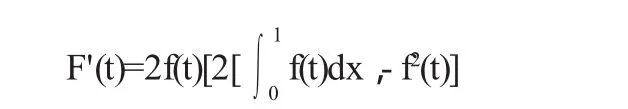
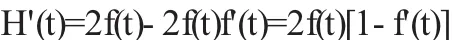
∵0＜f'(t)＜1

∴f(t)在[0,1]上严格单调递增.

∴f(t)＞f(0)=0

∴H'(t)≥0

∴对任意t∈[0,1]有H(t)≥H(0)=0，F'(t)＞0，t∈[0,1]

∴F(t)在[0,1]上严格单调递增，F(l)＞F(0)=0

〔1〕华东师范大学数学系.数学分析(上)[M].北京:高等教育出版社,2001.

〔2〕张荣.辅助函数在不等式证明中的应用[J].数学的实践与认识,2007(10).

〔3〕叶国菊，赵大方.数学分析学习与考研指导[M].北京:清华大学出版,2009.

〔4〕贾高.数学分析专题选讲[M].上海:上海交通大学出版社, 2009.

O172.2

A

1673-260X（2010）09-0014-02