基于剖面隐马氏模型的多序列比对

李成渊, 龙海侠, 孙俊, 须文波＊

(1.江南大学信息工程学院,江苏无锡 214122;2.江南大学教育学院,江苏无锡 214122)

基于剖面隐马氏模型的多序列比对

李成渊1, 龙海侠2, 孙俊1, 须文波＊1

(1.江南大学信息工程学院,江苏无锡 214122;2.江南大学教育学院,江苏无锡 214122)

多序列比对被称为NP完全问题,是生物信息中最基本的问题之一。目前,广泛使用剖面隐马尔可夫模型解决多序列比对问题。作者在粒子群优化算法的基础上,提出了将量子粒子群优化算法用于剖面隐马尔可夫模型的训练过程,进而构建了一种基于剖面隐马氏模型和量子粒子群优化算法的多序列比对算法。从核酸序列和BaliBASE比对数据库中选取了一些比对例子进行了模拟实验,并与其他算法进行了比较,结果表明,所提出的算法能在有限的时间内不仅能找到理想的隐隐马尔可夫模型,而且能得到最优的比对结果。

多序列比对;剖面隐马尔可夫模型;量子粒子群优化算法

核苷酸或氨基酸的多序列比对或联配是生物信息学中最重要、最具有挑战性的任务之一。多序列比对问题是一个将不等长的多个序列通过插入空位变成等长的过程,这些位置上的空位代表着相比对的序列从共同的祖先通过插入/删除操作的进化过程。利用多序列比对算法得到的最优比对,可用于找出蛋白质家族的模体(motifs)或保守区域(conserved domains),可用于预测蛋白质的结构和功能,也可用于进行系统发育的分析[1-2]。

目前主要有下列3种策略用于多序列比对。第一种策略是“渐进比对”策略[3-4],其基本思想是:迭代地利用两序列动态规划算法,先由两条序列的比对开始,逐渐添加新序列,直到所有序列都加入为止。第二种策略是使用随机优化算法,如模拟退火算法(SA)[5],遗传算法(GA)[6];第三种策略基于概率模型的隐马尔可夫模型[7-8]。

本研究中使用第三种策略。在多序列比对的过程中,隐马尔可夫模型主要解决3个问题:一是得分问题,二是联配问题,三是训练问题。将得分问题用来评估模型的性能,联配问题用来实现多序列的比对,训练问题用来优化模型的参数。最常用的训练隐马尔可夫模型模型的方法是基于统计和重估的方法,比如Baum-Welch算法。但是Baum-Welch算法是一个局部最优算法,使用此算法得到的最终比对结果通常远离全局最优。最近还出现了粒子群算法(PSO),此算法也是一个局部最优算法。

为了克服Baum-Welch算法和PSO算法的缺点,我们使用量子粒子群优化算法(QPSO)[9-10]来训练隐马尔可夫模型,不仅参数个数少,随机性强,并且能覆盖所有解空间,保证算法的全局收敛。

1 剖面隐马尔可夫模型的拓扑结构

图1 用于多序列比对的隐马尔可夫模型Fig.1 An example of a simple HMM of length 3 for MSA

当使用图1所示的隐马尔可夫模型进行多序列比对时,每条序列从开始到结束通过这些状态穿越模型,在这些待比对序列中进行空位字符‘-’的插入和删除操作,得到一个多序列比对结果的矩阵A=(aij)m×n,其中aij∈alph_set∪{-}。矩阵A中的每一列为一个位点上的比对,矩阵A的第i行对应参与比对的第i个序列,序列中非空字符的先后顺序在比对中保持不变。

2 基于剖面隐马尔可夫模型和QPSO的多序列比对

用量子粒子群优化算法训练剖面隐马尔可夫模型时,每一个粒子代表一个隐马尔可夫模型,通过不断的更新粒子的位置来优化隐马尔可夫模型。在训练中保持模型的长度不变,仅仅优化模型的参数:转移概率和符号发出概率。对图1所示的隐马尔可夫模型的拓扑结构,我们取待比对序列的平均值m为模型的长度,不考虑初始状态和结束状态,则模型的状态数为3m+1,状态转移概率参数为3(3m+1)个;设字符集大小为|A|,共有(2m+1) |A|个符号发出概率。所以每个粒子是维数为9m+3+(2m+1)|A|的一个实数编码串。所以DN A模型的参数个数是17m+7,蛋白质模型的参数个数是49m+23。根据转移概率和符号发出概率的性质,在对粒子对应的隐马尔可夫模型模型进行评价前,需要先对隐马尔可夫模型中的状态转移概率和符号发出概率进行归一化,以满足3m+1个转移概率归一化约束方程和2m+1个符号发出概率归一化方程。

根据粒子群算法训练的结果,得到全局最优的粒子对应的隐马尔可夫模型,接下来用此模型使用Viterbi算法进行序列的比对,得到最优的比对结果,并用基于SP(sum of pairs)打分系统的目标函数评估比对的结果。

在整个算法的过程中,根据剖面隐马尔可夫模型的拓扑结构,所使用的转移概率的形式见表1所示。

表1 转移概率Tab.1 The transition probability

2.1 模型的训练问题

2.1.1 量子粒子群优化算法(QPSO) PSO[11]是基于种群的进化搜索技术,但是所有基本和改进的PSO算法不能保证算法的全局收敛[12]。因为PSO的进化方程式使所有粒子在一个有限的样本空间中搜索。根据粒子群的基本收敛性质,受量子物理基本理论的启发,Sun等人提出了QPSO(Quantum-behaved Particle Swarm Optimization[9-10]算法是对整个PSO算法进化搜索策略的改变,进化方程中不需要速度向量,形式更简单,参数更少且更容易控制。

在QPSO算法中,粒子按照下面3个公式进行更新:

2.1.2 评估训练算法的质量 在粒子群优化算法中,需要评估每个粒子所代表的模型的质量,使用的评估函数为:

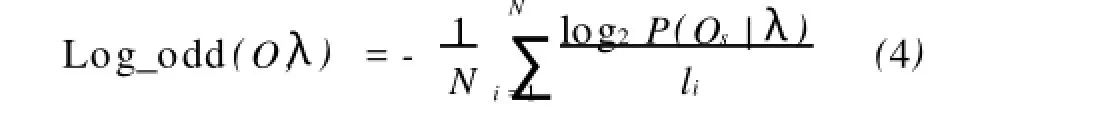
这里O={O1,O2,…,OM}是给定的待比对序列的集合,序列的个数为M个。lS是序列OS的长度。Log_odd的值越大,说明使用量子粒子群优化算法训练得到的隐马尔可夫模型,模型的参数是最优的,模型的稳定性和可靠性都较好。

2.2 模型的联配问题

2.2.1 序列联配的过程 给定3条待比对序列:O (1):A GGCT;O(2):GAACTGTA;O(3): AGCCTTA。按照下面的两个步骤可以得到序列比对的结果:

1)根据Viterbi算法和图1所示的隐马尔可夫模型拓扑结构找出每条序列所对应的状态序列,如图2所示,每条序列的氨基酸碱基对应一个匹配状态或一个插入状态。

图2 每条序列所对应的状态序列Fig.2 Each sequence corresponding to the state sequence

由图3生成的状态序列,我们可以进行空位字符‘—’的插入操作,见图3。所有的序列中与匹配状态M相对应的氨基酸碱基是比对的,这些氨基酸碱基位于同一列;与插入状态Ik相对应的氨基酸碱基位于Mk-1或DK-1之后,Mk或DK之前。

图3 空位字符‘-’的插入Fig.3 Insert the gap characters’-’

由步骤(1)和步骤(2),得到联配后的序列为图4所示。

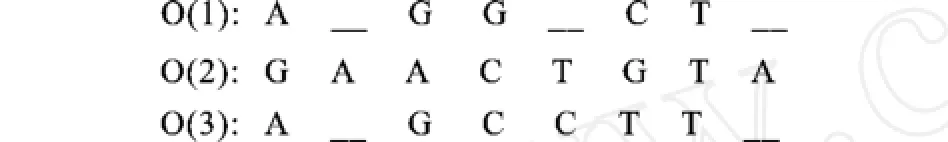
图4 联配后的序列Fig.4 Aligned sequences

2.2.2 评估比对序列的质量在利用Viterrbi算法获得的路径进行比对后,需要通过基于SP(sum of pairs)打分系统的目标函数[13]对比对结果进行评估。我们使用下面标准的sum-of-pairs打分函数:

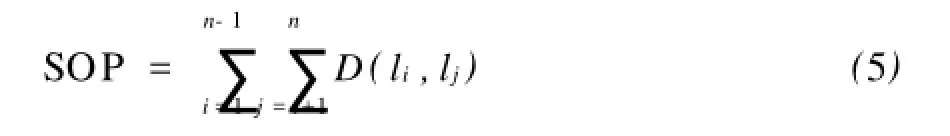
这里,li是已比对的序列,D为距离矩阵.

为了避免在比对过程中空位的积聚,我们从SOP分数中推演出仿射几何学的空位代价,对于比对结果中一条序列的空位代价按照下面的公式进行计算:

这里GOP表示第一个开口空位的固定罚分, GEP表示对于扩展的空位的罚分,n为一条序列中空位的个数。对于已比对的每条序列的空位都要计算相应的空位代价。多序列比对结果的SOP的分值减去空位代价的总和,即为SOP的分值。

3 实验结果

3.1 实验数据

3.1.1 数据集1(模拟的核苷酸序列) 使用软件Rose[8]软件产生如下的核酸序列:“low-short”“low-long”,“high-short”,和“high-long”.

3.1.2 数据集2(Pfam数据库中的3个蛋白质家族) 3个蛋白质家族分别为G5,CagY_M and Interferon,它们来自Pfam数据库[14],见表2。为了避免隐马尔可夫模型模型中的过拟合,分别把3个蛋白质家族分成训练集和测试集。

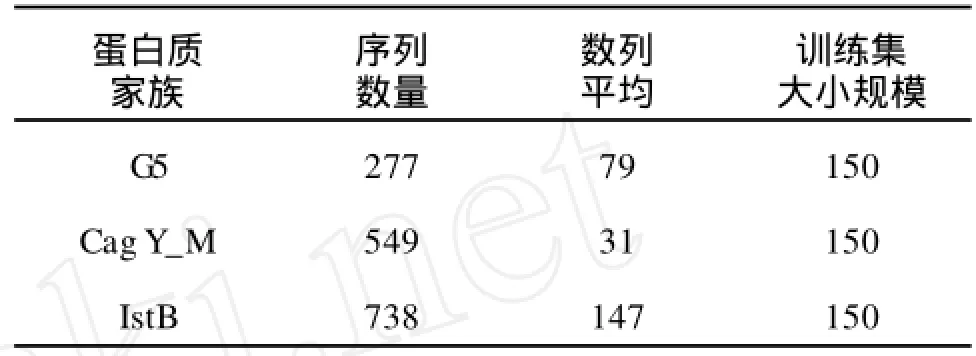
表2 蛋白质家族N:序列的个数,LSEQ:数列的平均,T:训练集的大小Tab.2 Protein familiesN:the number of sequences LSEQ:the average of seriesT:The size of training sets

3.2 实验设置

实验中,我们使用均匀分布初始化所有的种群;分别使用了Baum-Welch(BW)、Particle Swarm Optimization(PSO)、Quantum-behavedParticle Swarm Optimization(QPSO)3种算法训练隐马尔可夫模型,用Log_odd目标函数来评估4种训练算法的性能,并且使用SOP打分系统的目标函数来评估比对效果。每种算法分别迭代1 000次,共进行了20次模拟实验。

对于PSO算法,使用如下的参数:种群数=20;惯性权重(ω)从1.0到0.5线性减少;c1=c2=2.0最大速度(v→max=1.0

对于QPSO算法使用如下的参数:种群大小= 20;收缩扩张系数,从1.0到0.5线性减少;并且,在SOP打分函数中,核酸和蛋白质分别使用下面的打分矩阵、空位开放和空位扩充。

1)对于核酸序列,使用ClustalW 1.81的“swgap”置换分数表,空位开放和空位扩充分别为15、7。

2)对于蛋白质序列,使用BLOSUM62打分矩阵,空位开放和空位扩充分别为11、2[9]。

3.3 实验结果

表3给出了核酸序列的结果,这里是以Logodd score作为目标函数,用来评估训练隐马尔可夫模型的质量,从表中可以看出,QPSO取得了最好的平均值,PSO算法的结果和BW算法的结果相当,在Low-long序列和High-long序列上的结果不如BW得出的结果好,可以说明,PSO算法随着序列个数的增加效果不如BW的效果好。

表4也给出了核酸序列的结果,这里是以SOP score作为目标函数,用来评估核酸序列的比对的效果。从表4可以看出,QPSO优于其他所有的算法,其次为CW工具得出的比对结果优于BW和PSO算法得出的结果,PSO算法也是一种局部最优算法,对BW算法没有多大的改进。

表3 隐马尔可夫模型得到的核酸序列的Log_odd scores平均值和方差Tab.3 HMM log-odds scores±standard error of Nucleotidesequences

表5～8概述了3个蛋白质家族的隐马尔可夫模型训练和序列比对的结果。表5和表6分别给出了训练集的最优的Log-odd scores和SOP scores的平均值和方差,表7和表8分别给出了评估集的最优的Log-odd scores和SOP scores的平均值和方差。从4个表中,可以看出,对于蛋白质家族,无论是在训练集还是评估集上,QPSO算法在模型的训练上和比对的效果上都优于BW和PSO算法。

表4 核酸序列比对结果的SOP平均值和方差Tab.4 SOP scores for the final alignments of Nucleotide sequences

表5 隐马尔可夫模型得到的蛋白质序列训练集的Log_odd scores平均值和方差Tab.5 HMM log-odds scores±standard error for the training sets of three protein families

表6 蛋白质序列训练集的最优的SOP scores的平均值和方差Tab.6 SOP scores for the final alignments of the training sets of three protein families

表7 隐马尔可夫模型得到的蛋白质序列测试集的Log_odd scores平均值和方差Tab.7 HMM log-odds scores±standard error for the validation sets of three protein families

表8 蛋白质序列测试集的最优的SOP scores的平均值和方差Tab.8 SOP scores for the final alignments of the validation sets of three protein families

图5、6、7刻画了以Log-odd score作为目标函数,算法分别运行20次得到的核酸序列和蛋白质序列的平均值的收敛过程。

图5 Low-short核酸序列的Log-odd平均分数Fig.5 Mean Log-odds scores for Low-short Nucleotide

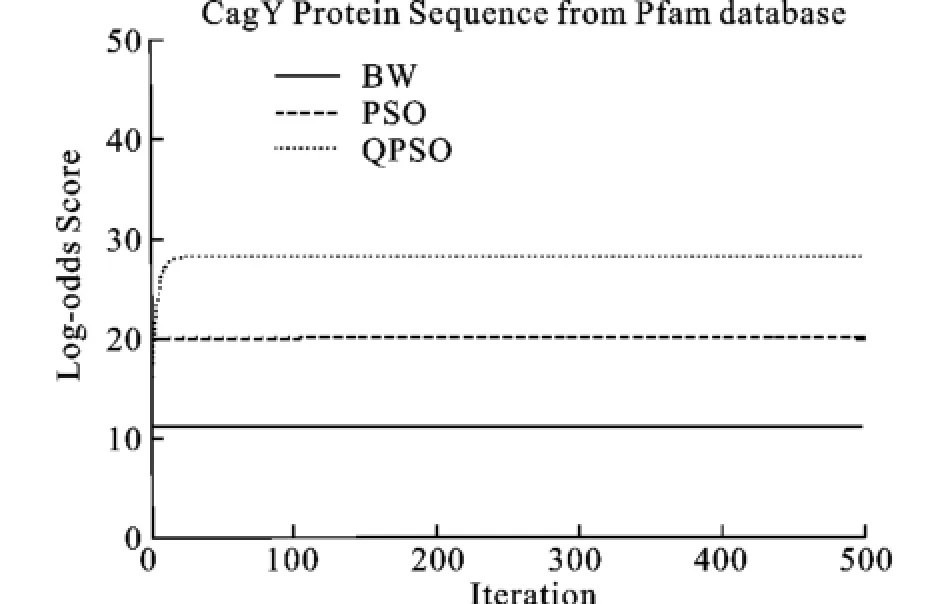
图6 Cag_Y蛋白质序列的Log_odd平均分数Fig.6 Mean Log-odds scores for training sets of CagY_ M protein family

图7 Interferon蛋白质序列的Log_odd平均分数Fig.7 Mean Log-odds scores for validation sets of Interferon protein family

从图中看出,QPSO性能最好,在迭代的最后得到的Log-odd score的分值也最好,除了图9, PSO算法的性能优于BW算法。从收敛速度上看, BW和PSO的收敛速度最快,其次为QPSO算法,但是QPSO算法在迭代进行到一半的时候,Logodd score的值就已经超过PSO算法和BW算法,并且在整个运行过程中,QPSO都在不断的提高自身的性能,而PSO算法和BW算法已经早早地收敛了。

图8 Low-short核酸序列的SOP平均分数Fig.8 Mean SOP scores for Low-short Nucleotide

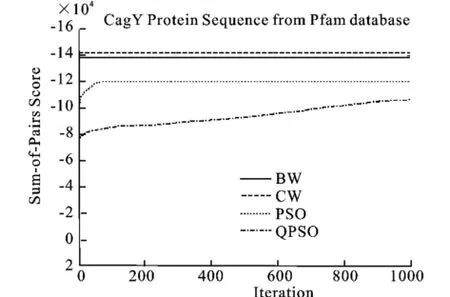
图9 Cag_Y蛋白质序列的SOP平均分数Fig.9 Mean SOP scores for training sets of CagY_M protein family

图10 Interferon蛋白质序列的SOP平均分数Fig.10 Mean SOP scores for validation sets of Interferon protein family

图8、9、10表明了以SOP score作为目标函数,算法分别运行20次得到的核酸序列和蛋白质序列的平均值的收敛过程。收敛情况与上述情况相同。

4 结 语

提出了使用QPSO算法来训练剖面隐马尔可夫模型的参数,进行多序列的比对.从实验结果可以看出,以Log-odd score作为目标函数,QPSO算法相比BW算法和PSO算法,是一种非常有效的训练HMM模型模型的方法。并且从实验结果还可以得出,以SOP作为目标函数,QPSO比其他所有的方法而言,能产生较好的比对结果。这是因为QPSO算法是一种全局收敛算法,并且需要调整的参数也比较少。

在计算时间上,QPSO消耗的时间和PSO消耗的时间相当,远远大于BW算法的运行时间。平均来说,QPSO和PSO的运行时间为6小时,BW的运行时间为5小时.并且,随着序列个数和序列长度的增加,QPSO消耗的时间也随着增大。

在进一步的研究工作中,我们将进一步改善QPSO算法,来提高HMM的性能,减少序列比对的时间。

[1]GUAN Wei-hong,X Z-Y,ZHU Ping.Nonlinear prediction analysis of properties in protein sequences(Ⅰ)[J].Journal of Food Science and Biotechnology,2008,27(1):71-75.

[2]GUAN Wei-hong,X.Z.-Y.,ZHU Ping.Nonlinear prediction analysis of properties in protein sequences(Ⅱ)[J].Journal of Food Science and Biotechnology,2008,27(2):103-105.

[3]Thompson J D,Higgins D G,Gibson T J.CLUSTAL W:improving the sensitivity of progressive multiple sequence alignment through sequence weighting,position-specific gap penalties and weight matrix choice[J].Nucl Acids Res,1994, 22(22):4673-4680.

[4]Feng D F,Doolittle R.Progressive sequence alignment as a prerequisitetto correct phylogenetic trees[J].Journal of Molecular Evolution,1987,25(4):351-360.

[5]Kim J,Pramanik S,Chung M J.Multiple sequence alignment using simulated annealing[J].Comput Appl Biosci,1994, 10(4):419-426.

[6]E Jung Lee,S F S,Chen-Chia Chuang,et al.Genetic algorithm with ant colony optimization(GA-ACO)for multiple sequence alignment[J].Applied Soft Computing,2008,8(1):15-17.

[7]Mamitsuka H.Finding the biologically optimal alignment of multiple sequences[J].Artif Intell Med,2005,35(1-2):9-18.

[8]Loytynoja A,Milinkovitch M C.A hidden Markov model for progressive multiple alignment[J].Bioinformatics,2003, 19(12):1505-1513.

[9]Jun S,Wenbo X,Bin F.In A global search strategy of quantum-behaved particle swarm optimization[J].Cybernetics and Intelligent Systems,2004,321:325-331.

[10]Jun S,Bin F,Wenbo X.In Particle swarm optimization with particles having quantum behavior[J].Evolutionary Computation,2004,321:325-331.

[11]Kennedy J,Eberhart R.In Particle swarm optimization[J].Neural Networks,1995,1994:1942-1948.

[12]Clerc M,Kennedy J.The particle swarm-explosion,stability,and convergence in a multidimensional complex space[J]. Evolutionary Computation,2002,6(1):58-73.

[13]Thompson J D,Plewniak F,Poch O.A comprehensive comparison of multiple sequence alignment programs[J].Nucleic Acids Res,1999,27(13):2682-2690.

[14]Sonnhammer E L,Eddy S R,Durbin R.Pfam:a comprehensive database of protein domain families based on seed alignments[J].Proteins,1997,28(3):405-420.

(责任编辑:李春丽)

Multiple Sequence Alignment Based On the Profile Hidden Markov Model

LI Cheng-yuan1, LONG Hai-xia2, SUN Jun1, XU Wen-bo＊1
(1.School of Information Technology,Jiangnan University,Wuxi 214122,China;2.School of Education,Jiangnan University,Wuxi 214122,China)

Multiple sequence alignment(MSA),known as NP-complete problem,is one of the basic problems in computational biology.At present Profile Hidden Markov Model(HMM)was widely used in multiple sequence alignment.This manuscript presented the quantum-behaved particle swarm optimization(QPSO)which was based on particle swarm optimization.The proposed algorithm was used to optimize the profileHMM.Furthermore,an integration algorithm based on the profile HMM and QPSO for the MSA was constructed.Then the approach was evaluated by a set of standard instances which are chosen from nucleotides sequences and the benchmark alignment database,name as BAliBASE.Finally our results are compared with other algorithms.The result shown that the proposed algorithm not only finds out the perfect profile HMM,but also obtains the optimal alignment of multiple sequence.

multiple sequence alignment,profile hidden markov model,quantum-behaved particle swarm optimization

Q 811.4

:A

1673-1689(2010)04-0634-07

2009-08-07

李成渊(1980-),男,江苏无锡人,生物信息学博士研究生。Email:lichengyuaning@gmail.com

＊通信作者:须文波(1946-),男,江苏无锡人,教授,博士生导师,主要从事生物信息学方面的研究。Email:xwb_sytu@hotmail.com