基于Vague集记分函数法的模糊插值算法

张 韬,徐芸芸,李赞成,林振荣

(1.空军工程大学工程学院,陕西西安 710038;2.徐州空军学院机场工程系,江苏徐州 221000;3.徐州空军学院油料物资系,江苏徐州 221000)

0 引言

利用探测仪器对目标进行探测时,往往需要对探测数据进行成像处理。由于采集的数据均为离散分布,不可能得到所有成像网格点上的数据,因此必须要对采集的数据进行插值计算,才能得到针对每个成像网格点的数据。

现有的离散数据插值加权运算方法能够根据已知点与未知点的距离进行加权运算[1],在运算时存在的主要问题有:1)不能保证均匀取值,且增加运算量;2)考虑到梯度变化的情况,尤其是发生突变时,不能保证插值的准确性。

Vague集是由Gau和Buehrer[2]于1993年提出的。由于同时考虑隶属与非隶属两方面的影响,其决策时的合理性较之传统的模糊集更强。本文通过分析现有插值加权算法,将基于Vague集[2-3]的记分函数法应用到插值计算中,以得到更准确的网格点插值。

1 现有的插值加权算法

1.1 按距离加权平均算法

对于离散点数据进行插值运算一般采用的方法是按距离加权平均法。该算法的基本思想如下:

假定已知数据点值对网格点值的影响与距离有关,其基本原则是越靠近网格点的已知数据点值对网格数据点值的影响越大。影响程度可用一个权系数来量化,权系数的大小取已知数据点到网格数据点的距离的倒数,对已知数据点值进行加权即得到未知网格点的数值。

以图1为例,其中 A点为未知网格点,B,C,D等点为已知数据点,各已知点距离 A点的距离为d IA,以 B点为例,有:

由已知各点的探测值及与A点的距离,即可求出A点的内插值Z A为:

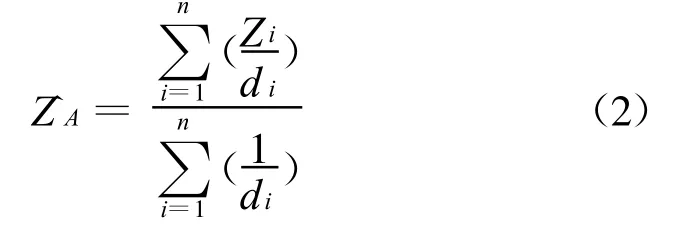
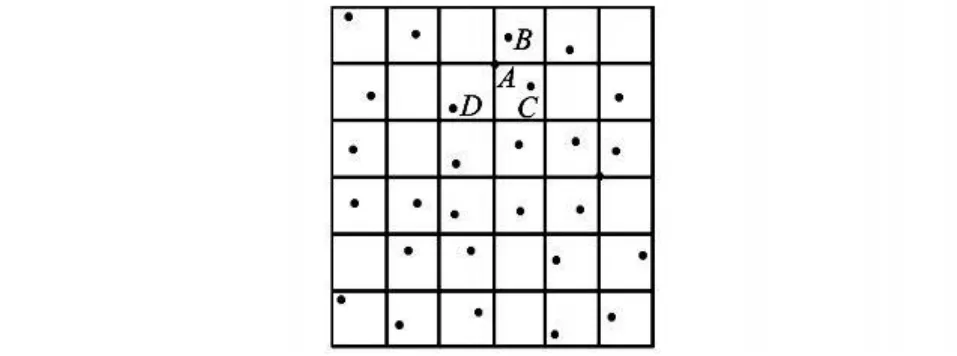
图1 按距离加权平均法插值示意图Fig.1 Interpolation calculation based on the distance weighted mean

1.2 按方位取点加权算法

该方法能根据按距离加权平均算法存在的问题进行修正,提出了按方位取点加权的计算方法。其基本思路如下[1]:

仍对A点进行插值计算,先以A点为中心把平面分为4个象限,再将象限等分为n份,则得到A点的插值表达式为:

其中,

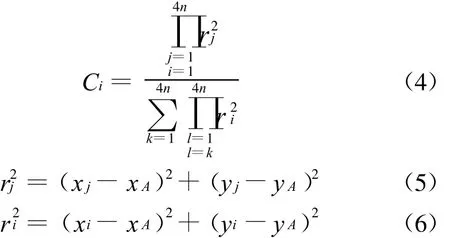
且有系数Ci满足:

其算法的基本步骤为:

1)输入原始数据点;

2)确定插值点平面坐标;

3)在各个区域中分别寻找距离插值点最近的点,求出之间的距离;

4)利用式(3)与式(2)计算各插值点的值;

5)重复以上步骤,求出所有插值点的值。

2 现有算法的缺陷

仍以图1中A点为例,则上述两种距离加权平均法的缺陷具体体现在:

1)利用第一种算法计算时,存在的主要问题是如果已知数据点大部分集中在A点的一侧,而不是较为均匀地分布在 A点周围,则必然会增加插值误差。而且不加选择地对A点所有邻近点进行计算也会大大增加计算量。

2)以上两种方法均没有考虑到探测数据突变情况的存在,即没有考虑梯度突变情况的存在。例如,在实际处理中可能会存在两个已知数据点与A点距离相差不大,但探测数据值却相差很大的情况。因此,一味采用距离平均值作加权因子同样也会增大插值估算的误差。

3 基于Vague集的模糊插值算法(VFIA)

针对以上两种插值算法的缺陷,本文通过应用目前在模糊多准则决策方面应用较为广泛的基于Vague集记分函数法,提出了一种对插值进行模糊加权计算的方法。

3.1 基于Vague集的记分函数法

Vague集的提出是通过对Zadeh的模糊集进行扩展与延伸,从而增强了模糊多准则决策的科学性与合理性。Vague集应用于模糊多目标决策的最大特点是同时考虑隶属与非隶属两方面的信息,这使得Vague集在处理不确定性信息时比传统的模糊集有更强的表示能力,且具备更强的灵活性。

设论域X={x1,x2,…,xn},其中元素x i(i=1,2,…,n)是所讨论的对象。X上一Vague集A由真隶属函数tA和假隶属函数fA按下面公式进行描述:

式中,t A(xi)是由支持xi的证据的肯定隶属度的下界,f A(xi)则是由反对xi的证据的否定隶属度的下界,且tA(xi)+fA(xi)≤1。

在利用Vague集进行模糊决策过程时,Chen和Tan[4]于1994年提出了用记分函数S表示决策目标满足决策者要求的程度。采用如下公式计算:

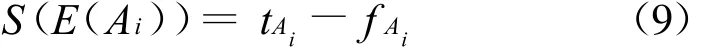
式中,S(E(Ai))的值越大,表明目标Ai越满足决策者的要求。

在后续的发展中,李凡等用例子阐明式(8)的不足之后,给出的方法是定义以下两个记分函数S1和S2[5]:

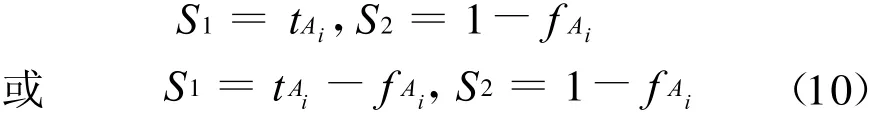
式中,S1与S2分别表示目标Ai适合和不适合决策者要求的程度。决策规则为:先根据S1的值进行选择,该值越大,则目标Ai越适合决策要求;当S1的值相同时,再根据函数S2的值进行选择,该值越大,则目标Ai越适合决策要求。

文献[6]证明,通过对弃权人群进行分析,可更合理地进行决策。文献[6]通过定义如下的记分函数:

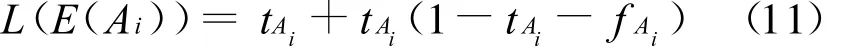
表示决策方案 Ai满足决策者要求的程度。L(E(Ai))的值越大,表示目标越满足决策者要求。

文献[7]中,还提出了一种更加完善的计算方法,从而确保了利用Vague集记分函数法一定可以得到排序结果。下面将采用基于Vague集的记分函数法对未知网格点插值问题进行计算。

3.2 基于Vague集的模糊插值算法

针对上文中提到的缺陷1),首先引用按方位取点加权的计算方法将未知点A周围的空间分为4个象限。之后,将每个象限均分为相等的n个区域,在每个区域中寻找与A点最近的已知点,再通过计算每个最近已知点与A点的距离d进行加权求和。

显然,在每个象限中均可以得到一个关于 A点的插值:

在第j个象限中,有:

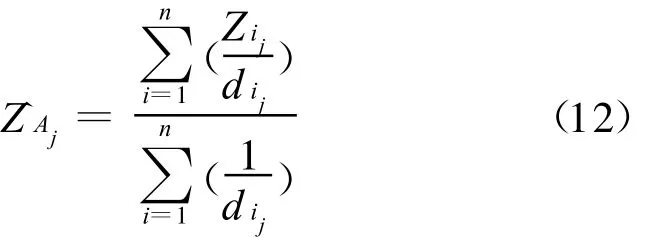
式中,i=1,2,…,n;j=1,2,…,4。

显然,一般情况下由4个象限的探测数据分别得到的插值能够完全相同的机率是很小的。通常情况下,如果由4个象限分别计算得到的插值相差不大时,求得4个象限的插值的平均值可以作为一个较为合理的选择。但必须考虑到在不同象限中探测数据有可能发生突变的情况,这里引入反映插值梯度变化的隶属度函数来对各象限插值进行模糊计算。

为凸显梯度的变化情况,确保由各相邻点得到的插值最大限度地接近真实值,论文利用模糊数学中基于Vague集记分函数法来处理各象限的插值估算问题。

1)真隶属度的定义

定义1:利用第j个象限中最近相邻探测点K定义该象限插值^Z Aj的真隶属度为:

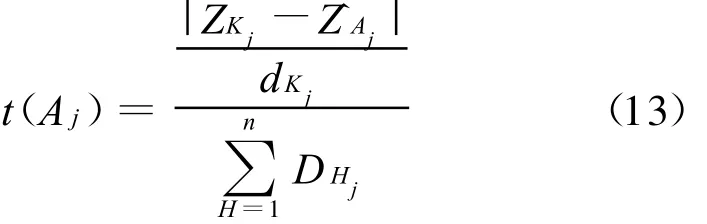
式中,K点为距离A点最近的相邻点。D Hj为第j个象限中各等份中相邻点与利用式(2)得到的A点插值的差与距离的比。即:

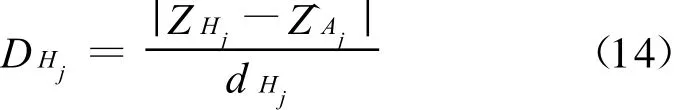
显然,该隶属度利用相邻最近已知点与插值点的变化率情况反映了插值点插值的梯度变化情况。

2)假隶属度的定义

定义2:利用第j个象限中最远相邻探测点L定义该象限插值^ZAj的假隶属度为:

利用Vague集的记分函数法,可以得到第 j象限的插值隶属度为:

分别求出4个象限的μj,即可分别求出4个象限A点的模糊加权插值。

计算出4个象限的模糊加权插值后,即可求出A点的最终插值:

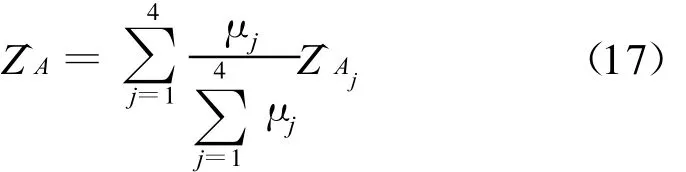
显然,通过利用基于Vague集的记分函数法,得到的插值要比直接采用加权平均法进行计算要合理。

3.3 VFIA算法总结

对算法的计算步骤总结如下:

1)将未知网格点的4个象限划分为n等份;

2)分别求出未知网格点在4个象限的插值;

3)分别计算出4个象限的真假隶属度值;

4)利用基于Vague集的记分函数法,计算出每个象限的记分函数;

5)由4个象限的计算结果,求出最终的未知网格点插值。

4 实验应用

利用VFIA算法,对地下目标探测进行数据处理实验。实验时采用TEM探测仪器进行地下目标探测,得到各个测线的电阻率,首先利用已知点对每一列未知像素点进行插值计算;之后再对每一行未知像素点进行插值计算,这样即可实现对地下目标的切面建模。通过建立函数关系,将电阻率转换为256级灰度处理,可得到探测数据关于各个切面的图像。下图为采用加权平均法及VFIF算法分别得到的水平切面图像。

图2 加权平均法得到的水平切面图像Fig.2 Horizontal section map based on the distance weighted mean

图3 VFIA算法得到的水平切面图像Fig.3 Horizontal section map based on the VFIA Calculation

由图像对比情况可以看出,由VFIA算法得到的图像由于利用Vague集进行计算,考虑到各个象限最近点取值情况,因此其纹理更加丰富,反映出图像的细节变化也更多。

5 结论

通过分析现有插值算法,提出了一种基于Vague集记分函数法的模糊插值算法,并通过实验进行了对比验证。主要结论如下:

1)新算法考虑到了未知点周围4个象限中已知点的取值情况;

2)新算法能有效缩减普通插值运算计算量;

3)由于在计算时充分考虑了梯度的变化情况,从而确保了插值的准确性,也使得图像的细节变化能够准确体现。

研究结果成功地应用到了文献[8]中的地下金属小目标探测成像处理过程。

[1]周旭.基于 VRM L的 TEM解释数据三维可视化研究[D].长春:吉林大学,2005.

[2]Gau W L,Buehrer D J.Vague sets[J].IEEE Trans on Systems,Man and Cybernetics,1993,23(2):610-614.

[3]Fuller R,Carlsson C.Fuzzy multiple criteria decision making:recent developments[J].Fuzzy Sets and Systems,1996,78:139-153.

[4]Chen S M,Tan J M.Handling multi-criteria fuzzy decision-making problems based on vague set theory[J].Fuzzy Sets and Systems,1994,67(2):163-172.

[5]李凡,卢安,蔡立晶.基于 Vague集的多目标模糊决策方法[J].华中科技大学学报,2001,29(7):1-3.LI Fan,LU An,CAI Lijin.Multicriteria decision making based on vague set[J].Journal of Huazhong University of Science and Technology,2001,29(7):1-3.

[6]刘华文.多目标模糊决策的Vague集方法[J].系统工程理论与实践,2004,24(5):103-109.LIU Huawen.Vague set methods of multicriteria fuzzy decision making[J].Systems Engineering-Theory &Practice,2004,24(5):103-109.

[7]张韬,陆廷金,马建军.基于 Vague集模糊多准则决策记分函数法改进性探讨[J].系统工程,2006,24(7):120-123.ZHANG Tao,LU Tingjin,MA Jianjun.Discussion on improvement of score function methods based on vague sets for fuzzy multi-criteria decision-making[J].System Engineering,2006,24(7):120-123.

[8]张韬,陆廷金,马建军,等.瞬变电磁法在地下金属物体探测中的应用[J].弹箭与制导学报,2006(3):293-295.ZHANG Tao,LU Tingjin,MA Jianjun,et al.The application of transient electromagnetic method in detection of underground metal object[J].Journal of Projectiles,Rockets,Missiles and Guidance,2006(3):293-295.