基于时频面霍夫变换的谐波族检测算法
2010-08-27唐玉志
唐玉志,刘 瑜,郭 艳,吴 娜
(1.西北工业大学,陕西西安 710072;2.西北核技术研究所,陕西西安 710024)
0 引言
直升机和无人机在现代战争中发挥着重要作用,可用于战场的监视、运输、攻击等,反潜直升机等配备的声纳系统的性能逐渐升级,对潜艇的威胁也越来越大。对直升机(包括螺旋桨驱动的反潜机)和无人机的探测和预警,是一项重要的战术任务。低成本、可靠、探测距离远、布设方便的探测系统,部分国家已有设备正式列装,其性能也在持续提高中。
直升机和大部分的无人机等由螺旋桨驱动,其发出的噪声信号包含有一组或多组谐波信号,每一组谐波信号的谱线在频域上呈等间隔分布,强度处于同一量级。将具有这种谐波关系的一组信号称为谐波族信号(harmonic signal set)。在由声学方法进行直升机等目标的探测时,以往多据其能量最高的谱线或者频谱的整体形状提取特征,结合模式识别算法进行检测[1-5]。这类算法往往没有有效利用其谐波性质,在强干扰或噪声背景下检测能力大幅降低。
本文使用谐波小波变换方法求得含噪声谐波族信号(以模拟直升机和无人机等的谐波族信号)的时频分布,在此基础上进行Hough变换,基于频率分集技术[6-8]中信号融合处理技术构建检测量,并在给出检测结果的同时,给出谐波族的基频及其变化率。
1 信号的时频分布及Hough变换
1.1 基于谐波小波的时频分布
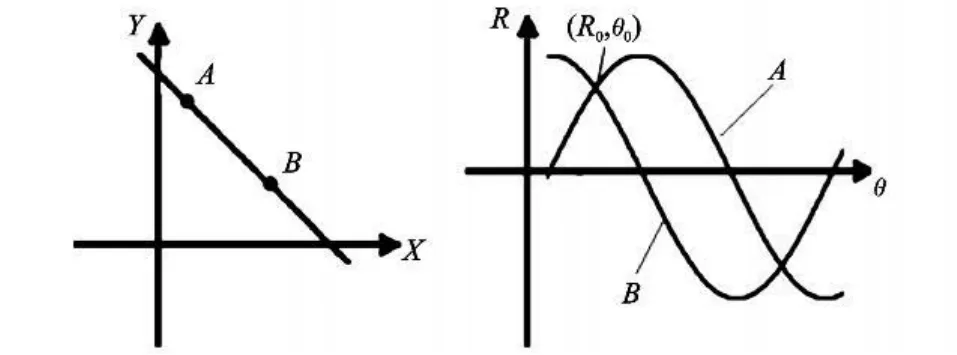
频率范围为m~n Hz(m,n为实数,且0 式(1)表示的是一个强度在m ~n Hz范围内为单位幅度的谐波小波。对于复信号 x(τ),加时间窗win(τ)以改善时间定位能力,其谐波小波变换系数为[10-11]: hwt(m,n,t)代表了x(τ)与谐波小波w(t)的相关程度。hwt(m,n,t)2可作为信号在该带宽范围内能量的量度。在选定的时间和频率范围内变化(m,n,t)的组合,将 hwt(m,n,t)2排列在二维时频平面上,即得到x(τ)的一个时频分布[12-13],该二维平面即称为时频面。 设有二维笛卡尔坐标系下的两点 A(x,y)和B(x′,y′)。过两点的直线为 AB,过原点的垂线长度为R,与横坐标Ox的夹角为θ。过AB两点的直线可以表示成y=kx+b,有: 代入直线AB的表达式,可以得到 图1 Hough变换示意图,(左为图像空间,右为参数空间)Fig.1 Illustration of Hough transformation(lef t one is the image domain,right one is the parameter domian) 对于固定的点 A(x,y),当参数(R,θ)变化时,其轨迹为一条曲线,每一点代表了过点 A(x,y)的一条直线的R和θ。假设曲线上与直线AB相对应的点设为(R0,θ0),则直线 AB上所有点在参数空间的曲线都将通过点(R0,θ0),经加权后必然在点(R0,θ0)处形成极大值。通过适当的搜索算法可找出极值点(R0,θ0),它唯一的定义了直线 AB并可直接得到其截距和斜率。 将使用谐波小波变换得到的信号时频分布作为Hough变换的二维输入图形,以强度为变换域中各点的加权值。直升机、无人机等目标的谐波族噪声包含多条谱线,在时频面上,表现为多条直线,经Hough变换以后,参数空间中出现多个极值点。极值点的个数对应于谐波信号的阶数。 设谐波族信号基频为 f 1(t),最高阶数K,第n阶谐波频率f n(t),n=1,2,…,K。时频分布像元数为M×N,时间和频率分辨率分别为Δt和Δf。以时间中心和频率0作为时频分布的坐标原点,时频分布都位于上半平面。 在直升机等目标飞行平稳、且没有多普勒效应时,噪声谱线频率不随时间变化,时频图中各阶谐波时频线的斜率为0,在参数空间(R,θ)中,有: (式中,θn为第n阶谐波对应谱线的垂线与纵轴的夹应的(Rn,θn)各点等间距分布在纵坐标轴线上。 谐波族信号频率变化时,在某一时间长度内,可认为信号频率是接近于线性变化的,变化率频率的时变由多普勒示目标与测点的径向相对速度。谐波谱线成为斜率与阶数成正比的一组直线,其斜率为: 可在时频分布计算中合理选择参数,使得k′n=tan(θn)≅θn近似成立,则在Hough变换的参数空间(R,θ)中,θn落在一系列等间隔的点上。 [89]Maung Aung Myoe, In the Name of Pauk-Phaw: Myanmar’s China Policy Since 1948, Singapore: Institute of Southeast Asian Studies, 2011, p.190. 各阶谐波谱线的垂线与纵轴的夹角分别为:θn,n=1,2,…,K 。在t=0的时刻,有 f 1=f 2/2=f 3/3=…,由几何关系有:Rn=f n cosθn。理论上,参数空间(R,θ)中R的分布不再是等间距的。但当谐波族信号频率变化率较低,k′n=tanθn≅θn成立时,也有cosθn≈1成立。这时有:Rn=nf 1,分布成为等间距的。Hough变换中,Δt和Δf本身就有一定宽度,该近似带来的误差不致引起极值点大的偏移。 因此,在时频面上谱线斜率较小的情况下,各阶谱线在参数空间(R,θ)中对应的点就散布在一条直线附近。这条直线过参数空间的零点,可以表示为: 式中: 图2 频率时变谐波信号的时频分布与Hough变换参数的示意图Fig.2 Time-frequency distribution of frequency-shifting signal and parameter of the Hough transformation 式(7)中的k是Hough变换参数空间中多个极值点拟合为一条直线时的斜率,是一个平均值,用于进行谐波信号频率变化率的计算时,可以得到比利用单一谱线更好的计算结果。 由2.2节,要得到谐波基频,需要先在(R,θ)空间的上半平面,即在射线与 R轴的角度 ψ∈取不同值的射线上进行搜。 对于某一确定的ψ,射线上各点的幅度表示了时频面上各点经Hough变换给予的能量的总贡献。设射线上离散点总数为M 0个,第m个点的能量为p m,m=1,2,…,M 0。定义射线上的总能量Eψ和熵函数Sψ分别为: 熵函数Sψ具有以下性质: 3)当p m的分布位于以上两种情况之间时,0 在确定ψ,从而确定了信号中各阶谐波在参数空间中所在的射线以后,就可以在此射线上搜索谐波信号基频的确切位置。在射线上定义函数: K为谐波族中的最高阶数。使Pm取得最大值的点,就是谐波族信号基频的时频线在参数空间(R,θ)中的映射,据此可进一步由式(5)和式(6)得到目标的部分运动学参量。 在无线通讯领域,由于电磁波在传输过程中的多途随机衰落,导致信息在某些时刻不能准确检测。现常采取频率分集的方法,将信息在多个载频上同时发送,在检测端采取某种融合方式将这些频率携带的信息经综合后解码,避免了单一频率的随机衰落引起的信息丢失。 直升机或无人机噪声为谐波族信号。Pm反映了谐波族信号中各阶分量的贡献的和,将其用于对目标的检测,可以得到比基于某单个频率分量更好的检测结果。Pm实际就是频率分集技术中各频率贡献以等增益方式融合的结果。 Hough变换和参数空间中ψ的搜索算法计算量很大。为节省计算时间,可以先在时频面上每一个时刻的谱分布上应用式(9)的谐波基频搜索算法,将结果重新排列成一个关于t和基频m的时频面,其频率范围缩小为基频可能的取值范围。再将此时频面进行Hough变换,找出极值点,就可以得到信号基频的参数。经这样变换,可以使得Hough变换的计算量大幅降低为原来的1/K,并且在参数空间(R,θ)中只需要搜索极值点,而不需要进行一次二维搜索和一次一维搜索。 在Hough变换的参数空间(R,θ)中,若网格划分的较细密,则时频面上某一点变换后对应的分布区域将减少,时频面上的直线在参数空间中对应点的能量将更加集中,幅度更高,有利于进行检测,也可以更加准确地定位基频和频率变化率。 网格加密带来的代价是计算量的增加。 图3中是两组平稳谐波族信号的时频分布、Hough变换和据式(9)的基频搜索结果。谐波族信号的基频为10 Hz,最高阶数6。时频面中,Δt=1/15 s,Δf=0.2 Hz,Hough变换网格数500×500,θ范围为-π/4~π/4。图中上面一组是信噪比为14 d B时的结果,信号长度为5 s。下面一组是信噪比为-4 dB时的计算结果,信号长度为10 s。由于信号谱线斜率为零,谐波搜索只需在θ=0的轴线上进行,而不必再进行ψ的搜索。基频搜索的结果为M=50,与时频图中谱线的位置一致,对应于基频频率M◦Δf=10 Hz。 图3 信噪比分别为14 dB和-4 dB时,谐波族信号的时频分布、Hough变换和基频搜索结果Fig.3 Time-frequency distribution,the Hough transformation,and base frequency result of the harmonic signal set while SNR=14 d Band SNR=-4 dB 图4 为一组频率时变的谐波族信号的时频分布及其Hough变换图。Hough变换网格数为200×300(θ范围为-π/4~π/4),信号频率变化率引起的时频面上基频谱线的斜率为-0.045,截距为8.67。根据Hough变换参数空间的极值点,计算得到相应的结果为-0.049和8.11,误差分别为8.9%和6.5%。 图4 频率时变谐波族信号的时频图及Hough变换Fig.4 Time-frequency distribution and Hough transformation of frequency-shifting harmonic signal set 在信噪比较高时,从图3第一组和图4的结果中,可以清楚看出信号时频面强度分布与Hough变换参数空间中分布的对应关系,通过搜索算法得到了信号基频的准确值(不可避免的,搜索过程中在基频的整数倍处也有幅度较低的峰值出现)。在图3的第二组结果中,即使信噪比降到-4 d B,在时频面上已很难分辨信号,但在谐波搜索曲线上,基频和其整数倍位置处仍有较其他位置高的幅度可供检测。 图4中计算误差主要有以下原因:1)由于时间-频率分辨率互相制约,即使信号频率为连续均匀变化,时频面上的谱线也不是细的连续直线,而是具有一定宽度的阶梯形状,这是误差的最主要来源,它与时频不确定原理相对应,难以大幅度消除;2)Hough变换过程中,Δt和Δf具有一定宽度,网格划分的疏密程度也有影响;3)多普勒效应引起的频偏不是严格的线性关系,在时频面的两端带来一定误差;4)k′n=tanθn≅θn的近似带来少量误差。图4中基频搜索结果与信号设定的参数基本无数值误差,只存在由于第1)和第2)项带来的小量不确定宽度。 基于时频面Hough变换的谐波检测算法有以下优点:1)符合无线通讯技术中可靠传输信息的频率分集模型,有效利用信号的多阶谐波分量;2)有效利用时频面上的时间积累效应;3)在信号频率随时间变化时,可以利用多阶信号的信息,求得频率变化率,精度比利用单阶信号时高;4)无论信号频率变化与否,在Hough变换参数空间的特征检测都较简单。 仿真结果表明,此法在低信噪比下仍有较好的检测性能,将会在螺旋桨驱动的直升机、无人机等军事目标的检测和识别领域中具有较好的应用前景。 [1]刘贯领.声目标识别方法研究[D].南京:南京理工大学,2003. [2]李在庭,高德勇.直升机声信号特征提取和识别技术[J].兵工学报,1996,17(1):55-59.LI Zaiting,GAO Deyong.Research on feature extraction and recognition technology of helicopter acoustic signal[J].Acta Armamentarii,1996,17(1):55-59. [3]吕国云,许学忠.战场目标被动噪声识别技术[J].探测与控制学报,2001,23(4):22-25.LV Guoyun,XU Xuezhong.Passive sound recognition technology for thetargetsin battlefield[J].Journal of Detection&Control,2001,23(4):22-25. [4]祝龙石,庄志洪,张清泰.战场声目标噪声特性分析[J].探测与控制学报(原现代引信),1996,18(2):57-61.ZHU Longshi,ZHUANG Zhihong,ZHANG Qingtai.Analyze on the character of the acoustic target in the war field[J].Journal of Detection&Control,1996,18(2):57-61. [5]唐玉志,刘瑜,郭艳,等.直升机谐波信号的多频循环平稳检测[J].探测与控制学报,2009,31(5):33-37.TANG Yuzhi,LIU Yu,GUO Yan,et al.Multi-frequency Cyclostationary Analysis of Harmonic Signal of Helicopter[J].Modern fuze,2009,31(5):33-37. [6]韩崇昭,朱洪艳,段战胜.多元信息融合[M].北京:清华大学出版社,2006. [7]廖明,谭晓衡,张志华.频率分集MC-CDMA在瑞利衰落信道下的性能分析[J].重庆邮电学院学报,2004,16(1):47-50.LIAO Ming,TAN Xiaoheng,ZHANG Zhihua.Performance of multi-carrier frequency diversity CDMA in Rayleigh fading channel[J].Journal of Chongqing University of Posts and Telecommunications,2004,16(1):47-50. [8]唐秋玲,覃团发,张淑仪.频率选择性衰落无线信道下的发送分集技术[J].南京大学学报(自然科学),2004,40(4):454-461.TANG Qiuling,QIN Tuanfa,ZHANG Shuyi.Transmit diversity scheme in the wireless channel of frequency-selective fading[J].Journal of Nanjing University(Natural Sciences),2004,40(4):454-461. [9]David E Newland.Harmonic wavelet analysis[J].Mathematical and Physical Sciences,1993,443:203-225. [10]李舜酩,许庆余.微弱振动信号的谐波小波频域提取[J].西安交通大学学报,2004,38(1):51-55.LI Shunming,XU Qingyu.Harmonic wavelet extraction for weak vibration signal in frequency domain[J].Journal of Xi'an Jiaotong University,2004,38(1):51-55. [11]唐玉志,董永峰.噪声和振动信号的谐波小波时频分布[J].噪声与振动控制,2009,29(4):42-45.TANG Yuzhi,DONG Yongfeng.Time-frequency distribution of acoustic and vibration signal based on the harmonic wavelet transformation[J].Noise and Vibration Control,2009,29(4):42-45. [12]冈萨雷斯.数字图像处理[M].北京:电子工业出版社,2003. [13]徐毓,杨瑞娟,李锋.Hough变换与数据融合[J].现代雷达,2001(6):16-18.XU Yu,YANG Ruijuan,LI Feng.Hough transform and data fusion[J].M odern Radar,2001(6):16-18.

1.2 二维图像的Hough变换[12-13]
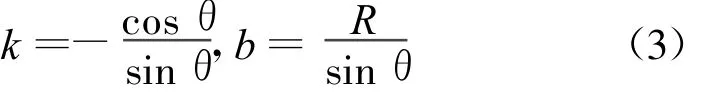

2 谐波族信号时频面的Hough变换
2.1 谐波信号频率平稳时的Hough变换
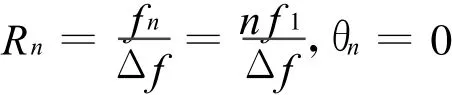
2.2 谐波族信号频率变化时的Hough变换



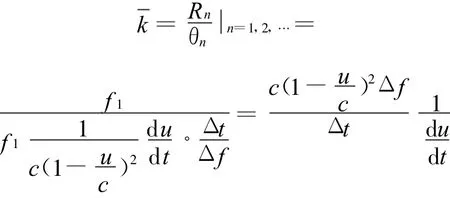

3 Hough变换参数空间中的谐波检测算法
3.1 ψ的搜索算法
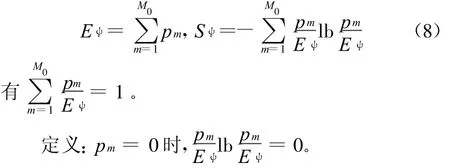
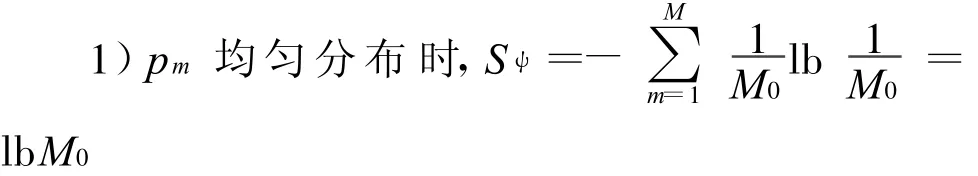

3.2 谐波基频搜索算法
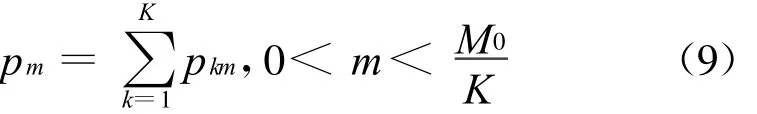
3.3 Pm的意义
3.4 算法的改进
3.5 Hongh变换网格与检测精度间的关系
4 仿真计算实例及分析
4.1 平稳谐波族信号的检测算例

4.2 频率时变的谐波族信号的检测算例
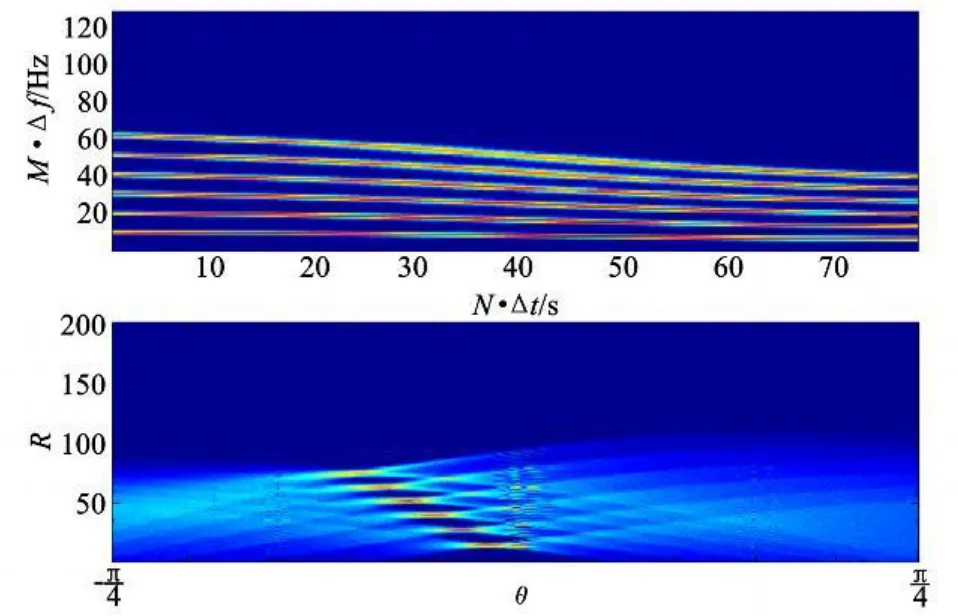
4.3 仿真结果分析
4.4 误差分析
5 结论
