基于参数优化的支持向量机战场多目标声识别

李京华,张聪颖,倪 宁

(西北工业大学电子信息学院,陕西西安 710072)

0 引言

战场目标声识别是被动声预警系统的核心内容之一。为了取得较好的识别结果并满足声预警系统的实际要求,建立的识别器必须高效、稳定、具有较好的推广价值[1]。在以往的研究中,人们多采用KNN分类器、神经网络分类器进行目标识别,并取得了一定的研究成果。但是,基于传统统计模式识别方法的KNN分类器依据样本无穷大下的渐近理论,即样本数趋于无穷大时其性能才有理论上的保证,而在战场目标识别中样本数通常是有限的,对于神经网络分类器存在有过学习和训练过程中的局部极小点问题。近年来,国际机器学习领域在不断发展统计学习理论的基础上形成了一种可用于模式识别的算法——支持向量机(Support Vector Machine,SVM)[2]。其在解决小样本、非线性及高维模式识别问题时表现出许多特有优势,且SVM得出的结果是有限样本信息下的最佳结论,得到的是全局最优点,从而解决了神经网络等学习方法的过学习、训练过程中的局部极小点问题。

作为一种新兴的机器学习方法,支持向量机也存在许多急需完善的地方。在支持向量机的构造过程中,支持向量机的参数(核函数参数σ与误差惩罚因子C)对最终分类精度有较大影响。合理的参数值可使支持向量机具有更高的精度、更好的泛化能力。针对常用的网格搜索[3]支持向量机参数的方法存在复杂度高、运算量大等不足,文中提出了一种改进的网格搜索SVM分类器的最佳参数选择算法。这种改进的网格搜索算法可以有效地减少运算量,在相对较短的时间内提高了识别率。

本文将小波能量谱作为战场目标声信号的特征向量,设计出一种基于改进的网格搜索SVM分类器用于目标识别。

1 战场目标声信号的特征提取

1.1 基于小波能量谱的特征提取算法

由多分辨分析[4]可知,同一尺度上的小波函数与尺度函数正交,根据小波变换的框架理论,当小波基函数是一组正交基函数时,变换具有能量守恒的性质,即满足:

式(1)表明将信号 f(t)小波分解后,其逼近近似信号系数与细节信号系数的平方和等于原始信号在时域上的能量。可见,信号的总能量等于各尺度重构信号能量之和。即小波变换将原始信号分解成不同频带的重构信号,每个重构信号的能量反应了原始信号在该频带内的能量。所以小波变换后的能量与原始信号的能量之间存在等价关系,按能量方式表示的小波分解结果称为小波能量谱。

对于战场上的目标来说,其被动声信号包含的能量分布与目标的大小、结构等特性密切相关,因此根据小波能量谱的定义,用小波能量谱来表示原始信号中的能量分布是可靠的,可以根据信号在不同频段上的能量分布特点,实现对不同类目标声信号的有效识别。

本文以实测直升机、战斗机、无人机、巡航导弹、坦克、汽车6类目标的声信号为研究对象,采样率均取为5 k Hz,采用db5小波对上述6类目标声信号分别进行10层小波分解,分解后取第10层低频系数的重构信号和各层高频系数的重构信号,其中s10为第10层低频系数的重构信号,s0～s9为第1层 ～第10层高频系数的重构信号。计算s0～s10的能量,归一化后,以各分解层的能量为元素,按照信号s10～s0的顺序将能量值排列形成特征矢量:T=[e10,e9,e8,…,e0]。各类目标各分解尺度上的归一化能量分布如图1所示。其中横坐标1上的能量表示尺度10上低频重构信号的能量,横坐标2～11表示尺度10～1的高频重构信号的能量。

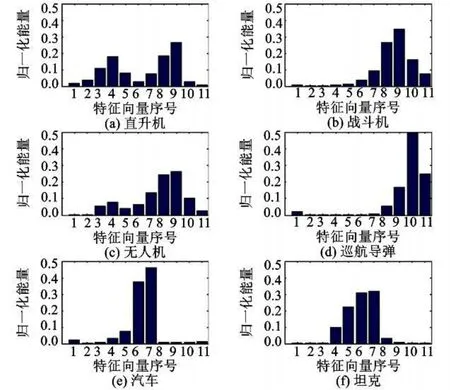
图1 各分解尺度上的归一化能量分布直方图Fig.1 Normalization Energy Histogram

1.2 模式特征向量的类别可分性评价

不同目标的差异性和相同目标的相似性,可以采用可分性测度来衡量。

在模式识别中,特征选择和特征提取的目的在于突出同一类别模式的相似性和不同类别模式之间的差异性,希望同一类模式在空间的分布越密越好,不同类的模式分布越分散越好。因此,类内距离和类间距离[5]可以作为可分性测度。

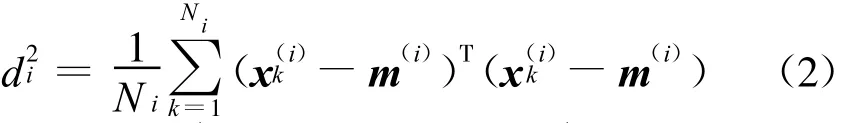
构造距离可分性测度计算公式为:

式中,dij为ωi和ωj类间平均样本距离,di为ωi的类内距离,d j为ωj的类内距离。该距离可分性测度反映了两类模式均值向量之间的距离与它们各类类内距离和的比值。

很显然,若类间平均样本距离d ij越大,各类类内距离之和越小,则可分性测度J越大,模式的可分性越好。若两类模式为同一类模式,则dij=di=dj,J=0.5。

利用公式(4)对小波能量谱法提取的目标特征向量作分析。将6类战场目标(直升机、战斗机、无人机、巡航导弹、坦克、汽车)的特征向量归一化后形成分析样本,每一类随机抽取30个样本,计算其可分性测度,重复进行100次取平均,计算结果列于表1中。

从表1中可以看出,基于小波能量谱法提取的特征进行识别时,巡航导弹和坦克最易区分识别,其次是直升机与坦克,而巡航导弹和汽车最不易识别区分。在后面的识别结果分析对比中将得到更进一步的验证。

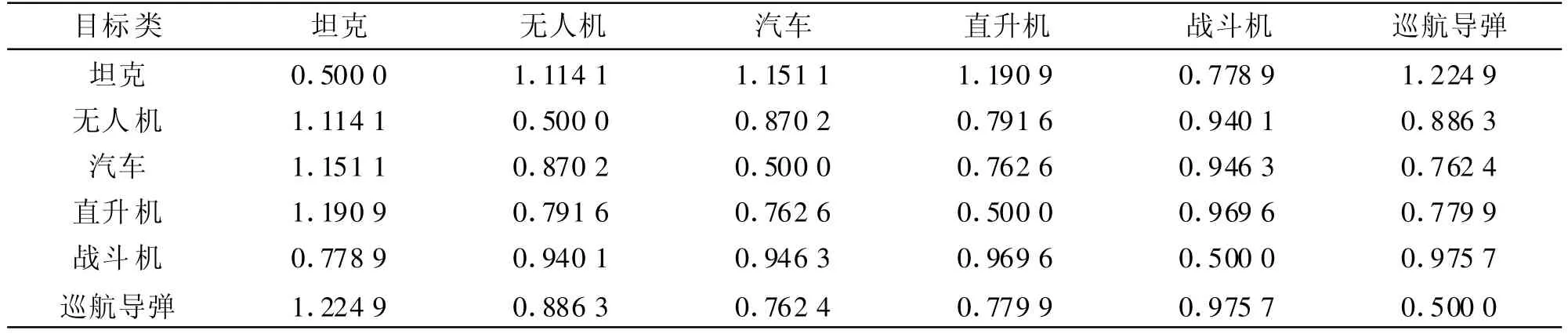
表1 战场目标特征向量的可分性测度Tab.1 Class separability measurement of battlefield targets feature vector

2 基于参数优化的SVM分类器

2.1 支持向量机基本原理

支持向量机主要解决的是一个二分类问题,该理论最初来源于数据分类问题的处理,SVM就是要寻找一个满足要求的分割平面,使训练集中的点距离该平面尽可能地远,即寻求一个分割平面使其两侧的margin尽可能大。支持向量机从线性可分情况下的最优分类面发展起来,通过将输入空间映射到一个高维内积空间中,解决一个线性约束的二次规划问题,得到全局最优解,保证收敛速度,不存在局部极小值问题[6-7]。

给定训练样本(x i,y i),i=1,2,…,N,集合{x i}∈Rn,y∈{-1,1}是类别标号,可以被一个超平面ω*x+b=0分开。使得每个样本都满足:

此时分类间隔为2/‖ω‖,因此使间隔最大等价于使 ‖ω‖2最小,满足式(5)且使 ‖ω‖2最小的分类面就是最优分类面。

利用Lagrange优化方法可以把上述最优分类面问题转化为其对偶问题,即求解如下的二次规划(QP)问题:

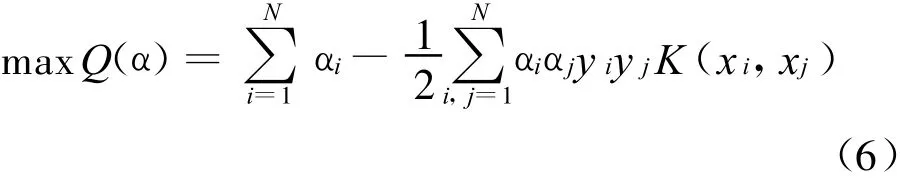
满足约束条件:

式中,K(xi,xj)为核函数;αi是二次规划问题所求的Lagrange乘子,每一个训练样本对应一个αi,根据Kuhn-Tucker条件知,只有一少部分αi不为零,所对应的样本就是支持向量;C为惩罚因子,它控制的是训练错误率与模型复杂度间的折中。

式中,b*是一个阈值。f(x)为SVM对于样本 x的输出,其值的正负表示其归属哪一类,由该式可看到那些αi=0的样本对分类没有任何作用,只有那些αi>0的样本对分类起作用。

针对战场多目标识别问题,需要的是多类分类器,本文采用1-a-1(One-against-one)算法,即每两类样本设计一个SVM分类器,这种算法简单,训练时间短。

2.2 核函数参数对SVM性能的影响

本文选用径向基函数(RBF)作为SVM分类器的核函数。对于一个基于RBF核函数的SVM,其性能是由参数(C,σ)决定的,选取不同的C和σ就会得到不同的SVM[8]。C的作用是控制对错分样本的惩罚程度,C的取值小表示对错分样本的惩罚程度小,分类面较简单。这时学习机器的经验误差相对较大。如果C无穷大,则所有的约束条件都必须满足,这就意味着所有训练样本都要准确地分类。这样,将导致分类面复杂,算法复杂度高,所需时间较长。因此对C值的选取要结合实际应用,在满足分类准确率的情况下取尽可能小的值来获得比较简单的判决函数。而核参数σ的改变实际上是隐含地改变映射函数从而改变样本数据子空间分布的复杂程度,即线性分类面的最大VC维[9-10],也就决定了线性分类达到最小误差。σ取值过小,所有的样本都将成为支持向量,故而造成对新样本的测试时间长,并且会产生“过度拟合”现象;当σ很大时,SVM的性能也会非常差,它对新样本的正确分类能力几乎为零,将把所有样本都判为同一类;当σ选取较好,支持向量的个数明显减少,并且此时分类器对新样本的正确判别能力有很大提高。

2.3 改进的网格搜索最佳参数选择算法

虽然用这种方法最终能找出最优化参数,但是其复杂度高,运算量大。

为了减少运算量,作为网格搜索法的一种改进,本文将最佳参数(C,σ)的选择分三步完成:

1)采用大的变步长,使最优参数的搜索在一个较大的范围内进行,实验中搜索范围取:

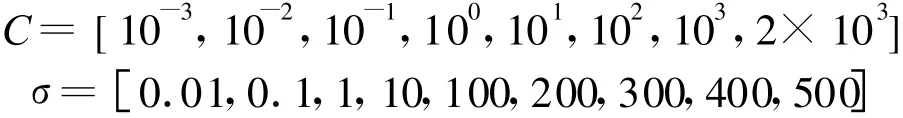
在这个大的粗搜索范围内得到识别率最高的C1opt、σ1opt值。

2)先固定C=C1opt,使σ在σ1opt附近采用较小的步长,在一个较小的范围内进行更细致的搜索,取:

选出识别率最高的σ2opt;

3)再固定σ=σ2opt,使C在C1opt的附近采用较小的步长,在一个小的范围内进行精细的搜索,取:

选出识别率最高的C2opt,至此(C2opt,σ2opt)即为所选的最优参数组合。

3 分类实验及结果分析

实验利用小波能量谱的特征提取方法对实测的6类战场目标:直升机、汽车、战斗机、无人机、坦克、巡航导弹的噪声信号提取特征向量,分别采用3种分类器:KNN分类器、改进的BP神经网络分类器和SVM分类器进行分类识别,得出分类结果,并根据实验结果分析比较3种分类器的分类性能。

本文所用的样本数据为:直升机220个样本,汽车325个样本,战斗机39个样本,无人机477个样本,坦克502个样本,巡航导弹40个样本。实验采用“交叉验证”(cross validation)的测试方法,这种方法能够充分利用样本提供的信息,弥补样本数量不足的缺陷,并可以防止过拟合的问题。将所有特征向量样本均匀分成3组(F1,F 2,F3),样本划分情况如表2所示。

表2 交叉验证测试样本划分情况Tab.2 Division method of the cross validation samples

并按以下步骤做3次测试:

第一次测试:训练集:F 1+F2,测试集:F 3;

第二次测试:训练集:F1+F 3,测试集:F2;

第三次测试:训练集:F2+F 3,测试集:F1。

每次测试的正确识别率按下面公式计算:

3种分类器的识别结果如表3所示。

表3 不同分类器的目标识别率Tab.3 Classification accuracy of different classifiers

由分析表3的分类结果可知,基于小波能量谱法提取的特征是有效的,3种不同的分类器总的识别率都达到了84%以上。在本实验中,改进BP神经网络分类器的识别效果好于KNN分类器,SVM分类器的效果最好。进一步说明了文中提出的改进的网格搜索SVM分类器最佳参数选择算法可以有效地减少SVM分类器的运算量,改进学习性能并提高识别率。

4 结论

本文以实测战场目标辐射噪声信号为研究对象,采用小波能量谱特征提取方法提取各类目标的特征向量,设计了一种改进的网格搜索SVM分类器,对比实验结果表明改进后的SVM分类器从实用性和分类效果上都好于KNN分类器和改进的BP网络分类器,良好的实验结果说明了改进的网格搜索优选SVM参数算法的有效性。在实际应用中,需要足够量的模式样本来提取目标类的特征,若样本数量太少,将使分类器的性能降低,并最终影响识别率,如本实验中战斗机和巡航导弹的样本量较少,识别率比其他类别目标就低一些。

[1]陈虎虎,钟方平.基于支持向量机的低空飞行目标声识别[J].系统工程与电子技术,2005,27(1):46-48.CHEN Huhu,ZHONG Fangping.Acoustic recognition of low-altitude flight targets by SVM[J].Systems Engineering and Electronics,2005,27(1):46-48.

[2]Vapnik V N.The nature of statistical learning theory[M].New York:Springer Verlag,1995.

[3]Chapelle O,Vapnik V.Choosing multiple parameters for support vector machines[J].Machine learning,2002,46(1/2/3):131-159.

[4]Mallat S.A theory for multiresolution signal decomposition:the wavelet representation[J].IEEE Transaction on Pattern Analysis and Machine Intelligence,1989,11(7):674-693.

[5]孙继祥.现代模式识别[M].长沙:国防科技大学出版社,2002.

[6]Buges,C J C.A tutorial on support vector machines for pattern recognition[J].Data mining and knowledge discovery,1998,2(2):121-167.

[7]邓乃扬,田英杰.数据挖掘中的新方法:支持向量机[M].北京:科学出版社,2004.

[8]林升梁,刘志.基于RBF核函数的支持向量机参数选择[J].浙江工业大学学报,2007,35(2):163-167.LIN Shengliang,LIU Zhi.Parameter selection in SVM with RBF kernel function[J].Journal of Zhejiang University of Technology,2007,35(2):163-167.

[9]WU Kuoping,WANG Shengde.Choosing the kernel parameters for support vector machines by the inter-cluster distance in the feature space[J].Pattern Recognition,2009,42(5):710-717.

[10]王睿.关于支持向量机参数选择方法分析[J].重庆师范大学学报(自然科学版),2007,24(2):36-38.WANG Rui.Method analyse about support vector machins parameter[J].Journal of Chongqing Normal U-niversity,2007,24(2):36-38.