基于辅助模型的改进粒子滤波算法
2010-08-27李亚安李国辉
何 健,李亚安,易 锋,李国辉,2
(1.西北工业大学航海学院,陕西西安 710072;2.西安邮电学院电信系,陕西西安 710061)
0 引言
非线性系统的估计问题广泛存在于许多领域,包括统计信号处理、经济学、雷达跟踪、飞行器导航、声纳等,其中最主要的问题就是对非线性状态的后验概率密度函数(PDF)进行估计,但在实际中很难直接对PDF进行表示,在非线性高斯条件下,传统的解决方法是利用 EKF(Extended Kalman Filter)[1]和 UKF(Unscented Kalman Filter)[2],其中EKF是结合卡尔曼滤波算法对非线性部分进行线性化处理的一种次优估计算法。而 UKF避免了EKF线性化等近似方法,无需计算Jacobian矩阵,提高了估计精度。Rudolph Vander Merwe和 Eric A.Wan在 UKF的基础上给出了SRUKF(Square Root Unscented Kalman Filter)[3]算法。UKF每次更新中都要对Sigma点花费大量的计算,并要求计算状态协方差矩阵的平方根;在SRUKF中,平方根被直接记录下来,避免了每次采样时的重新因数分解,并且得到的协方差阵一定是非负的,因而确保了算法的稳定性。近几年发展起来的粒子滤波PF(Particle Filter)[4]是一种基于蒙特卡罗的贝叶斯状态估计算法,它通过一组归一化权值的粒子来近似表示PDF,适用于非线性、非高斯条件下的目标跟踪。在粒子滤波器中,普遍存在的问题是粒子退化现象,即经过几次迭代,除一个粒子外,其他粒子都减少到可以忽略的程度。降低该现象影响的最有效方法是选择建议分布函数和重采样方法。UPF(Unscented Particle Filter)[5]采用 UKF来计算建议分布,粒子的产生充分利用了新的测量信息,可以使其建议分布较好地逼近后验概率密度,如果测量噪声过大,UKF很容易产生目标失捕问题[6]。SPPF(Sigma Point Particle Filter)[7]则是利用SRUKF来计算建议分布,可以使建议分布更好地逼近后验概率密度。
针对SPPF算法在非线性、非高斯系统的目标跟踪精确度不太高这一问题,本文提出了一种改进Sigma粒子滤波算法MSPPF(Modified Sigma Point Particle Filter)。
1 SPPF滤波算法
1.1 贝叶斯估计原理
假定动态时变系统可描述为
系统方程:

量测方程:
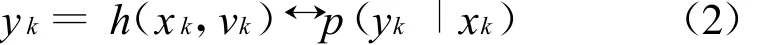
式中,f和h为系统状态和量测的非线性变换,xk,yk分别是系统k时刻的状态值和量测值,wk,v k分别是系统k时刻的状态噪声和测量噪声。则状态预测方程和状态更新方程分别为:

1.2 粒子滤波算法
PF是通过蒙特卡罗方法实现贝叶斯递归估计。从待估计的后验分布p(x0:k|y0:k)中抽样出N个独立同分布的粒子和相应的归一化权值(x0:k),则分布p(x0:k|y 0:k)的一个估计表示为:
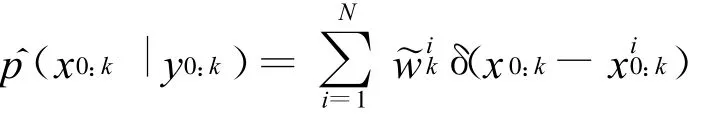
当无法从后验分布p(x0:k|y0:k)中直接采样时,可以找一个容易采样的密度分布函数q(x0:k|y0:k)(建议分布)中采样。
令其中w(x 0:k)为重要性权值:
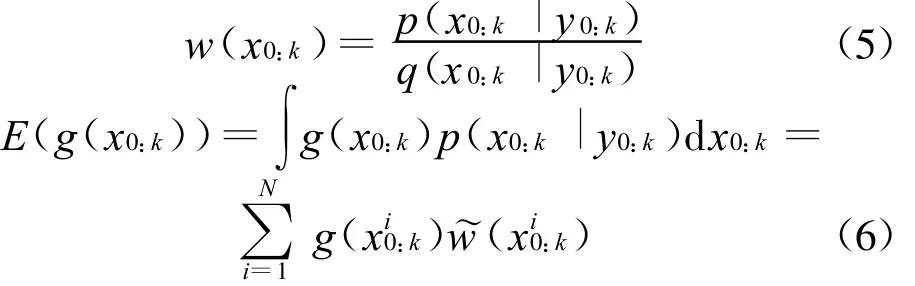
PF的实现步骤:
1)初始化k=0
从p(x0)采样粒子{xi0:k,i=1,…,N}
2)重要性权值的计算
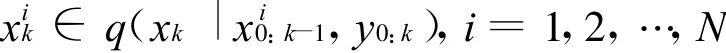
粒子权值更新方程:
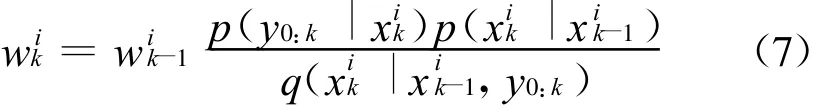
4)重采样
从xik中根据重要性权值重新采样得到新的N个粒子~xik,并重新分配权值 ~wik=1/N。

随着迭代次数的增加,重要性权值的分布变得越来越倾斜,有可能出现粒子匮乏现象,为了避免粒子匮乏,Goden[8]等提出了重采样方法,主要思想就是去掉那些权值小的粒子,复制权值大的粒子。
1.3 SPPF算法
在粒子滤波器中,关键问题就是对建议分布的选择。当q(x k|:k-1,y0:k)=p(xk|:k-1,y 0:k)时,重要性权值条件方差最小,为最优重要性函数,实际上,很难对它进行采样。在应用中更常使用先验概率密度来作为建议分布:

由于函数没有新的测量信息,它的性能主要依靠观测噪声的方差,当观测噪声的方差很小时,它的性能就很差。而SPPF是利用SRUKF来更新粒子均值和方差,从而用高斯近似的方法作为建议分布密度函数∈q(xk|-1,y0:k)=,),其中 N(◦)表示高斯函数。
2 基于SRUKF和辅助模型的改进Sigma粒子滤波算法
先称(1)、(2)为主模型,这里主要介绍一种辅助模型并使用SRUKF和它共同来产生建议分布。
2.1 辅助模型
定义辅助模型[9]为:
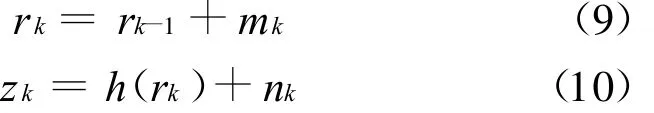
这里mk是一个小方差高斯噪声,观测噪声nk和(2)中的vk认为是一样的。如果h(◦)是线性的,nk是高斯噪声,卡尔曼滤波就可以对rk进行最优估计。在实际环境中,h(◦)往往是非线性的,就可以使用SRUKF来对r k进行估计。
2.2 改进Sigma粒子滤波算法(MSPPF)
在时刻k,从由SRUKF产生的建议分布密度中采样第一个粒子,然后把和辅助模型结合并使用SRUKF产生新的建议分布,从中采样第二个粒子。重复这个过程,递归的获得,…,N表示的粒子的总数。当观测噪声很小时,除了第一个粒子是从主模型中获得外,其他的粒子都是从第一个粒子和辅助模型递归得到的,这N-1个粒子充分利用了新信息yk,因此MSPPF能更好地近似后验概率密度。
MSPPF的算法步骤:
2)重要性采样:
3)重要性权值:
当i=2,…,N时,
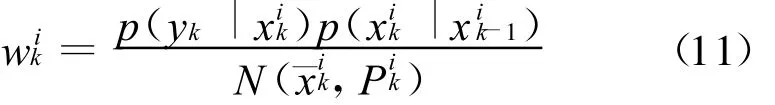
4)重采样:
3 仿真结果与分析
为了证明MSPPF的性能,考虑一个非线性非高斯模型[1,5]。
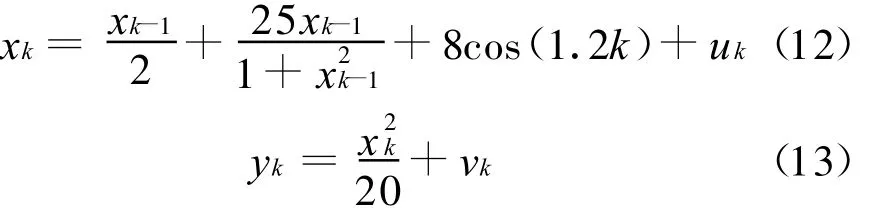
这里w=4e-2,uk服从Gamma(3,2)分布,观测噪声v k服从高斯分布N(0,10-5),目标的初始状态x0=1,经过100次蒙特卡罗仿真,每次仿真时间是60 s,采样间隔为1 s。1次独立试验的均方根误差定义为:
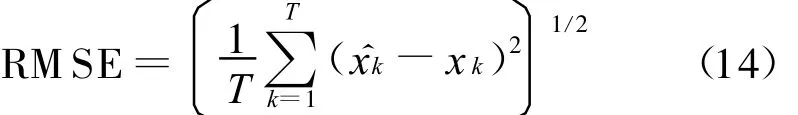
其中 PF、UPF、SPPF、MSSPF的粒子数分别为1 000,200,200,20。图1、图2表示各个滤波算法对目标状态的估计曲线和均方根误差曲线图。
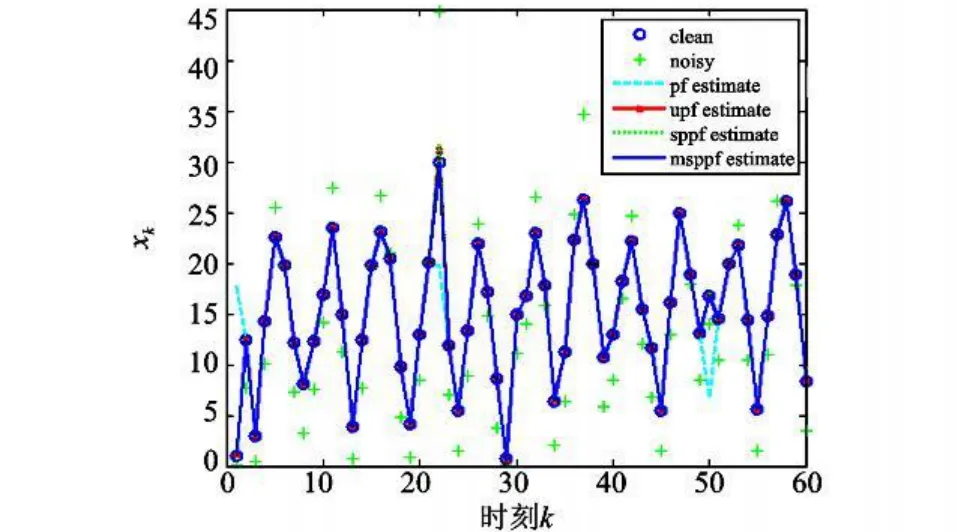
图1 不同滤波器的状态估计Fig.1 State estimation for different filters

图2 100次蒙特卡罗仿真的RMSEFig.2 RMSE for 100 times Monte-Carlo simulations
从上图可以看出,在非高斯环境中,由于PF中没有包含最新的测量信息,所以它受噪声的干扰比较大,算法不稳定,跟踪性能不好。UPF和SPPF各自生成的建议分布中有效地利用了测量信息,在粒子数比较少的情况下,具有较高的精确度。而本文提出的MSSPF由辅助模型和SRUKF共同来产生建议分布,它比其他的算法更能有效地利用测量信息,所以只需要20个粒子就可以达到很高的精度。
表1给出了重复进行100次蒙特卡罗实验得到的 MSPPF 与 EKF、UKF、PF 、UPF、SPPF 性能对比统计结果。可以看出它们对状态估计的均方根误差(RMSE)均值和方差的变化。
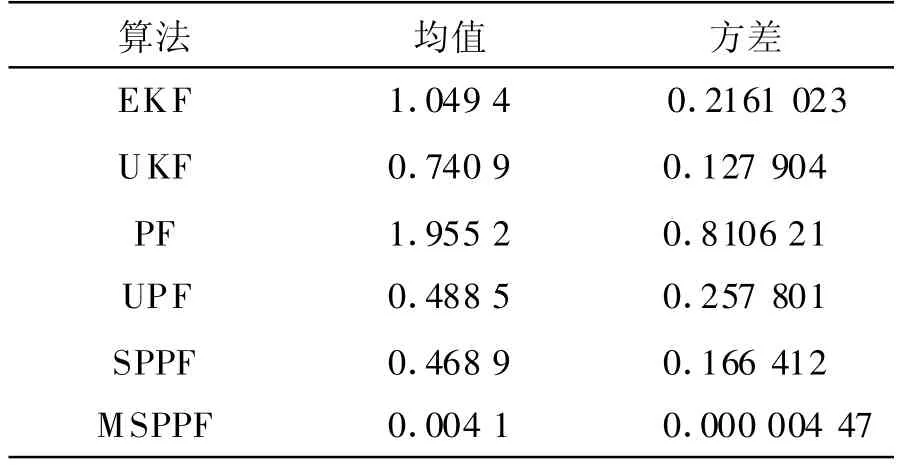
表1 RMSE的均值和方差Tab.1 The mean and variance of RMSE
4 结论
对于非线性非高斯问题,粒子滤波在迭代过程中经常会出现粒子退化现象,本文提出了一种改进Sigma粒子滤波算法MSPPF。该算法采用了辅助模型与SRUKF来构造建议分布,有效地利用了新的测量信息,使建议分布能更好地逼近后验概率密度。仿真结果表明,MSPPF不仅具有很好的稳定性,而且用很少的粒子就可以达到很高的跟踪精度。MSSPF是一种效率高、性能好的跟踪算法。
[1]Gordon N J,Salmond D J,Smith A F M.Novel approach to nonlinear/non-Gaussian Bayesian state estimation[J].IEE F Proceedings Radar and Signal Processing,1993,140(2):107-113.
[2]Julier SJ,Uhlmann JK.Unscented filtering and nonlinear estimation[J].Proceeding of the IEEE,2004,92(3):401-422.
[3]Merwe R V,Wan E A.The Squre-root Unscented Kalman Filter for State and Parametere-estimation[J].International Conferenceon Acoustics,and Speech signal Processing,2001:3 461-3 464.
[4]Arulampalam S,Maskell S,Gordon N.A tutorial on particle filters for online nonlinear/non-Gaussian bayesian tracking[J].IEEE Trans Signal Processing,2002,50(2):174-188.
[5]Van der Merwe R,Doucet A,Nando de Freitas,et al.The Unscented Particle Filter[R].GB:Cambridge University Engineering Department,2000.
[6]肖延国,余志军,魏建明.一种改进的无迹粒子滤波器在目标跟踪中的应用[J].中国科学技术大学学报,2008,38(2):183-188.XIAO Yanguo,YU Zhijun,WEI Jianming.An improved unscented particle filter for target tracking in sensor networks[J].Journal of University of Science and Technology of China,2008,38(2):183-188.
[7]Guo Wen Y,Han CZ,Lei M.Improved Unscented Particle Filter for Nonlinear Bayesian Estimation[J].Information Fusion,2007(10):1-6.
[8]Doucet A,Godsill S,Andrieu C.On sequential Monte Carlo methods for Bayesian filtering[J].Statistics and Computing,2000,10(3):197-208.
[9]Chen Qi,Bondon P.A new unscented particle filter[J].International Conference on Acoustics,Speech and Signal Processing,2008:3 417-3 420.
