S型MEMS平面微弹簧垂直弹性系数
2010-08-27李晓杰牛兰杰
李晓杰,牛兰杰,翟 蓉,殷 群
(1.机电工程与控制国家级重点实验室,陕西西安 710065;2.西安机电信息研究所,陕西西安 710065)
0 引言
随着微机电系统(MEMS)技术的不断成熟和发展,MEMS器件在引信中的应用越来越受到重视。与传统引信相比较,MEMS引信具有体积小、成本低、能耗低和可靠性高等特点。弹簧是引信中最常用的力学机构之一,如后坐簧、离心簧等,在MEMS引信中也不例外[1-2]。但是MEMS引信中的微弹簧结构外形、尺寸以及加工方法均与传统弹簧存在着很大的差异,大多没有成熟的设计公式,目前主要是利用有限元仿真获得弹性系数。微弹簧的设计和优化存在着诸多不便。
Lishchynska M.[3]和Fukushige T.[4]等分别研究了直梁型微弹簧和锥型弹簧结构形状参数对静电力作用下器件性能的影响。何光、石庚辰和李华[5-10]推导了“Z 型”、“S型”、“W 型”和“L型”MEMS平面弹簧水平弹性系数计算公式,并通过有限元仿真和试验验证了其正确性,但由于弹簧应力集中以及弯角处等效纯弯矩的影响[11],公式精度还有待进一步提高。在此基础上,南京理工大学的吴志亮、常娟[11]利用ANSYS仿真对公式进行了优化,优化后弹性系数计算公式平均误差低于1%,准确度较高。但前期研究多仅限于弹簧水平方向弹性系数,平面弹簧传统应用只考虑水平弹性系数,难以确切描述弹簧的形变特性,本文提出“S型”平面微弹簧垂直方向弹性系数计算公式。
1 卡氏第二定律和胡克定律
“S型”平面微弹簧由n节结构相同的基本单元组成,且结构对称。其结构形式及结构参数如图1所示。图中L为微弹簧直梁长度,H为微弹簧横截面厚度,B为微弹簧横截面宽度,R为弯半径。

图1 “S型”平面微弹簧结构形式及参数Fig.1 The structure parameters of the microsprings
在微弹簧的线弹性范围内,求解弹簧弹性系数按以下两个步骤进行:
1)运用能量法——卡氏第二定律[12]求解力作用点方向的线性位移,其表达式为:
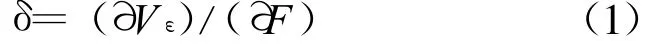
式中,δ为结构在力作用方向上的位移,F为作用力,Vε为在力F作用下弹簧的应变能。
2)根据胡克定律,弹性系数k则可以表示为:

2 垂直方向弹性系数公式
当力垂直作用于弹簧一端时,力引起的轴向变形很小,可以忽略,只需考虑弹簧截面受到弯矩以及扭矩的作用。弹簧的总应变能表示为:
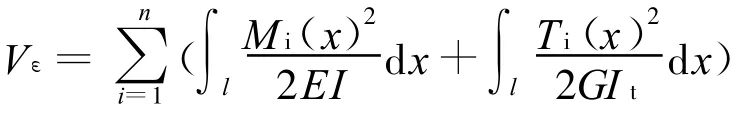
式中,I=BH3/12,G=2E/(1+ε),I t=βHB3;M i(x)为弹簧截面所受的弯矩;E为材料的弹性模量;I为截面的惯性矩;T i(x)为弹簧截面所受的扭矩;G为材料的切变模量;ε为弹簧材料的泊松比;I t为极惯性矩;β是与H/B比值相关的系数,可查表得到[12]。
取第一节弹簧进行分析,如图2所示,将其分成①②③④⑤5个部分,假定其一端固定,一端受到垂直纸面的力F。

图2 单节弹簧垂直方向受力示意图Fig.2 The force diagram of a unit microspring
分段应用卡氏第二定律进行分析,第①段:

所以第①段的位移为:
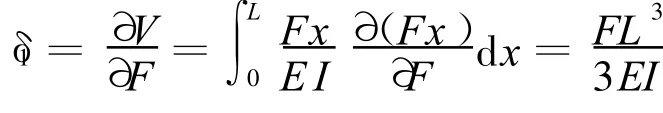
第②段:
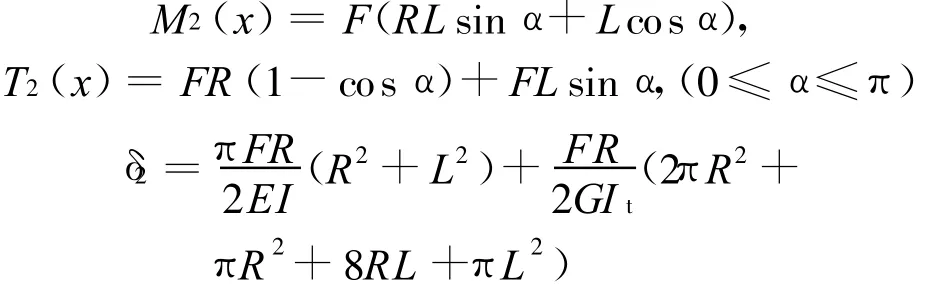
第③段:
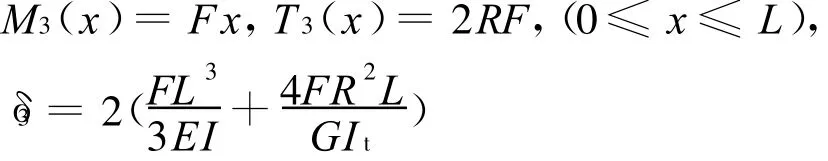
第④段和第②段求解类似,
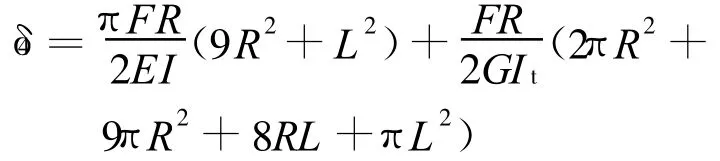
第一节弹簧的位移δp1=δ1+δ2+δ3+δ4+δ5,同样方法计算剩余n-1节弹簧的变形位移,n节弹簧位移叠加即为弹簧总位移δ总。故n节的弹簧垂直弹性系数kvertical为:

3 有限元仿真验证
为了验证公式推导的正确性,利用有限元仿真软件ANSYS10.0对该微弹簧进行结构仿真。选取弹簧的结构参数为:L=500μm,H=200 μm,B=80μm,R=100 μm,n=7。弹簧材料为镍(Ni),其弹性模量(EX)E=1.80×105MPa,泊松比(PRXY)ε=0.3。
按照上述参数在 ANSYS中建立模型,按μMKS单位制输入,单元结构选SOLID95,网格划分长度定义为“20”,分析类型为静态分析(Static)。弹簧一端施加全约束(ALL DOF)边界条件,另一端垂直方向施加500μN的力,仿真结果如图3所示,虚线位置为弹簧的初始状态。
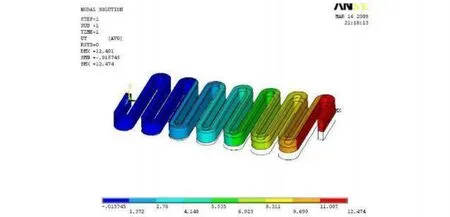
图3 微弹簧垂直力作用下的仿真结果Fig.3 Simulation results of ANSYS
由图3可以看出在500μN力的作用下,弹簧垂直方向的伸长量为12.474μm。在弹簧的线弹性范围内,根据胡克定律,得弹性系数为40.1 N/m。将弹簧结构参数代入公式(3),则计算得弹簧垂直弹性系数理论值为39.5 N/m。比较仿真值与理论值,见表1,其相对误差小于2%,两者基本吻合,验证了公式(3)的正确性,对比结果见表1.
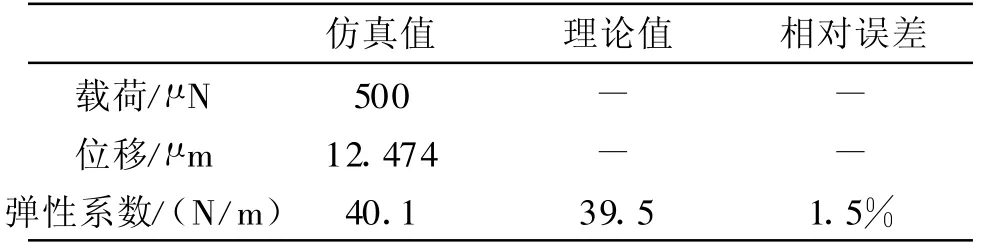
表1 仿真模拟与理论计算对比Tab.1 Constants contrasting different methods
4 结构参数对垂直弹性系数的影响
分别改变弹簧节数、弯半径、直梁长度、梁宽和梁厚,保持其它结构参数不变,用ANSYS10.0对弹簧进行有限元仿真,得到5组不同结构参数下弹簧垂直方向弹性系数的变化特性。同时,利用公式(4)计算5组结构参数下弹簧弹性系数,并将两者进行比较。最后,分别直线拟合仿真和理论数据点,结果如图5所示。
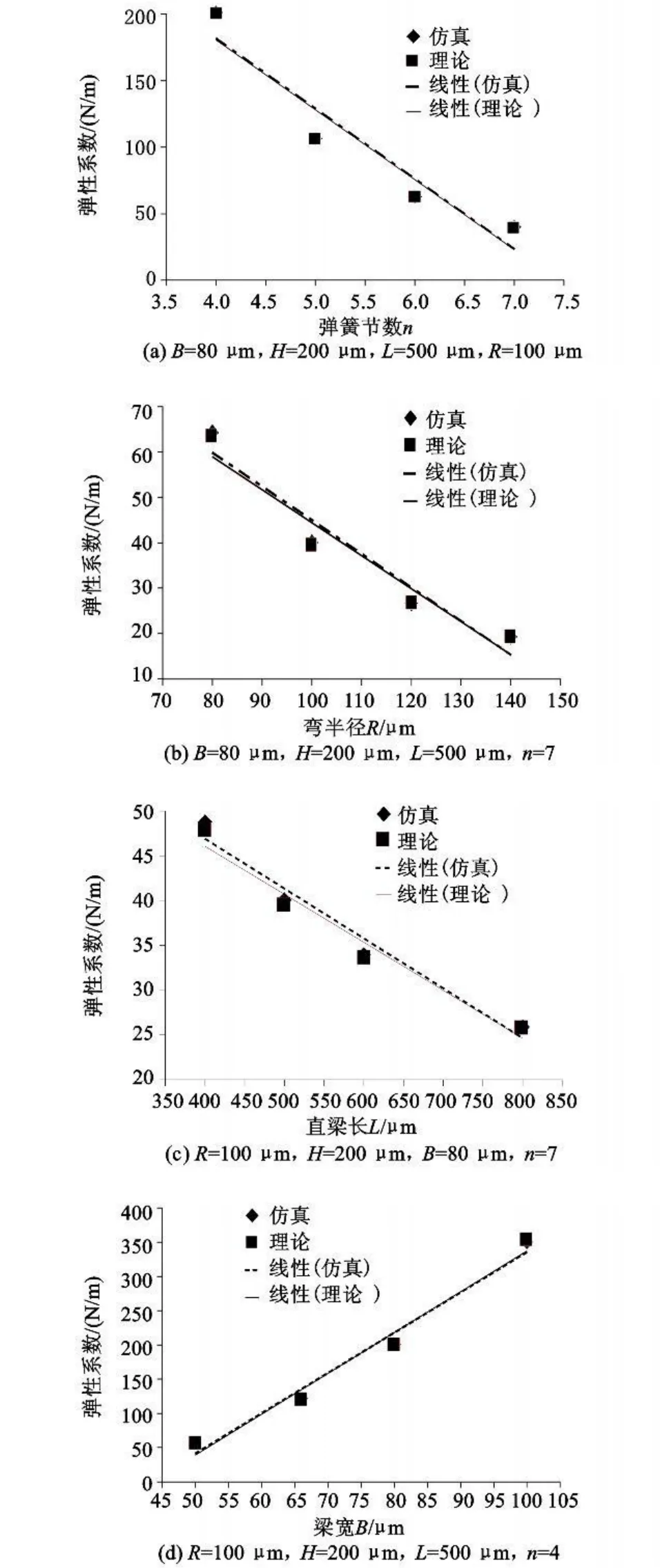

图4 弹簧垂直弹性系数随结构参数的变化关系Fig.4 Dependence of microspring constant on its configurations
从图4中可以看出,在其它结构参数一定的情况下,弹簧垂直方向弹性系数随节数n、弯半径R以及直梁长度L的增大而减小,随梁的宽度B和厚度H的增大而增大。其中弹簧节数n和梁宽B的变化对弹簧垂直弹性系数的影响最为明显,因为图 5(a)、(b)中直线的斜率绝对值最大。因此在设计过程中,如果要大幅调整弹性系数,可以先考虑改变节数n或宽度B,其它参数可用作微调。
图4中ANSYS仿真和公式计算得到的垂直方向弹性系数相对误差较小,直线拟合也极为接近,可见用仿真和理论结果比较吻合,进一步表明上述推导的垂直方向弹性系数计算公式是正确的。
5 结论
本文运用卡氏第二定律和胡克定律,推导出“S型”平面微弹簧垂直方向弹性系数计算公式,ANSYS有限元仿真表明,其相对误差小于2%,并且弹簧垂直方向弹性系数随节数n、弯半径R以及直梁长度L的增大而减小,随梁的宽度B和厚度H的增大而增大,为“S型”平面微弹簧的设计和优化提供理论依据,但对于微弹簧的动力学响应还有待进一步分析。
[1]冯鹏洲,朱继南,吴志亮.美国典型 MEMS引信安全保险装置分析[J].探测与控制学报,2007,29(5):26-30.FENG Pengzhou,ZHU Jinan,WU Zhiliang.Analysis of US typical MEMS fuze safety&arming device[J].Journal of Detection&Control,2007,29(5):26-30.
[2]Charles H Robinson,Silver Spring.Omnidirectional Microscale impact switch[P].US,6765160,2004.
[3]Lishchynska M,O'Mahoy C,Slatery O,et al.Comprehensive spring constant modeling of tethered micromechanical plates[J].Journal of Micromechanics and Micro-engineering,2006,16(6):S61-S67.
[4]Fukushige T,Hata S,Shimokohbe A.A MEMS corrical actuator array[J].Journal of Micro-engineering system,2005,14(2):243-253.
[5]何光,石庚辰.基于MEMS技术的平面 W型微弹簧刚度特性研究[J].北京理工大学学报,2006,26(6):471-474.HE Guang,SHI Gengchen.Study on stiffness characterization of planar W-form micro-springs based on MEMS technology[J].Transactions of Beijing Institute of Technology,2006,26(6):471-474.
[6]何光,石庚辰.平面S型与平面W型MEMS弹簧性能比较研究[J].传感技术学报,2008,21(2):288-291.HE Guang,SHI Gengchen.Comparative study on stiffness characterization of planar S&W-form micro-springs based on MEM S[J].Chinese Journal of Sensors and Actuators,2008,21(2):288-291.
[7]李华,石庚辰.MEMS平面微弹簧刚度分析[J].压电与声光,2007,29(2):237-239.LI Hua,SHI Gengchen.The stiffness analysis of MEMS planar microspring[J].Piezoelectrics&Acoustooptics,2007,29(2):237-239.
[8]李华,石庚辰.MEMS平面微弹簧弹性系数的研究[J].探测与控制学报,2005,27(4):41-43.LI Hua,SHI Gengchen.Study on the elastic coefficient of MEM S planar microspring[J].Journal of Detection&Control,2005,27(4):41-43.
[9]李华,石庚辰.MEMS微弹簧应用模式分析[J].传感技术学报,2007,20(12):2 709-2 712.LI Hua,SHI Gengchen.Analysis of application pattern of MEM S microspring[J].Chinese Journal of Sensors and Actuators,2007,20(12):2 709-2 712.
[10]杨卓青,丁桂甫.用于MEMS惯性开关的微弹簧有限元动力学分析[J].机械强度,2008,30(4):586-589.YANG Zhuoqing,DING Guifu.Finite element dynamics analysis of microspring in MEMS inertial switch[J].Journal of Me-chanical Strength,2008,30(4):586-589.
[11]吴志亮,常娟,冯鹏洲,等.引信用 MEMS平面微弹簧弹性系数分析[J].南京理工大学学报,2008,32(2):140-144.WU Zhiliang,CHANG Juan,FENG Pengzhou,et al.Elastic coefficient analysis of MEMSplanar microspring used in Fuse[J].Journal of Nanjing University of Science and Technology(Natural Science),2008,32(2):140-144.
[12]刘鸿文.材料力学[M].北京:高等教育出版社,2004.
