定数截尾情形下一类分布族参数的Minimax估计

任海平，李中恢

（1.江西理工大学 基础部，南昌 330013；2.江西宜春学院 数学与计算机科学学院，江西 宜春 336000）

0 引言

分布族参数的Minimax估计问题，一直引起很多学者的兴趣，见文[1-6]。在加权平方损失函数和MLINEX损失函数下，文[1]、[2]研究了Parteo分布参数的Minimax估计和风险函数问题，文[3]讨论了Rayleigh分布参数Minimax估计问题；文[4]在对数误差平方损失函数和MLINEX损失函数下，讨论了一类转换的χ2分布族参数的Minimax估计问题；文[5]在LINEX损失函数下研究了成功概率的Minimax估计问题；文[6]通过参数变换得到了一类分布函数参数的Minimax估计.大多数Bayes推断程序已经在通常的平方损失函数下得到了发展，平方误差损失是对称的，它予于了高估和低估具有同等的重要性。然而这样的一个限制可能是不合实际的。例如，在估计可靠性及失效率函数时，高估会比低估带来的后果更严重，在这种情况下使用对称损失函数可能是不合实际的[7].于是很多学者提出了一些非对称损失函数。

Podder[1]提出了一个修正的线性指数损失函数(MLINEX损失函数)：

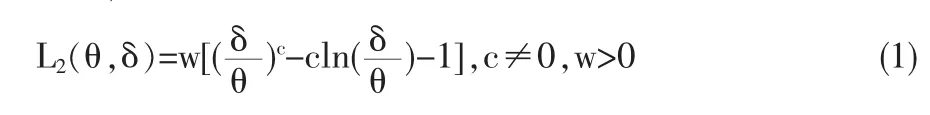
本文考虑如下一类分布族:

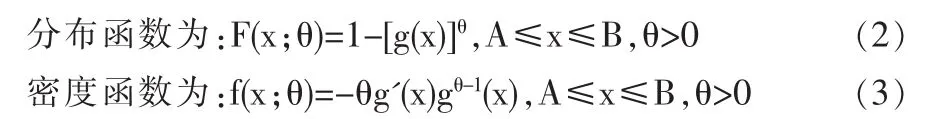
其中g(x)是关于单调递减的可微函数，且g(A)=1，g(B)=0,其中θ为未知参数，很多重要的分布都属于这一类分布族。

在生存分析、可靠性和保险精算问题中有各种各样与寿命或失效时间有关的试验数据，称为寿命数据.完全寿命试验要进行到所有试验样本寿命结束为止，统计分析的结果虽较可靠，但常常需要较长时间，特别是随着科学技术的进步，产品的质量也不断提高，产品的寿命越来越长，所以在这些情形下完全寿命试验难于采用，此时我们只能获得部分数据，但若能充分利用寿命分布提供的信息，也能得到较有效的统计分析结果，且省时、经济、具有实用价值.定数截尾寿命试验又称为Ⅱ型截尾寿命试验,就是其中一种较常采用的截尾试验。

本文将基于定数截尾试验，在加权平方误差损失函数和MLINEX损失函数下，讨论了此类分布族参数Minimax估计问题。

1 引理及证明

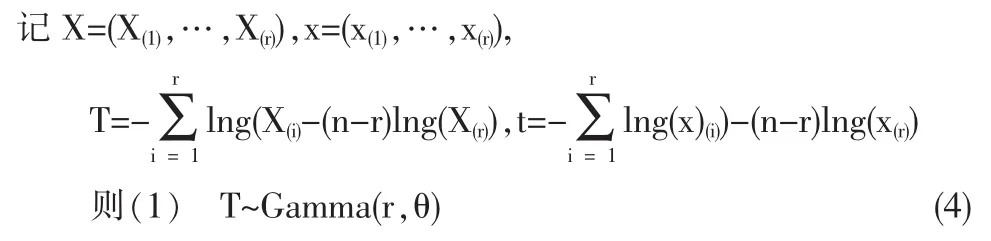
引理1 设X1，…，Xn为来自分布族(3)的一个简单随机样本，在定数截尾试验中,进行到有r个产品(r事先指定,r＜n)失效时试验终止, 获得 r个观察值 x(1)＜x(2)＜…＜x(r).

（2）假定参数θ具有Jeffery's无信息先验密度：π（θ）∝

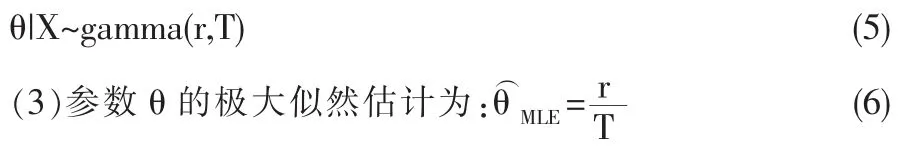
证明：在定数截尾（Ⅱ型截尾）下，样本的似然函数为：

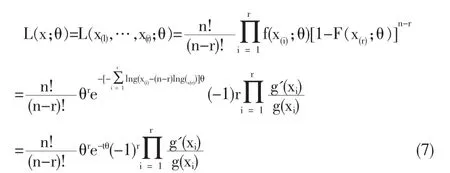
其中A≤x(i)≤B

则u(x)的矩母函数Φ(w)为：

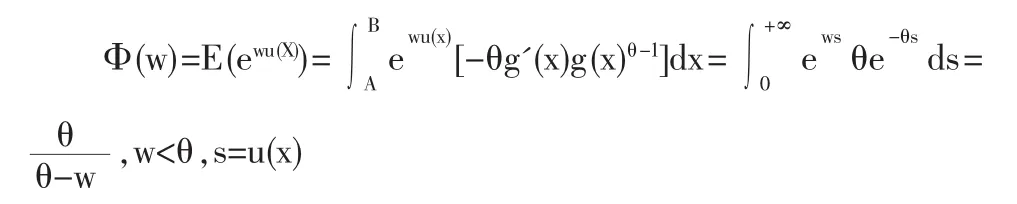
于是 u(X)～Gamma(1，θ)

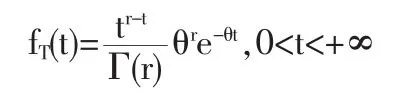
（1)设参数 θ 具有 Jeffery’s无信息先验密度：π （θ）∝的联合密度函数为：

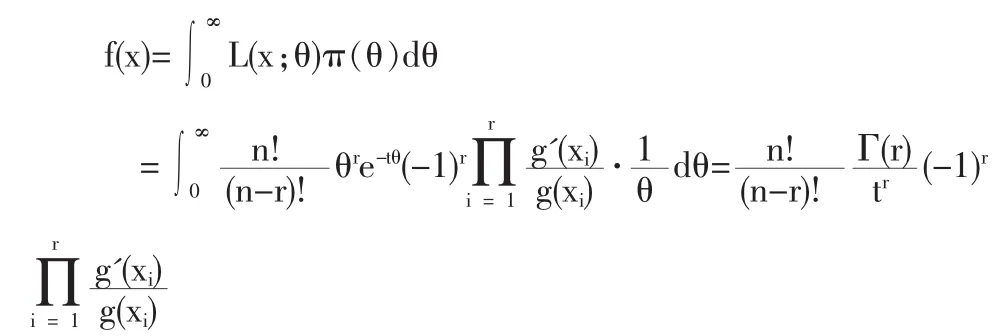
给定样本X=(X1，…，Xn)后参数θr的后验概率密度为：

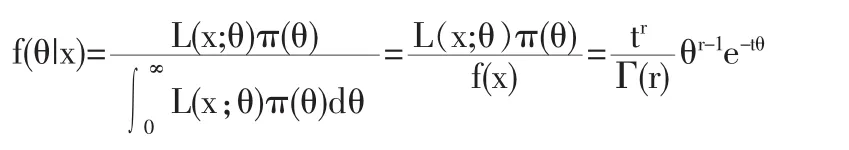
于是 θ｜X～Gamma(r,T).

引理 2[10]在加权平方损失函数为：

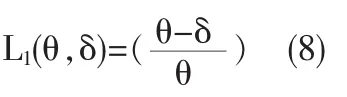
下，其中δ为θ的判别空间的一个估计，则对于任意的先验分布 π（θ），θ 的 Bayes 估计为并且解是唯一的，这里假定 r(δ)=E(θ，δ)[L2（θ，δ）]＜+∞

引理3 在MLIEX损失函数L2(θ，δ)=w

证明：在MLIEX损失函数下，δ对应的Bayes风险为：

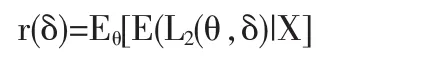
故欲使 r(δ)达到最小，只需 E(L2(θ，δ)｜X)几乎处处达到最小。

由于

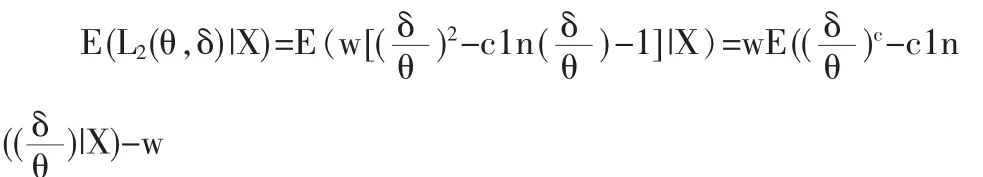
下证唯一性：欲证唯一性，只要证 r(δMMLE)＜+∞，由题设 r(δ)＜+∞，而 r(δMMLE)＜r(δ),故引理得证。

证明：设参数θ具有Jeffery’s无信息先验密度：π（θ）由（4）式知 θ｜X～Gamma(r,T)

故由引理3有

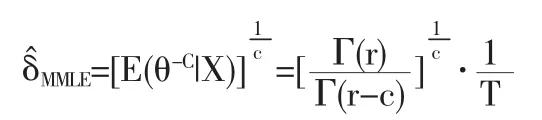
引理5[11]（Lehmann定理）在给定的bayes决策问题中，D为非随机化决策函数类，假如δ*∈D为对应于先验分布π*(θ)的 Bayes 估计，且其风险函数 R(δ*，θ)=ρ（常数），则 δ*为θ的Minimax估计。

2 主要结论

定理1 设X1,X2,…，Xn为来自分布密度为（3）式的一个简单随机样本，X（1），…，X(r)为前 r个次序统计量，r(≤)为首次失效时间

证明：首先我们要找到θ的Bayes估计,然后如果我们若能证明d的风险函数是常数，那么我们由引理5就直接得到定理的结论。下面我们假定参数θ具有Jeffery’s无信息先验密度那么给定样本x后参数θ的后验概率密度为：

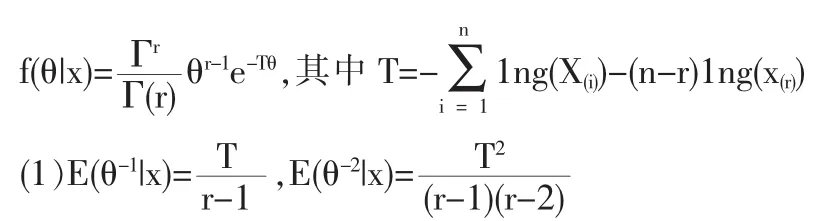
又由 T～Gamma(r,θ), 有

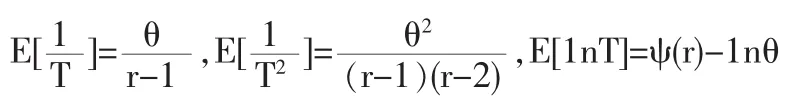
（2）由引理 4 有：

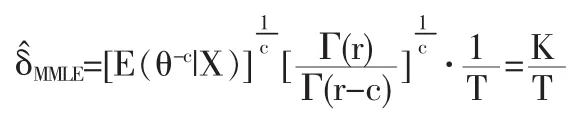
又

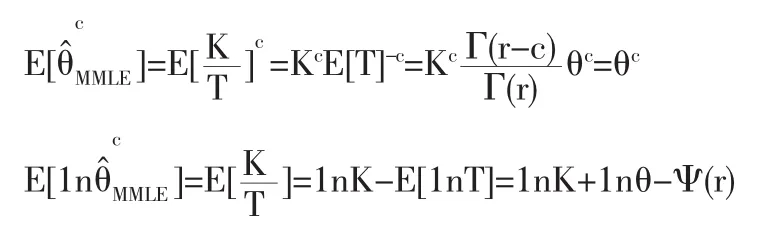
故有

3 数值模拟比较

采用均方误差(MSEs)对上述两个Minimax估计及极大似然估计进行比较。一个参数的估计的均方误差定义为：

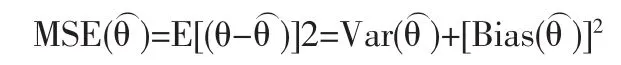
我们以指数分布 F(x)=1-[g(x)]θ=1-e-θx,θ=1 为例， 通过Monte-Carlo模拟，分别在不同的样本容量下，计算这三种估计的值及相应的均方误差。 记(n,r)表示(样本容量,截尾数)

(1）由表1可以看出，在 r＜25 时 ，加权平方损失函数下的极小极大估计的均方误差比极大似然估计和MLINEX损失函数的要小，在r较大(r>25)，上述三种估计的均方误差近似相等，且随着r的增大，这三种估计值之间的差异逐渐缩小。建议对于定数截尾试验的截尾样本数尽量多一些。

(2)经过多次数值模拟知，上述三种估计值相对于真值的近似效果与r,n以及样本观测值之间的差异有关，并且有时会对估计值产生较大的影响。

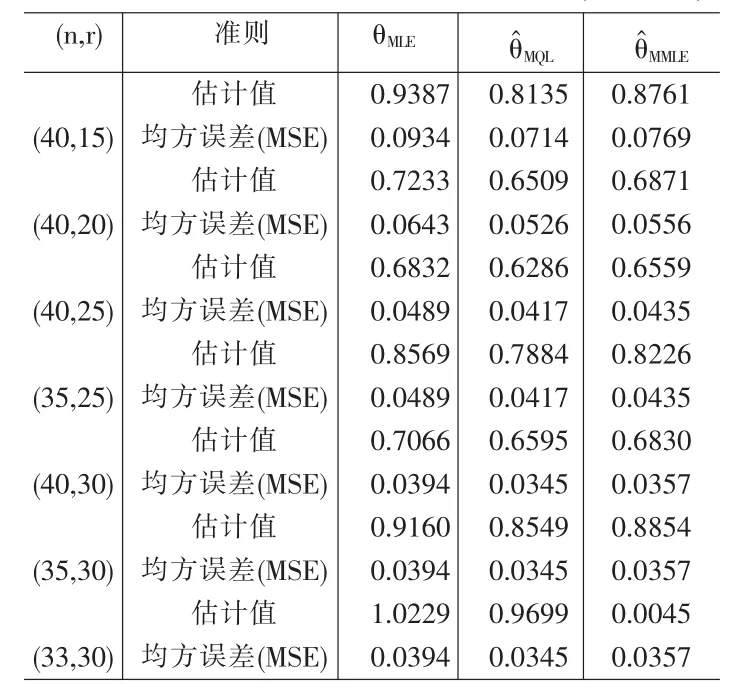
表1 三种不同估计的估计值和均方误差值(θ=1，c=1)

[1]Podder C K,Roy M K,Bhuiyan K J,et al.Minimax Estimation of the Parameter of the Pareto Distribution for Quadratic and MLINEX Loss Functions[J].Pak.J.Statist.,2004,20(1).

[2]Podder,C.K.Comparison of Two Risk Functions Using the Pareto Distribution[J].Pak.J.Statist，2004,20(3).

[3]Sanku Dey.Minimax Estimation of the Parameter of Rayleigh Distribution under Quadratic Loss Function[J].Data Science Journal,2008,7(23).

[4]Mahmoodi E,Sanjari F N.Minimax Estimation of the Scale Parameter in a Family of Transformed Chi-square Distributions under Asymmetric Quares Log Error and MLINEX Loss Functions[J].Journal of Sciences,Islamic Republic of Islamic,2006,17(3).

[5]Alicja Jokiel-Rokita,Ryszard Magiera.Minimax Estimation of Probability of Success under LINEX loss[J].Stat Comput,2007,(17).

[6]Alicja Jokiel-Rokita,Ryszard.Minimax Estimation of a Cumulative Distribution Function by Converting to a Parametric Problem[J].Metrika,2007,(66).

[7]Basu A P,Ebrahimi N.Bayesian Approach to Life Testing and Reliability Estimation Using Asymmetric Loss Function[J].J.Statistical Planning&Inference,1991，29.

[8]R.Calabria,G.Pulcini.Point Estimation under Asymmetric Loss Functions for Left-truncated Exponential Samples[J].Communications in Statistics Theory and Methods,1996,25(3).

[9]韩慧芳,杨珂玲,张建军.Pareto分布中形状参数的估计问题[J].统计与决策,2007(24).

[10]茆诗松.贝叶斯统计[M].北京:中国统计出版社，1999.

[11]Lehmann E L,George Casella.点估计理论（第二版）[M].郑忠国，蒋建成，童行伟,译.北京:中国统计出版社,2005.