多应急点资源优化调度模型研究

魏国强，景 琳

(江南大学 理学院，江苏 无锡 214122)

0 引言

突发事件是指危害人民生命财产、社会安全与稳定而突然爆发的事件，它具有破坏性、不确定性、突发性和紧急性。突发事件应急管理就是在突发事件的爆发前后,用科学的方法对其加以干预和控制,使其造成的损失减少到最小。事发前的资源布局与事发后的资源调度是应急资源管理的主要内容[1,2,3]。

本文拟研究这样的应急资源调度系统：突发事件发生后，应急点产生一定量的资源需求，这些源资需从多个存贮应急资源的出救点调运。仅当所需求的全部资源到达后应急工作才能开始。实际中不乏这样的情形：应对某些自然灾害及恐怖袭击时，若在人员装备数量不达最低标准的情况下仓促应战，不仅于事无补，且可能造成更大损失。此类方案首先要保证应急尽早开始，其次是要求出救线路数及出救点数尽可能少，以节省出救成本、提高出救可靠性。文献[1，2]研究了多出救点单应急点的此类问题，在出救时间为确定与模糊两种条件下给出了问题解法。

实际中经常要在同一时间应对不同地点的突发事件，资源调度方案由单应急点推广到多应急点在所当然。但将文[1]所建立的初等模型推广到多应急点情形将会遇到实质性困难。为此，本文拟首先建立两目标混合整数规划，解决单应急点的资源调度问题，再将此模型推广到多应急点的情形。新模型将试图解决更为一般的问题，且选择方案标准更切合决策者的要求，如可区分各应急点的权重求开始应急时间；既可最小化出救点数也可最小化出救线路数。

1 单应急点资源优化调度模型

本节建立、求解单应急点资源调度的混合整数规划模型，旨在为建立多应急点模型提供准备，同时丰富应急资源管理的理论。

1.1 问题描述及假设

突发事件发生后，应急点A对某种应急资源的需求量为x(x>0)；n 个存储应急物资的可出救点分别 A1，A2,…,An；岀救点 Ai的可供应资源量为 Si（i=1,2,…,n）， 满足资源从Ai到A 的运输时间时间为ti(i=1,2,…,n)，为方便见假设t1≤t2≤t3…≤tn。本节考虑单种资源调度问题，且假定全部应急资源到达后应急才能开始，不考虑分阶段调度。应急资源调度方案包括确定参与应急的出救点及从各点运出的资源数量，以满足应急需求为条件,本着提高应急效率、节约应急成本的目的，在应急开始时间最早前提下，使出救点最少。

1.2 建立模型

设xi为岀救点Ai的资源实际调度量；0-1变量yi当xi>0时取 1， 否则取 0；xi、yi为决策变量，yi由 xi决定；T 为全部资源到达后的应急开始时间。建立模型（M1）如下:

模型中含应急开始时间最早与参与应急点数最少两个目标。约束条件中，第一式为各应急点资源需求约束；第二式中的ε是充分小的正数，此式为各出救点设立资源量约束，并确保yi取1当且仅当xi>0；第三式与第一目标结合求min max{ti|yi=1}，实现应急开始时间优化的功能。

这是一个两目标混合整数规划模型。为及时高效地处置突发事件，调配应急资源应争分夺秒，因而时间是第一目标；在满足时间最早的前提下尽可能减少应急成本，可见出救点最少是第二目标。据此，此模型可用目标规划法求解。

1.3 算例1

地区发生突发事件，急需50吨某种物资(x=50),可从15个出救点调运。有关参数列于表1，要求资源优化调度方案。

表1 各出救点数据

在模型M1中先取第一目标编写lingo程序，求解得应急最早开始时间为 8；出救方案为：分别从 A1，A2，A3，A4，A6，A7依次调运资源 5，10，3，6，12，14。

再以应急开始时间=8为约束，以出救点数最小化为目标，计算得出救方案为分别从 A2，A3，A5，A6，A7依次调运资源10，8，7，12，13，出救点减少为 5。

2 调运时间为确定的多应急点资源调度模型

2.1 模型

设出救点 Ai的资源存量为 si（i=1,2,…,n）；B1,B2,…,Bm为m个应急资源需求点，dj为应急点Bj所需资源量 （j=1,2,…,m），并有资源从Ai运到Bj所需时间为 tij。 要求满足各应急点资源需求的调度方案，使各点应急开始时间最早，并在此前提下使出救线路及出救点最少。

设xij为由点Ai向点Bj的资源实际调运量；yij当xij>0时取1，否则取0；应急点Bj的应急开始的时间Tj满足下式

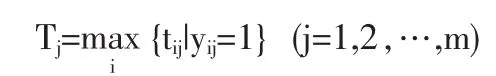
建立模型(M2)如下：

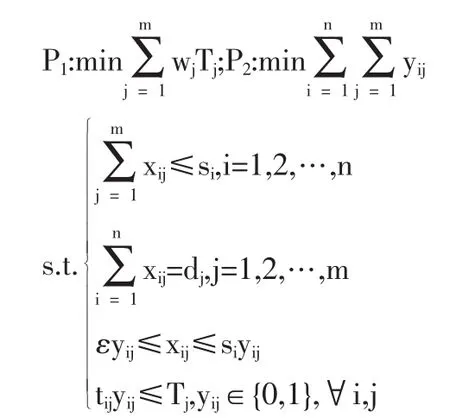
模型中wj是应急点Bj的重要性权重(j=1,2,…,n),第一目标是加权意义下的各点应急开始时间最早；第二目标是出救线路数最少。约束条件意义如下：第一式是各出救点的输出资源约束；第二式是各应急点资源需求约束；第三式确保0-1变量yij取1，当且仅当xij取正值；第四式与第一目标结合，确保得到加权意义下的各点应急开始时间最早调度方案。

2.2 算例2

某地区发生突发事件，有5个点同需某种资源应急。这些资源可从10个出救点调度。各出救点Ai已储备资源量、各应急点Bj所需资源量及Ai到Bj所需运输时间tij列于表2

（1）取模型M1的各应急点权重全为1，以第一目标与约束条件构成单目标规划，编程求解此模型得到：各应急点最早应急开始时间依次为3，4，4，3，2；加权开始时间和为16；调运线路11条；选中的应急点为8个。调度方案在表2中标出，如表中表示由A2向B2调运资源量3个单位。

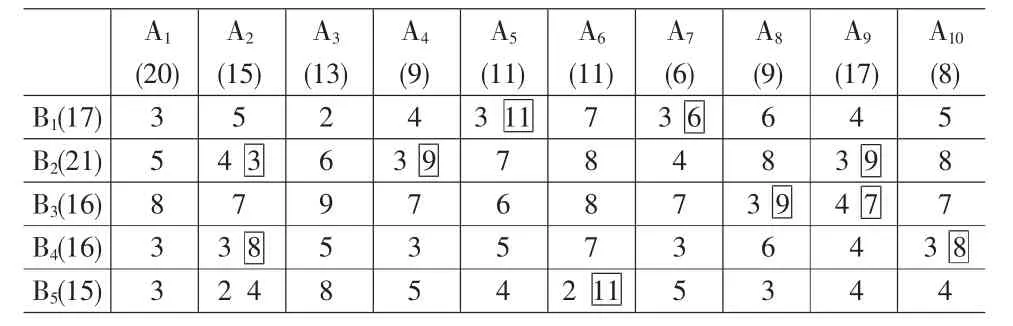
表2 算例2数据及应急最早开始方案

（2）将加权最早开始时间和为16加入原有约束构成新的约束条件，以总调运线路数最少为目标构模，并求解此模型。此时调运线路数由11减为9，出救点为8个；调度方案列于表3，如其中第2行第4列的13表示由A3向B1调运资源13个单位。

（3）求解2.1中所述最早应急开始时间条件下应急点最少模型，所得调度方案见表3，其中加框数据为调运量。可见出救线路没有增加，而出救点个数已减为6，且这些点全部资源用于应急，可实现成本的节约。

3 调运时间为区间数的多应急点资源调度模型

3.1 模型

由于突发事件的客观或人为因素，应急系统的资源运输时间具有不确定性，因而用区间数表示该时间更符合实际。假设应急资源从Ai到Bj所需运输时间为区间数tij=[tij1,tij2]，其余条件与上节相同。 由决策者根据事件应急的实际需要,给出点Bj的应急最迟开始时间tj，对每条运输路径及给定的tj，用真度aij刻划资源于tj前到达的可能度[4]。aij可按下列定义求出

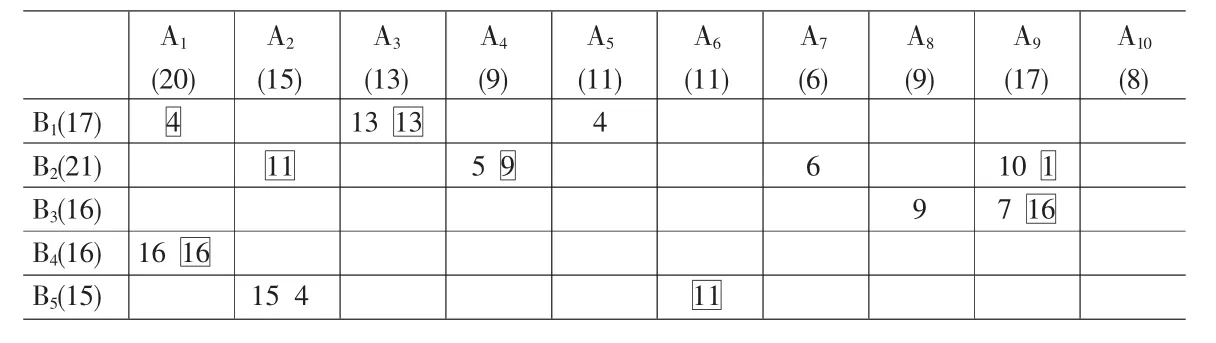
表3 算例2线路及出救点最少调运方案

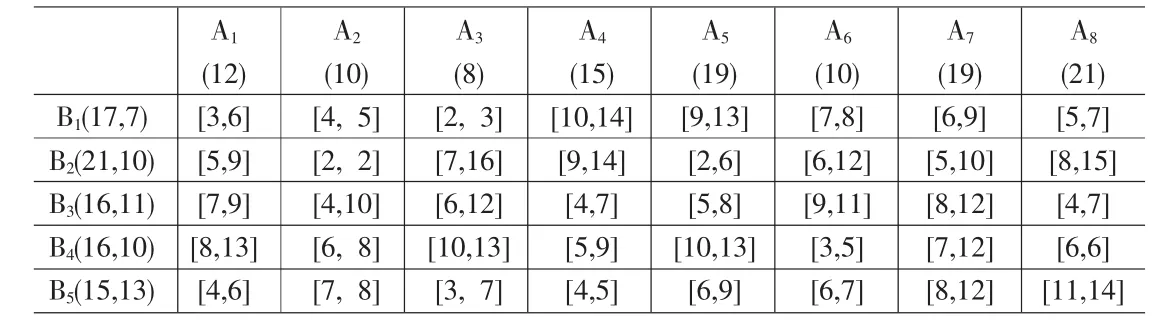
表4 算例3数据

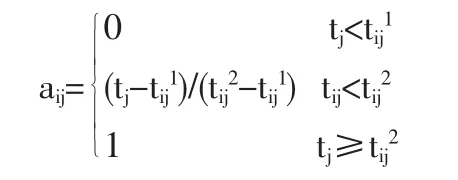
应急点Bj的所需应急资源于tj前全部到达的真度为要求满足各应急点资源需求的调度方案，使各点在规定时间内应急开始的真度最大，并在此前提下使出救线路及出救点最少。建立如下模型(M3)：

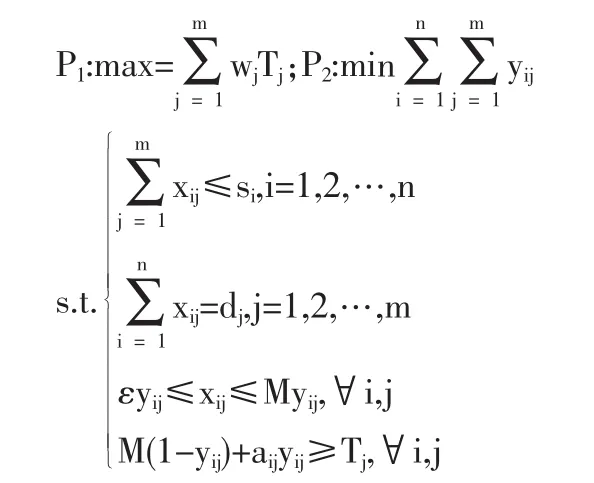
其中ε是充分小的正数，M是充分大的数；Tj为Bj于tj前应急开始的真度。

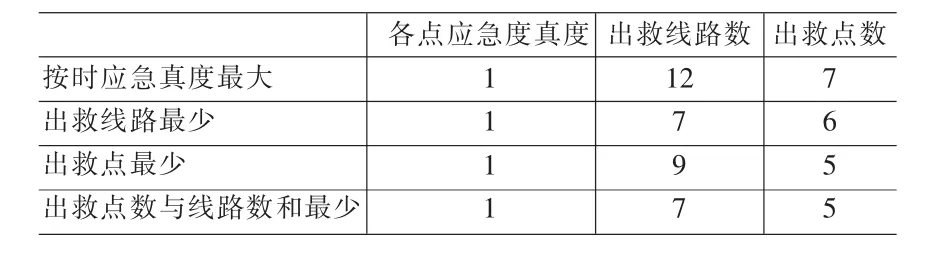
表5 各模型求解效果比较

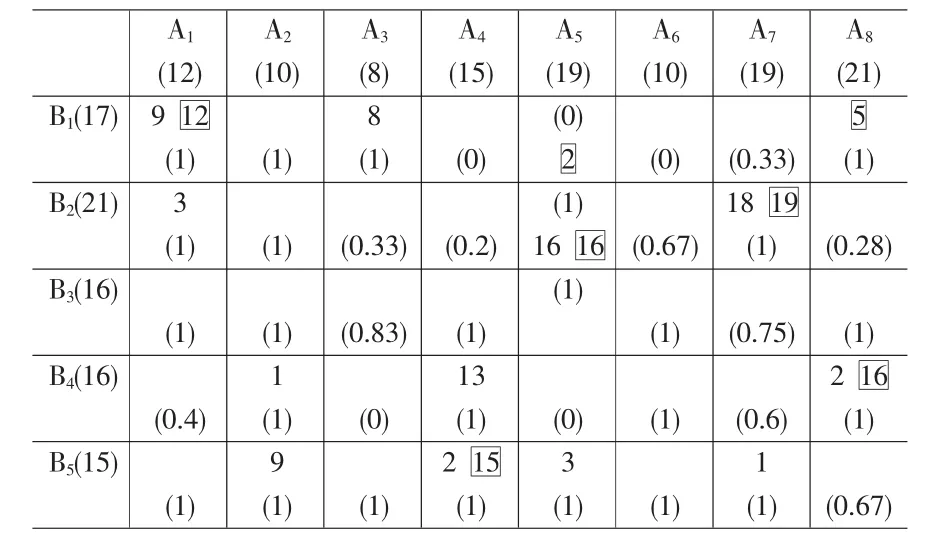
表6 算例2数据及应急最早开始方案

模型的第一、二目标分别为各点真度加权和为最大、出救线路最少；约束条件前三式意义同M2；第四式当yij=1时为Tj≤aij，而当yij=0时由于M是充分大的数，不等式总成立，此约束与目标函数P1结合，其作用是求即各应急点在规定时间内开始应急的真度最大。这是混合整数两目标规划模型。

3.2 算例3

某地突发事件发生，道路遭损坏及交通堵塞等原因造成运输时间不确定[5,6]。经综合各种信息估计出运输时间区间数，有关参数列于表 4，其中首列为（Bj,tj）数据，首行为（Ai，Si）数据；其余为区间数tij数据。据此算出各候选线路按时应急真度aij列于表5。

先以各点应急真度加权和最大为目标求解模型，再在保证以上目标最优值的前提下分别求得出救线路数最少、出救点数最少、（出救线路数+出救点数）最少的调度方案。结果表明：分别以真度加权和最大及（出救线路数+出救点数）最少为第一、二目标，按目标规划法求解效果最好（详见表5）。资源优化调度方案列于表6，表中位于2行第2列单元格的“(1)、9、”分别表示真度a11=1、在第一目标下调运量x11=9、满足第一目标前提下第二目标优化调运量x11=12。其余数据意义类推。

[1]刘春林,何建敏.多出救点应急系统最优方案的选取[J].管理工程学报,2000,(1).

[2]刘春林,盛昭瀚.基于连续消耗应急系统的多出救点选择问题[J].管理工程学报,1999,13,(3).

[3]魏国强.再论需求周期性变化的应急资源选址与配置[J].统计与决策，2009,(8).

[4]汪培庄,韩立岩.应用模糊数学[M].北京:北京经济学院出版社,1989.

[5]ReVelle C.S.,H.A.Eiselt.Location Analysis:A Synthesisand Survey[J].European Journal of Operational Research,2005,165(1).

[6]Barbarosoglu G.,Y.Arda.A Two-Stage Stochastic Programming Framework for Transportation Planning in Disaster Response[J].Journal of Operational Research Society,2004,(55).