概率神经网络在判别分析中的比较优势

米帅军，习 勤

（华东交通大学 经济管理学院，南昌 310003）

判别分析是用于判断样品或个体所属类型的一种统计分析方法。采用这种分析隐含的一个最为基本的假设是：已知总体按着某些特征或指标分为两个或两个以上的类型。从这个基本假定可以看出：一是总体划分类型的特征或指标必须为两个以上，如果只有一个指标，则很容易根据新抽取样品的指标值判断该样品属于哪一类；二是所分的类型中都必须包含一个或以上的个体，否则该类型是不可识别的[1]。在生产、科研和日常生活中就是根据总体的经验分类，结合样品调查的数据来对样品进行归类的。如根据客户的信用指标（房产、年龄、收入、职业、婚否等）来对信用卡客户进行信用评级，根据上市公司业绩表现等财务指标判别一个上市公司股股票类型。当然这里隐含了一个假设是：已知各类型客户或公司的评价指标值。从上述分析可以看出，判别分析适用于被解释变量为属性变量（如类型、等级、规格等），解释变量为可测量或可量化的统计分析。

1 问题的提出

常用的判别分析方法有距离判别法、贝叶斯判别法、费希尔判别法、逐步判别法，序贯判别等。这些判别分析方法都基于一定的假设条件。当假设条件与实际情况相差较大时，就会导致较高的误判率，尤其是类与类之间的特征（如均值）在统计上显著性不高时，误判率将急剧上升。

现以距离判别法、贝叶斯判别法、费希尔判别法为例来说明其应用的假设条件与基本思想。

1.1 距离判别法

距离判别法的基本思想是：样品和哪个类型的距离最近，就判断它属于哪个类，因而距离判别法又称直观判别法[2]。距离判别法分为欧氏距离判别与马氏距离判别，其差别是马氏距离采用了协方差阵来对距离进行校正。现以马氏距离判别法来说明其应用条件。为叙述方便，以总体分为两个类型为例。

马氏距离定义：设总体G有m个评价指标，均值向量为u=(u1,u2,…,um)'，协方差阵为∑=(aij)m×m，则新抽取的样品 X=(x1,x2,…,xm)'与总体G的马氏距离为：

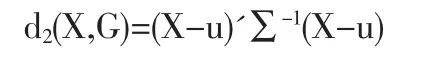
如有两个总体被分为两类G1、G2，则样品X=(x1,x2,…,xm)'与G1、G2的距离分别为：

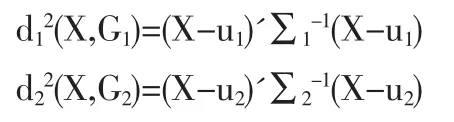
u1，u2，∑1，∑2分别为类 G1、G2的均值向量与协方差阵。

马氏距离的判别规则为：

(1)如果 W(X)>0，则 X 属于类 G2；

(2)如果 W(X)＜0，则 X 属于类 G1；

(3)如果W(X)=0，则有待用其它方法判定。

从马氏距离的判别函数可以发现，当类G1、G2的均值向量u1,u2，有显著性差别时，判别效率将较高；反之，则效率较低。事实上，由于u1，u2是m维向量，直观上很难判断u1，u2是否有明显差别。如果u1，u2并没有显著性差别而采用距离判别法将导致误判。

1.2 贝叶斯判别法

贝叶斯（Bayes）判别法的基本思想是：假定对研究的对象已有一定的认识，常用先验概率分布来描述这种认识；然后抽取一个样本，用样本来修正已有的先验概率分布，得到后验概率分布，再结合误判损失函数，可以得出期望误判损失，使平均损失 ECM（expected cost of misclassification）最小的判别方法称为贝叶期判别法。

设总体G被分为G1、G2两类，密度函数分别为p1(x)、p2(x)，先验概率分布分别为 q1(x)、q2(x)，误判损失函数分别为c1(G2｜G1)、c2(G1｜G2)，误判概率分别为 p1(G2｜G1)、p2(G1,G2)，则样品 X误判的平均损失为：

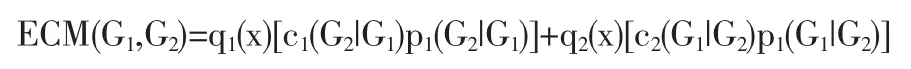
贝叶斯判别规则：如果把X判入G1的损失为ECM1，把X判入G2的损失为ECM2，则

(1)当 ECM1＜ECM2时，X 应属于 G1;

(2)当ECM1>ECM2时，X应属于G2;

(3)当ECM1=ECM2时，有待用其它方法判定。

从理论上来讲，贝叶斯判别很完善。与距离判别法相比，贝叶斯判别法克服了其两个不足：一是距离判别法没有考虑G1、G2出现的机会大小，即先验概率，这在进行异常类判断时很不合理，如信用卡恶意透支分析中将产生很大的偏差，因为恶意透支的概率相对较小；二是没有考虑误判的损失。

但是，贝叶斯判别法在实际应用中可操性不强。在实践中，除了能获得误判损失函数外，其它的参数与概率分布都是难以获得。通常的解决办法是假定总体的各类服从某一分布，一般取正态分布。事实上，在统计分析时假定正态分布前提是基于大样本。然而，大样本不仅与研究问题有关，且由于条件限制一般也难以取得足够大的样本。因此，如果概率分布假定与实际总体情况不一致将产生误判，误判率与分布概率偏差有正向关系。

1.3 费希尔判别法

费希尔判别的基本思想是投影，将总体G的G1、G2两类中的m维数据往某一方向投影，使得投影后G1与G2尽可能地分开。衡量投影后G1与G2是否明显地分开，采用一元方差分析[1]。

费希尔判别法很实用，与距离判别法一样，没有总体分布的假定。但是，与距离判别法相比，费希尔是基于协方差阵的矩阵线性变换，使两组G1、G2投影后尽可能地分开。

采用费希尔判别法也存在较高的误判率问题。事实上，在空间上分散的点，在投影后可能很靠近。因此，就一般的总体G而言，很难找到一个合适的投影方向使两组G1、G2投影后完全分开，即采用费希尔判别法易导致较高的误判率。

2 概率神经网络

人工神经网络是对生物神经网络进行仿真研究的结果。它通过采集样本数据进行学习的方法来建立数据模型，系统通过样本不断学习，在此基础上建立计算模型，从而建立神经网络结构[4]。神经网络通过训练后可以执行复杂函数的功能，能对所有函数进行逼近，即Universal Approximation Theorem[7]。这就是说，如果一个网络通过训练后呈稳定状态，那么神经网络就具备了执行输入到输出这种线性或非线性的函数功能。当然，这种函数不是基于理论或经验的假设，而是基于对样本的有监督的训练，使神经网络具备了模拟复杂系统的功能。概率神经网络是神经网络模型的一种，其网络模型结构图略。

概率神经网络（简称PNN）模型分为三层，第一层为输入层，第二层为Radial Basis Layer，第三层为Competitive Layer。输入向量为R，训练的样本数为Q（也即，共输入Q个向量R），每个目标向量有K个元素，因此，每个输入向量对应着K个元素中的一个。IW1，1是第一层的权重，是一个Q×R矩阵。

PNN的基本工作过程为：第一层计算输入向量与目标向量的距离，并形成一个新的向量，这个新向量显示了输入与目标输出之间的差别。第二层对每一个输入加权求和，并求每一个输入的贡献，并输出一个概率向量。第三层中的竞争转换函数从第二层的输出概率向量中挑出最大的概率值，使最大的概率对应某一类别[6]。

PNN适合于解决分类判别问题，可应用的领域相当广泛。只要有一定的样本量，PNN一定会收敛到一个贝叶斯分类[6]。但是PNN需要较多时间来计算分类，这是其一个不足之处。当然，如果PNN是用于经济分析而不是硬件产品设计，计算时间不足为虑，重要是它能得出更为准确的结果。采用PNN的另一个不足是研究者不能得到一个基于样本训练出来的分类判别函数，也即不能对输入输出进行结构分析，这也是所有神经网络模型的一大缺憾。

3 判别效率的比较与分析

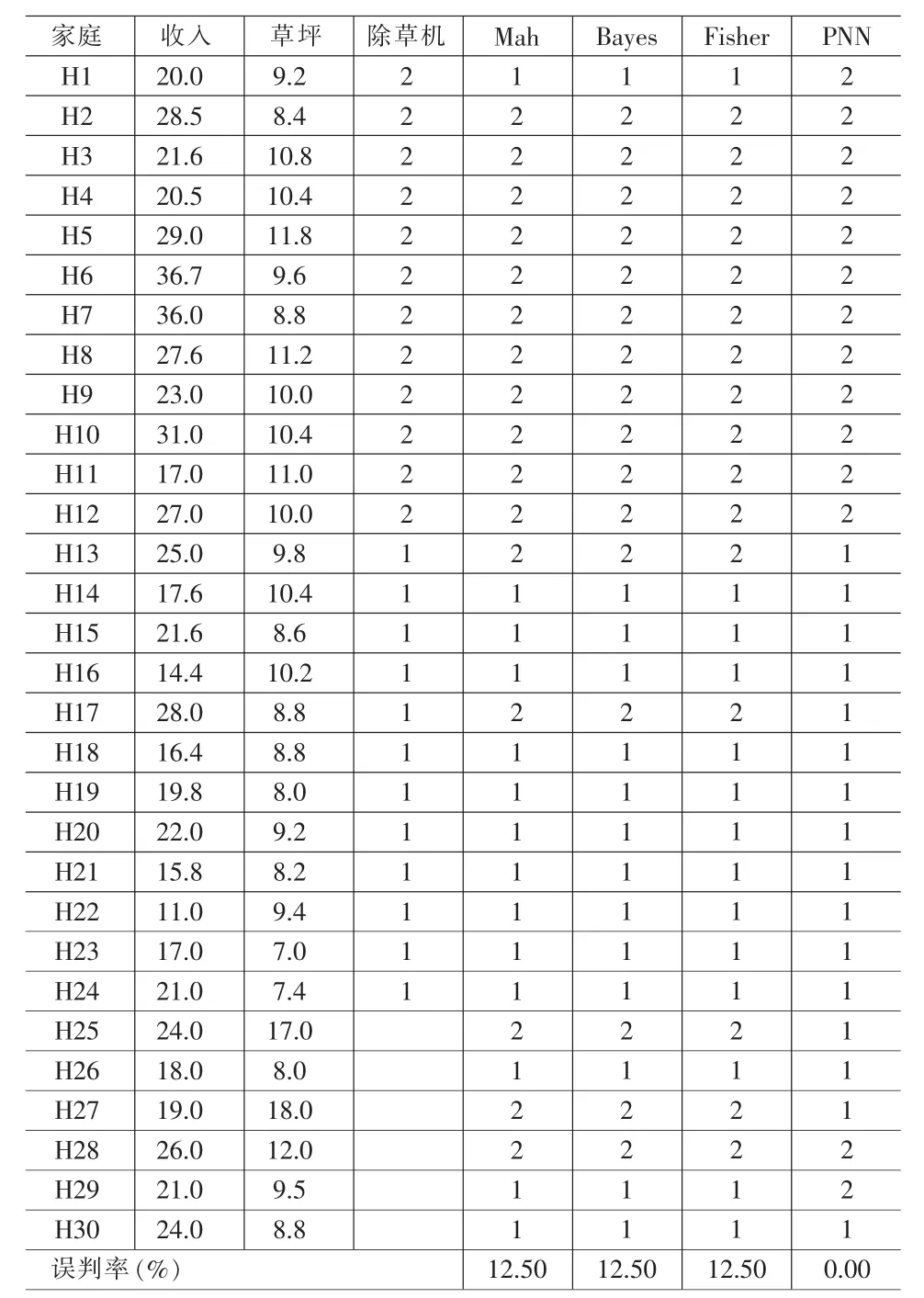
表1 家庭除草机数据的不同判别方法效率比较

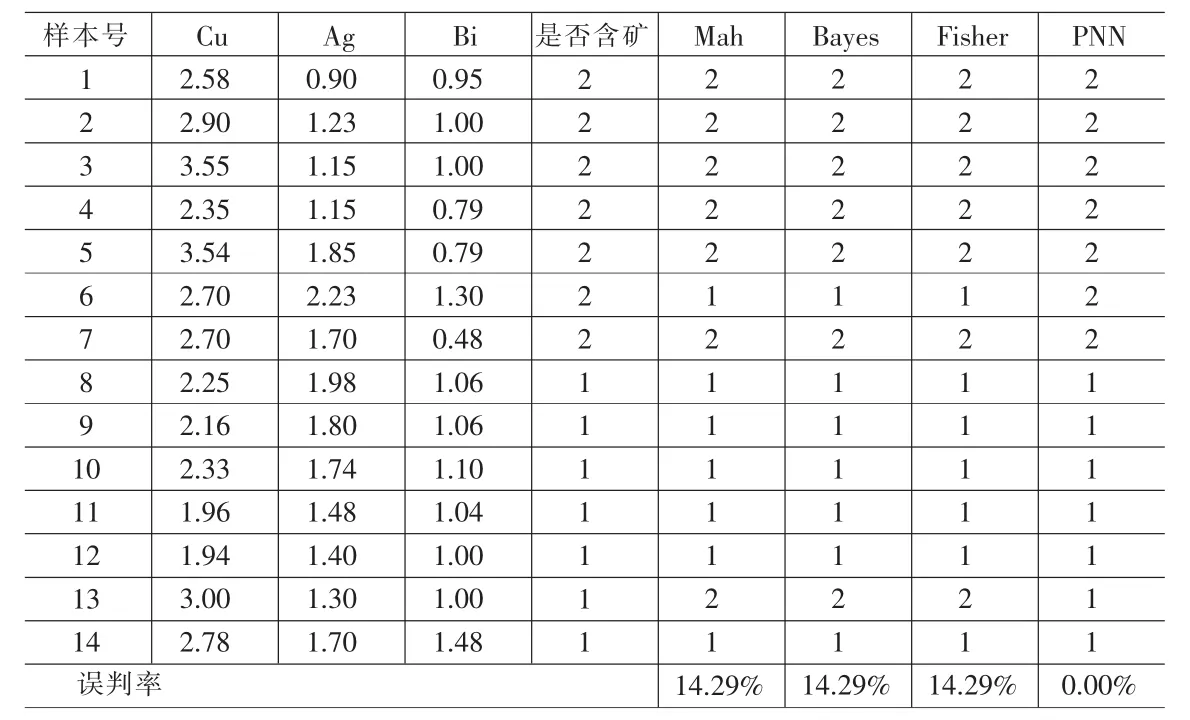
表2 岩石化学成分的含量数据的不同判别方法效率比较

本文用两个案例来比较上述判别方法的效率。采用的分析软件是SAS9与MatLab7（数据来源于参考文献[1]与[2]）。

案例一说明：有一个关于家庭拥有除草机与家庭收入、草坪面积的调查表，如表1所示。第H1至H24为调查数据，第H25至H30为预测对象，即通过判别分析，推测家庭H25至H30是否将购买除草机或已拥有除草机。分别采用距离判别法、贝叶斯判别法、费希尔判别法与PNN判别法。分析结果如表1所示。

从分析的结果来看，采用距离判别分析、贝叶斯判别分析、费希尔判别分析，对家庭H1、H13、H17是否拥有除草机产生了误判，误判率为12.5%，而采用PNN判别法误判率为0.00%。同时，对家庭H25、H27、H29的是否准备购买或拥有除草机的预测上也不同。

为了显示PNN的判别分析的优势，再列出一判别分析案例（仅给出判别分析结果，见表2）。

4 结束语

本文通过对PNN在判别分析中的比较优势进行简单地对比发现，对大样本的判别分析时，采用PNN优势更加明显，尤其是对于评价指标有几十个以上时，PNN更加凸显其模式识别的特有优势。如对基金评级、信用卡评级、上市公司业绩评级等可以采用更多的相关指标，以便从不同的侧面与角度来给出综合评价。同时，采用PNN评级可以有效地避开采用主成分分析等多元统计手法，因为在采用多元统计分析方法时，对指标进行压缩或组合会导致总体信息的损失。因此，如果只考虑类型的判别，而不进行结构分析，即不需要分析各个指标对评价目标的影响程度或权重时，采用PNN判别分析是完全合理的。由于PNN能对所有线性或非线性动态系统进行模拟，采用PNN进行判别分析的准确度相比而言是很高的。由于PNN是一个类似于黑夹子的模型，导致其对经济结构的解释不足。

[1]何晓群.多元统计分析[M].北京：中国人民大学出版社，2004.

[2]高惠璇.应用多元统计分析[M].北京：北京大学出版社，2005.

[3]丛爽.面向MATLAB工具箱的神经网络理论与应用[M].北京：中国科学技术大学出版社，1998.

[4]张云涛，龚玲.数据挖掘[M].北京：电子工业出版社，2004.

[5]岳朝龙，黄永兴，严忠.SAS系统与经济统计分析[M].北京：中国科学技术大学出版社，2003.

[6]H Demuth.MATLAB Neural Networks Toolbox，Probabilistic Neural Networks[M].Mathworks Inc，1993.

[7]Simon Haykin.Neural Networks：A Comprehensive Foundation（2ndEdition）[M].北京：清华大学出版社，2001.