逆抽样条件下含结构零的2×2列联表中相对差的估计
2010-07-23江绍萍
江绍萍
(1.云南民族大学 数学与计算机科学学院,昆明 650500;2.云南大学 数学与统计学院,昆明 650500)
0 引言
在实际生活中,研究者经常遇见这样的一类问题,即在2×2列联表的对角线上有一个元素为零;且在理论上,这个为零的格子在试验中是观察不到次数的,故含结构零的2×2列联表就产生了。如1997年日本进行结核病的临床试验[1]称为TB试验,总共进行两次TB试验。在第一次TB试验后,都希望被试验者呈强阳性(Positive也就是有肺结核抗体)。过一到三周后在进行第二次TB试验,若第一次试验后呈阳性反应的患者将不进行第二次TB试验。经过第二次TB试验后,患者还是出现阳性或者阴性的反应,从而得到含结构零的2×2列联表。这个试验中,试验的总样本数是固定的,若样本数小,那么可能使得其它三个格子中的样本数为零。为了避免这种情况的发生,在试验中加入了逆抽样过程。
逆抽样(又称为负二项分布)即为连续抽样直到获得先前固定的r个感兴趣的样本时才停止抽样。在现实生活中,逆抽样条件下相对差的估计问题具有很高的实用价值。所以一些学者已作过类似的研究,如KungJongLui[3,4,5]把逆抽样的思想加入到2×2列联表的研究过程中,他只是建立了Wald统计量和对数Wald统计量进行假设检验,且在求解得方法采用极大似然估计的方法求解感兴趣参数的估计及方差。M.L.Tang[4]作了逆抽样条件下两组独立的样本的风险比的检验问题。
1 概率密度函数及其相对差的定义
本文在含结构零的列联表中加入逆抽样,以检测结核病抗体的试验为例,即在TB试验中连续抽样,直到抽到先前固定x1(x1>0)的个第一次TB反应为阴性的样本时才停止抽样。我们得到如下的列联表的形式:

其中 0<πij<1(j=0,1)是列联表的相应格子中的概率,X11,X10,X00为落入相应格子的样本数。 并且满足:π1=π11+π10;π1+π00=1;X11=0,1,…x1;X10=0,1,…,x1;X00=0,1,…。 从而得到变量X=(X11,X10,X00)的概率密度函数为:
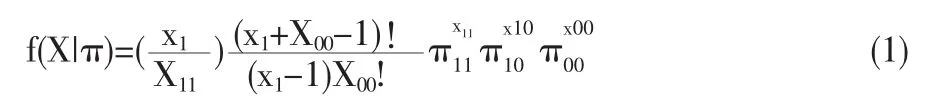
在含结构零的2×2列联表中,相对差的定义为:

根据相对差的定义,可以用参数δ和π1表示出其它的参数,即 π11=π1(π1-δ),π10=π1(1+δ-π1),π00=(1-π1)。 从而得到了由参数δ和π1表示的似然函数:
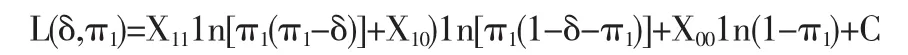
其中,C为不依赖于δ和π1常数,δ为感兴趣参数,π1为讨厌参数。
2 参数估计及其统计量的建立
本文感兴趣的是检验相对差δ是否等于先前固定的某一个值δ0,从而建立如下的假设检验问题:
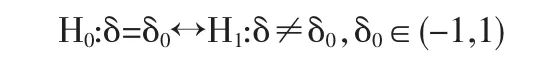

同理,可以求得在H0:δ=δ0条件下参数的极大似然估计,记为即求解如下方程:

得关于π1的一元三次方程:
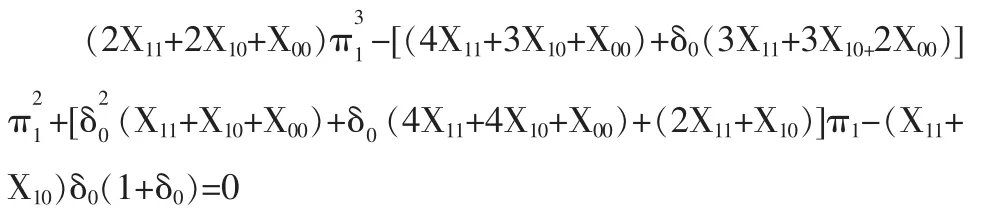
计算过程中采用一元三次方程的求根公式来求解上述方程组的根。
以往求解感兴趣参数的期望和方差,通常的做法是采用delta方法,但delta方法是一种近似求解的方法,得到的结果带有一定的偏差。为了避免出现偏差,本文采用Fisher-score的方法来求解参数的方差。由此建立Fisher信息阵如下:
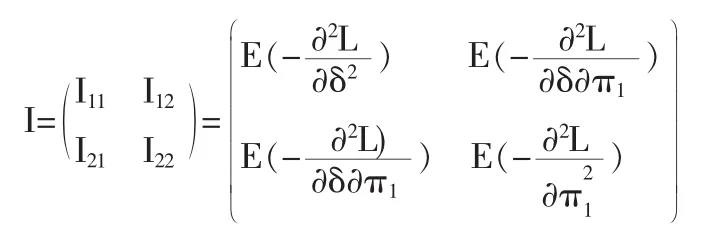
在求解Fisher信息阵的过程中应该注意到,变量X11服从参数为x11和π11/π1的二项分布;同理X10服从参数为x1和π10/π1的二项分布;而变量X00服从参数为x1和的负二项分布。故可以得到各随机变量的期望如下:

通过求解Fisher信息阵的逆矩阵得到感兴趣参数的方差为:
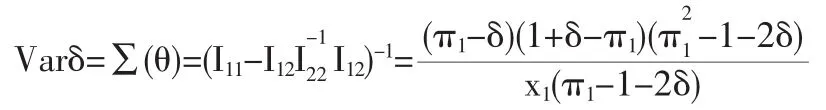
建立统计量如下:

3 模拟研究
在实际中,可以通过求解各统计量条件下犯第一类错误的概率和功效来检验建立的统计量的优劣性。并采用蒙特卡洛的方法对有限样本进行模拟。当给定了δ0和π1的值之后,通过相对差的定义得到 π11,π10,π00的值。 所以模拟的过程中, 相对差 δ0取值为-0.2,-0.1,0.0,0.1;π1取值为 0.3,0.5,0.7,显著水平为α=5%,得到相应的结果见表1、表2。

表1 统计量T1,T2,T3,T4条件下犯第一类错误的概率
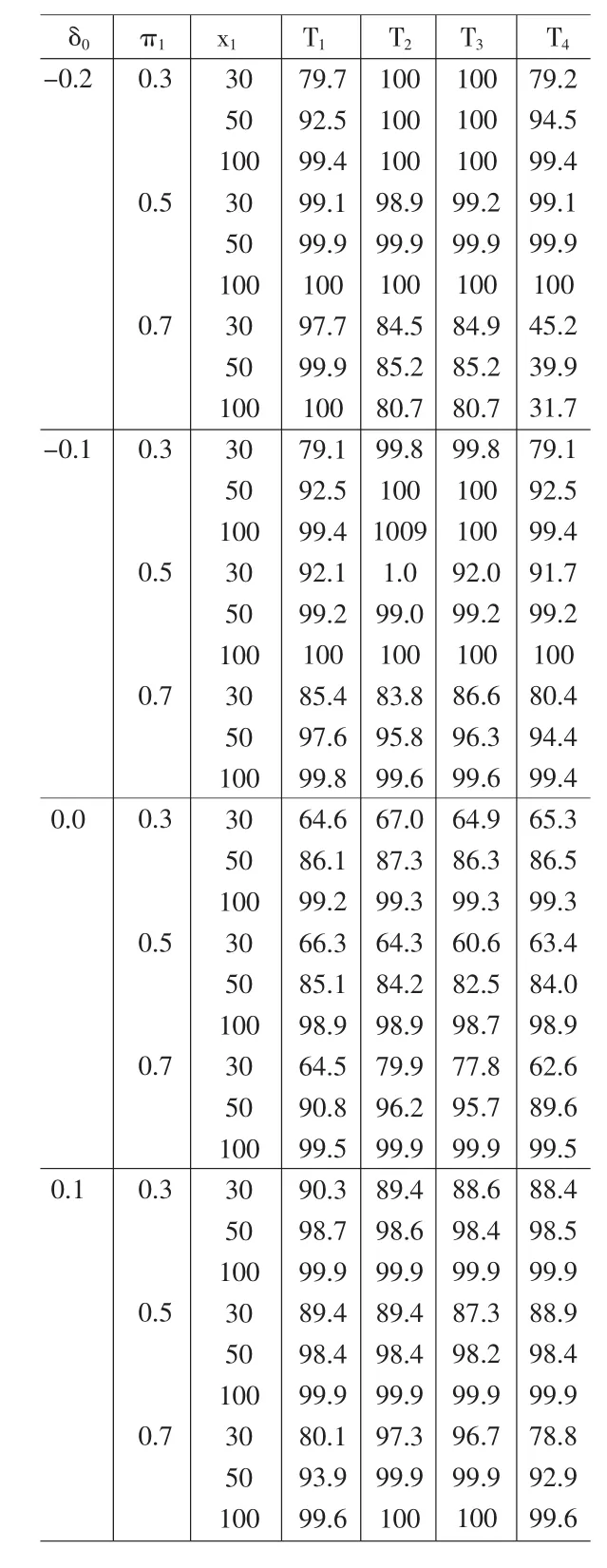
表2 统计量T1,T2,T3,T4条件下的功效
通过计算犯第一类错误的概率和功效,得到如下的结论:
观察表1、表2发现,Score统计量是最优的。因为在参数取值相同的条件下,它能保证犯第一类错误的概率最小且功效还能达到最大。
T3统计量即Wald-score统计量适用于处理大样本的情况。在T3统计量条件下,所求得的犯第一类错误的概率随着样本值的增大而减小,并趋近于置信水平。所求解得的功效随着r的增大而增大。
在模拟过程中,无论样本值r的取值如何,T2统计量即Score统计量都能使得犯第一类错误的概率达到最小,同时也使得功效达到最大。特别在样本值r小于30的情况下,犯第一类错误的概率接近于置信水平。随着样本值r的增大,功效变化不大。故可以T2统计量来处理小样本问题。
通过观察犯第一类错误的概率发现,T1统计量即Wald统计量比T3统计量性质更稳定一些,但是在相同的参数条件下,T1统计量求解得的功效比T3统计量差一些。
通过观察犯第一类错误的概率发现,T4统计量即似然比统计量的性质比较稳定,但是观察功效发现波动性比较大,不太稳定,所以T4统计量比其他的统计量性质要差一点。
4 讨论
现实生活中逆抽样的问题经常涉及到。本文除了应用逆抽样的方法外,还采用Fisher-Score的方法求解感兴趣参数的方差。这种方法可以比较准确地求解参数方差,避免了采用delta方法求解感兴趣参数方差时存在的误差。另外,文中建立了四个统计量,并讨论了这四个统计量所使用的条件,还得到了一个最优的统计量,为以后的研究提供了一个有用的方法。在以后的问题的讨论过程中,可以采用类似的方法讨论π11/π12的假设检验问题。
[1]Toyota,M.,Kudo,K.,Sumiya,M.,Kobori,O.High Frequency ofIndividuals with Strong Reaction to Tuberculosis among Clinical Trainess[J].Japanese Journal of Infectious Disease,1999,52.
[2]Nian-Sheng Tang,Man-lai Tang,Ivan Siu-Fung Chan.On Test of Equivalence Via Non-unity Relative Risk for Matched-pair Design[J].Statistics in Medicine,2003,22.
[3]Kung-Jong Lui.Estimation of Rate Ratio and Relative Difference in Matched-pairs underInverse Sampling[J].Environmetrics,2001,12.
[4]M.L.Tang,Y.J.Liao,H.K.T.Ng,P.S.Chan.Testing of Rate Ratio under Inverse Sampling[J].Biometrical Journal,2008,89.
[5]Kung-Jong Lui.Point Estimation on Relative Risk under Inverse Sampling[J].Biometrical Journal,1996,38.
[6]Kikuchi,D.A.Inverse Sampling in Case Control Studies Involing a Rare Exposure[J].Biometerical Journal,1987,29.
[7]Kung-Jong Lui.Confidence Intervalsforthe Risk Ratio in Cohort Studies under Inverse Sampling[J].Biometrical Journal,1995,37.
[8]Kung-Jong Lui.Sample Size for the Exact Conditional Test under Inverse Sampling[J].Statistics in Medicine,1995,15.
