考虑随机利率因素的保费随机的复合Poisson风险模型

赵晓芹

（长沙理工大学 数学与计算科学学院，长沙 410004）

0 引言

古典风险模型是一个简化的理想模型，很多条件都是为数学上处理方便而假定的。模型中，保险公司在单位时间内按常数速度取得保单且每张保单的保费均为常数，同时得到的资金不运用，这显然不符合保险公司经营的实际情况。本文拟对古典风险模型作两方面的推广：一是保费随机收取。将保单到达计数过程推广为齐次Poisson过程，每张保单收入为一随机变量；二是考虑随机利率因素。在一般的风险理论文献中，利率常被设定为常数[1]～[5]，但是许多经济行为都是长期的，这期间政府政策、经济周期等因素都会造成不确定性，即会带来一定的风险，而未来利率的随机性决定保险公司的赔付能力估计和应急准备金计划，因此采用固定利率可能会带来与实际之间的较大偏差。为了更准确地反映这种不确定性，避免由考虑常利率产生的风险，一种较好的方法就是采用随机利率模型。文献[6]研究了一类随机利率模型，用概率论方法得到最终破产概率的表达式。本文将建立一类考虑随机利率因素的保费随机的风险模型，主要运用鞅方法，得到有限时间破产概率的一个上界及最终破产概率的Lundberg指数型上界估计。

1 模型的建立

定义 1 设 M={M(t);t≥0}，N={N(t);t≥0}分别是强度为 λ、α 的齐次 Poisson过程，{Xk,k=1,2,…}和{Yj,j=1,2,…}是两独立同分布的非负随机变量序列，其分布函数分别为F（x）和G(x)，均值分别为u1、u2。I为一离散型非负随机变量，分布律为P(I=ij)=pj,j=1,2,…，均值为 i。 假定 M，N，Xk，Yj，I相互独立，u为正的常数。令

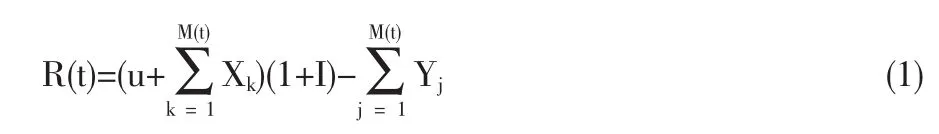
则式(1)中所定义的盈余过程为带随机利率的保费随机收取的复合Poisson风险模型。

实际背景：M(t)表示在时段(0,t]内保险公司收取的保单数，每张保单的保费额是Xk；N(t)表示在时段(0,t]内保险公司的理赔次数，每次的理赔额为Yj；I为随机利率，u为初始准备金。则R(t)为t时刻保险公司的盈余。令

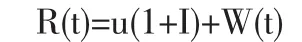
容易得到

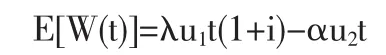
为了保证保险公司的稳定经营，通常假设E[W(t)]>0，从而能保证相对安全负荷为正。更进一步，还可以假定λu1(1+imin)-αu2>0，其中imin是随机利率I所有可能取的值中最小的值。

破产时刻定义为：

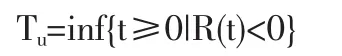
有限时间破产概率为：

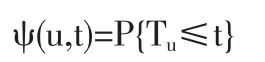
最终破产概率为：

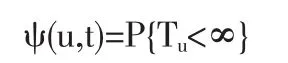
令

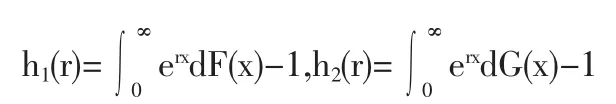
2 有限时间破产概率的一个上界

首先可以得到:

所以：

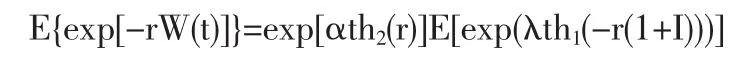
容易看到，盈余过程{W(t);t≥0}是一个右连续过程，具有独立增量性。对于盈余过程{W(t);t≥0}，任意给定r>0，0≤s≤t，有

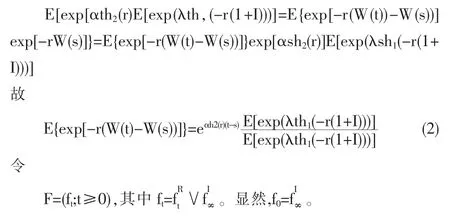
定理 1 {R(t)-ER(t);t≥0}是 F-鞅。

证明：对于任意s≤t，由过程{R(t);t≥0}具有独立增量性，有

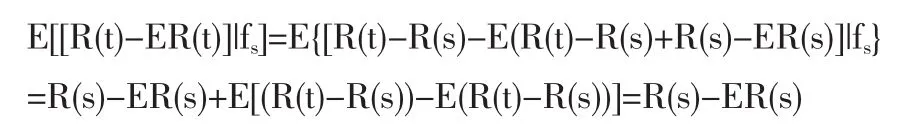
证毕。

定理2 令

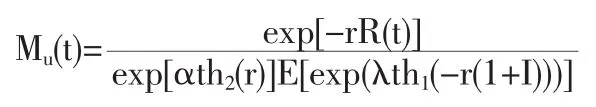
则 Mu={Mu(t);t≥0}是 F-鞅。

证明：对于任意s≤t，由独立增量性及式(2),得

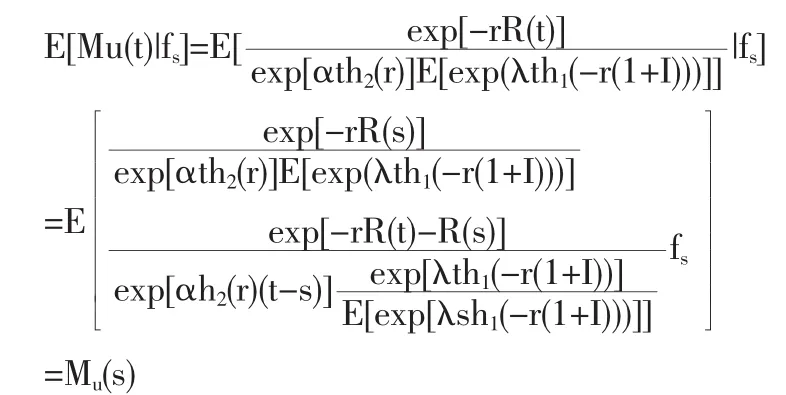
证毕。

引理1 设T是一个有界停时，M是一个右连续F-鞅，则有

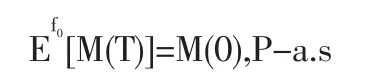
定理 3 ∀t，有

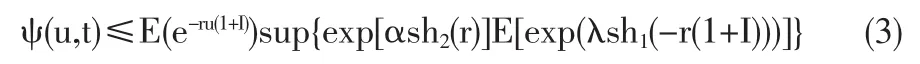
式中 r满足 r>0，h2(r)＜∞。

证明：由对函数hk(r)性质的假设知存在 r>0，使得 h2(r)＜∞，此时 h1(-r)＜∞，故由式(2)知，E{exp[-r(W(t)-W(s))]}＜∞。又由定理2知Mu是F-鞅。选取t＜∞，则t∧Tu是一个有界 F-停时。注意到而Mu是正的,所以由引理1得

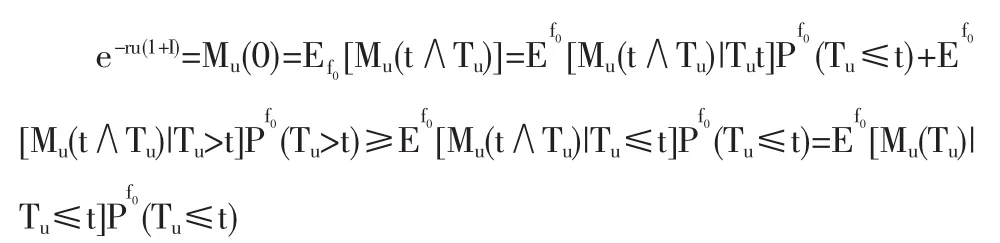
由于当 Tu＜∞ 时,R(Tu)＜0,故

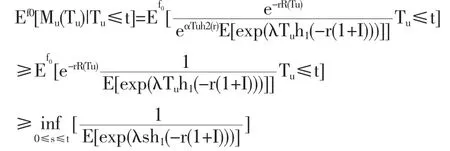
由此可得

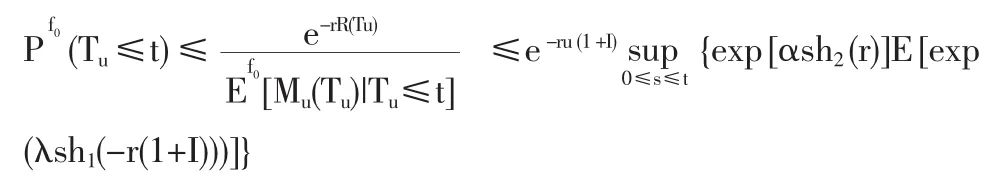
两边取期望,得有限时间破产概率

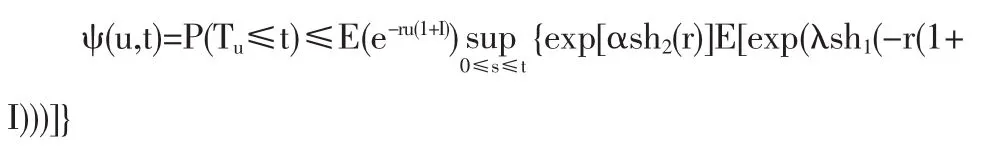
证毕。

依据有限时间破产概率的上界估计式,保险公司可以根据以往的历史资料,选择制定适当的险种和合理的保费,预留必要的准备金,以使得有限时间破产概率(比最终破产概率更接近实际的每一时期的破产概率)达到预想小的程度。

3 最终破产概率的Lundberg指数型上界估计

在式(3)中令t→∞取极限,得

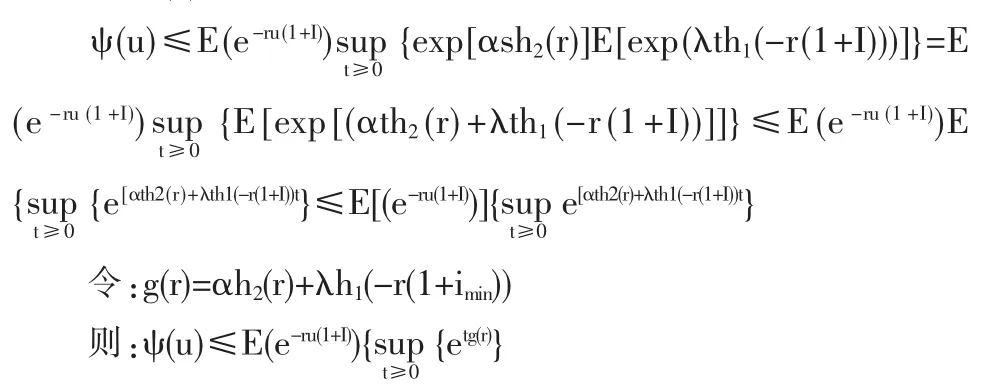
定义 2 令 R=sup{r｜g(r)≤0},称 R为盈余过程(1)的调节系数。

定理4 方程g(r)=0存在唯一正解R,即调节系数。

证明:易知

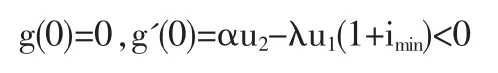
又g''(r)>0,故曲线g(r)是下凹的,而且limg(r)=+∞

故方程g(r)=0有唯一正解R。

由此可得最终破产概率的Lundberg指数型上界估计。

定理5 最终破产概率

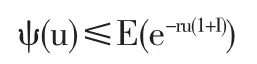
其中R为调节系数。

[1]Bjorn Sundt,Jozef L.Teugels.Ruin Estimates under Interest Force[J].Insurance:Mathematics and Economics,1995，（16）.

[2]Vladimir Kalashnikov,Dimitrios Konstantinides.Ruin under Interest Force and Subexponential Claims:a Simple Treatment[J].Insurance:Mathematics and Economics,2000,27.

[3]Ruud Brekelmans,Anja De Waegenaere.Approximating the Finitetime Ruin Probability under Interest Force[J].Insurance:Mathematics and Economics,2001,29.

[4]Dimitrios Konstantinides,Qihe Tang,Gurami Tsitsiashvili.Estimates for the Ruin Probability in the Classical Risk Model with Constant Interest Force in the Presence of Heavy Tails[J].Insurance:Mathematics and Economics,2002,31.

[5]张燕，田铮，刘向增.常利率下相依风险模型的破产问题[J].纺织高校基础科学学报，2007，20（4）.

[6]李晋枝，乔克林，何树红.随机利率因素的破产模型[J].云南大学学报（自然科学版），2003，25（1）.

[7]Grandell J.Aspects of Risk Theory[M].New York:Springer-verlag,1991.