资金约束和数量折扣下的零售商延迟支付订货策略

张义刚 ，唐小我

（1.西南财经大学 信息工程学院，成都 610074；2.电子科技大学 经济管理学院，成都 610054）

0 引言

传统经济批量订货模型(EOQ)的一个重要假设是零售商订货之后立即支付供应商货款。而在实际商业活动中，基于各种原因，零售商常常延迟支付(delay in payments)。Goyal[1]于1985年率先研究了延迟支付情况下的EOQ模型，之后许多学者对延迟支付下的订货策略进行了研究，其中的一个研究方向是假定供应商制定的商品批发价格与零售商的订货批量相关，即将延迟支付与数量折扣 (quantity discount)问题相结合。有关数量折扣下的EOQ模型，可见Das[2]、Tersine和Toelle[3]以及Goyal和Gupta[4]等的研究。结合延迟支付，Khouja和Mehrez[5]研究了4种付款方式下零售商的订货策略，其中一种为零售商的订货批量必须达到一定阈值才能享受延迟支付。Chung和Liao[6]研究了有订货批量阈值的延迟支付问题，考虑的是易逝商品。Huang[7]假设只有订货批量达到阈值才能享受全部商品的延迟支付，否则只有部分商品能够延迟支付。Shinn和 Hwang[8]从另外的角度研究了数量折扣问题，他们假定延迟支付期的长短与订货批量相关。

在已有的延迟支付和数量折扣结合的研究中，隐含了一个重要假设，即不管订货批量是多少，零售商在延迟支付期结束时总是有足够的资金支付给供应商。而事实上，零售商的决策会受到资金的影响。当订货周期大于延迟支付期时，零售商有可能在延迟支付期结束时无足够的资金支付供应商。也就是说，对于那些自有资金不充裕而且融资困难的零售商而言，其订货行为存在着资金约束。当数量折扣存在时，零售商有加大订货批量以获得较高折扣的需要，这时不能不考虑资金约束。

本文拟研究在资金约束、数量折扣和延迟支付均存在的情况下，零售商的最优订货策略。

1 模型假设及符号

1.1 问题描述及假设

供应商允许零售商延迟支付货款。对于不同大小的订货批量，供应商制定了不同的批发价格，但延迟支付期均一样。零售商订购商品的市场需求率恒定，不允许缺货，每一周期结束时零售商的库存为零，即零售商的订货环境符合EOQ模型的基本假设，零售商采用EOQ模型来订货。

零售商存在资金约束。尽管每一周期结束之后，零售商可以用获得的销售利润追加订货资金，但是，对于适合使用EOQ模型来订货的商品而言，其需求率是恒定的，其零售价格也波动不大，零售商在该项商品上可以获得的利润也相对有限。而且，零售商在另外的领域也可能需要资金。因此对于适合EOQ模型订货的商品，可以假定在每一个周期中，零售商存在着一个固定大小的投入资金限额，在需要向供应商支付时，零售商在该商品上投入的自有资金总额不能超过该限额，其余资金则通过该项商品的销售解决。

1.2 符号

D：商品的需求率(件/年)；

S：每次订货的订货费；

h：单位商品单位时间内的持有费；

T：订货周期；T*：最优订货周期；

Q：订货批量，Q＝DT；Q*：最优订货批量；

M：延迟支付期；

I：零售商单位资金的年利息收入；

c：商品的批发价。供应商实行数量折扣策略，即Q∈[qi,qi+1)时，c=ci(i=1,2,…,n；c1＞c2＞…cn)；

p：商品的零售价(p＞c)；

Y：零售商在该项商品订货中的资金限额；

Z：零售商的年总费用。

2 模型

零售商的年总费用=年货款+年订货费+年持有费-年利息收入

年货款=cD；年订货费=S/T

年持有费=hDT/2

年利息收入依赖于零售商订货周期和供应商给定的延迟支付期之间的关系。当订货周期由小变大时，会经历图1和图2所示意的两种情况。

2.1 T＜M

一个周期中的利息收入=IYT+IpDT2/2+IpDT(M-T)

年利息收入=IY+IpDT/2+IpD(M-T)

零售商的年总费用为

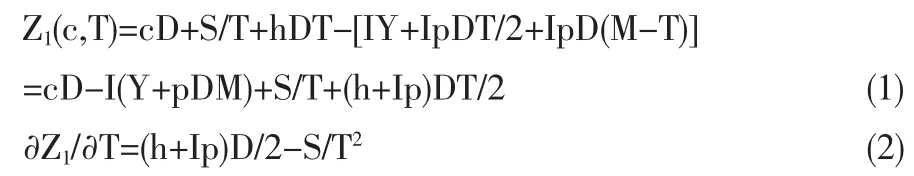
由∂2Z1/∂T2＞0，得在∂Z1/∂T=0 时年总费用最少。 因此最优订货周期为

最优订货批量为

2.2 T≥M

在一个周期中

|OM|时段利息收入=IYM+IpDM2/2

在M点，零售商必须支付货款cDT(包含的约束条件是Y≥cDT-pDM)，零售商的资金减少cDT，因此

|MT|时段利息收入=I(Y+pDM-cDT)(T-M)+IpD(T-M)2/2

年利息收入=(|OM|时段利息收入+|MT|时段利息收入)/T

=IY+IcDM+(Ip-2Ic)DT/2

因此年总费用

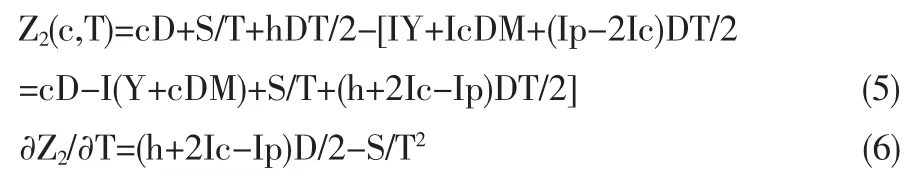
由∂2Z2/∂T2＞0，得在∂Z2/∂T=0 时年总费用最少，因此批发价为c时的最优订货周期为

最优订货批量为

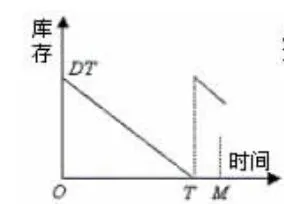
图1 T＜M

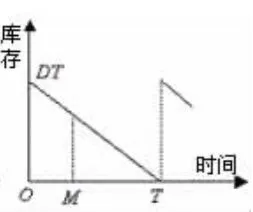
图2 T≥M

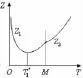
图3 情形①

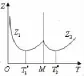
图4 情形②

2.3 零售商的最优订货策略

年总费用最少时，零售商的订货策略最优。因此零售商最优订货策略的确定，即是求解下面的规划问题。

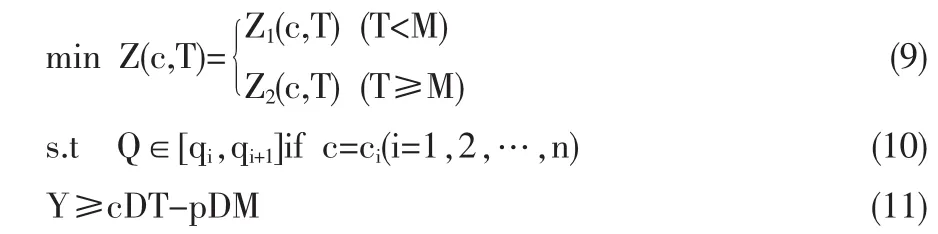
其中，式(10)为供应商的订货批量约束，式(11)为零售商的资金约束。

3 模型求解

3.1 模型讨论

下面，讨论零售商年总费用函数Z(c,T)的一些性质。基本思路是，将Z(c,T)看成是区间T＜M和T≥M上的分段函数，通过对函数性质的讨论来分析比较驻点和T=M处函数值的大小，进而寻找符合约束条件的最小总费用。

性质1 对于任意c，Z(c,T)在T=M处是连续的。

证明：对于任意c

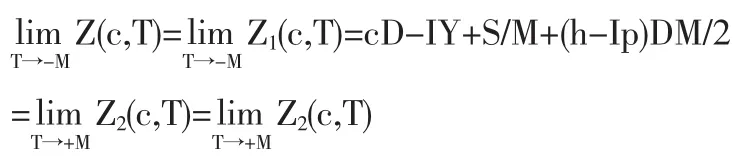
证明：由式(2)和(6)，有

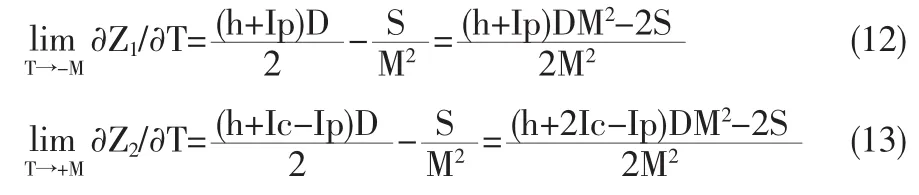
由 c＜p，得 2Ic-Ip＜Ip

由于∂2Z1/∂T2＞0 和∂2Z2/∂T2＞0，性质 2 意味着对于任意 c，Z1和Z2的组合只有3种情形(参见图3、图4和图5)。这就引出了下面的性质3。为了叙述的方便，在(12)和(13)式中，令

△1=(h+Ip)/DM2-2S；△2=(h+2Ic-Ip)/DM2-2S

由于分母为正，△1和△2分别决定了式(12)和式(13)与零的大小关系。

性质 3 ①当△1＞0，△2≥0 时，T*=

②当△1＞0，△2＜0 时， T*为和中与 min{Z1(c,),Z2(c,T2*)}对应者；

③当△1≤0，△2＜0 时，T*=。

证明：①△1＞0，△2≥0时的情形由图 3示意，因此最优订货周期T*=

②△1＞0，△2＜0时的情形由图 4 示意，因此最优订货周期T*为和中与min{Z1(c,),Z2(c,)}对应者。

③△1≤0，△2＜0时的情形由图 5示意，因此最优订货周期T*=

图5 情形③

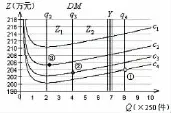
图6 算例中的年总费用曲线

3.2 图解法确定最优订货策略

年总费用函数Z(c,T)的3条性质，为确定最优订货策略打下了基础。但是，由于Z的组合情形有3种，供应商又根据订货批量的不同提供了多个批发价格，加上零售商存在资金约束，具体的情形将变得复杂。在本文假设的情况下，尽管用文字和公式来描述确定最优订货策略的一般步骤是可行的，但将非常繁琐(参见文献[4]中EOQ模型下考虑数量折扣时最优订货策略的确定步骤)。

另一方面，在实际的商业活动中，供应商根据零售商的订货批量设置的批发价格一般不会很多。而且，批量约束和资金约束在Z-Q关系图中都可以简单地表示出来。这使得可以利用具体的参数，通过计算机软件来画出Z(c,T)的函数曲线，并结合约束条件来确定最优订货策略。

供应商是根据订货批量来设置批发价格的，为了作图的方便，利用T=Q/D将Z(c,T)转换为

尽管实际应用中具体的参数各有差异，但用图解法来确定最优订货策略，其步骤是一致的。

步骤1：根据实际情况，设置合适的坐标计量单位。

步骤2：根据延迟支付期M画出DM线。

步骤3：根据式(14)和相关参数，用软件画出各批发价对应的Z(c,Q)曲线，以DM线作为Z1和Z2的分界线。

步骤4：画出各批发价要求的最低订货批量线。

步骤5：将资金约束Y≥cDT-pDM转换为Q≤(Y+pDM)/c，画出资金约束线Y。

步骤6：按照从低价到高价的顺序，在各Z(c,Q)曲线上找出符合约束条件的Z值最小点，然后进行比较，Z值最小的即为最优策略点。在不易分辨时，可以结合△1和△2的值判断Z曲线的构成，必要时可根据公式具体计算。Z值明显都高的曲线可以不参与比较。

4 算例

假设商品需求率D=10000(件/年)；每次订货的订货费S=1000(元)；持有费 h=50(元/年·件)；资金收益利率 I=0.1(1/年)；商品零售价 p=250(元/件)；延迟支付期 M=0.1(年)；零售商在该项商品交易中的投入资金限额Y=100000(元)；商品批发价由下式确定，单位：元。

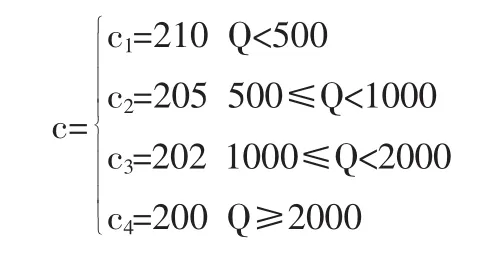
这时△1＞0，△2＞0，即相当于性质 3 中①的情形。

图解法确定最优订货策略的步骤为：首先，结合此算例的实际，将纵坐标Z的计量单位设置为“万元”，横坐标Q的计量单位设置为“×250件”；然后，用软件画出各曲线和约束线(在本算例中DM线和批发价c3的订货批量约束线q3恰好重合)；最后，按照从低价到高价的顺序，在各曲线上寻找关键点，并进行比较。

曲线c4中，点①为符合批量约束的Z值最小点，但不符合资金约束；曲线c3中，点②为符合批量约束的Z值最小点，而且符合资金约束；曲线c2中，点③为既符合批量约束又符合资金约束的Z值最小点，但Z值明显大于点②；曲线c1中所有点的Z值都明显偏高，不予考虑。所以，点②即为最优策略点。此时，

最优订货周期T*=M=0.1(年)

最优订货批量Q*=1000(件)

5 小结

针对供应商给予固定期限的延迟支付期，并根据订货批量的不同设置多个批发价格的情况，假定零售商投入的资金有一固定的最大限额，存在资金约束，本文建立了确定零售商最优订货策略时需要的模型。通过对模型的讨论，在分析年总费用函数特征的基础上，给出了使用图解法来确定最优订货策略的步骤。最后，进行了算例分析。

[1]Goyal S K.Economic Order Quantity under Conditions of Permissible Delay in Payments[J].Journal of the Operational Research Society,1985,36(4).

[2]Das C.A Unified Approach to the Price-break Economic Order Quantity(EOQ)Problem[J].Decision Science,1984,15.

[3]Tersine R J,Toelle R A.Lot Size Determination with Quantity Discounts[J].Production and Inventory Management,1985,27(3).

[4]Goyal S K,Gupta O K.A Simple Approach to the Discount Purchase Problem[J].The Journalofthe OperationalResearch Society,1990,41.

[5]Khouja M,Mehrez A.Optimal Inventory Policy under Different Supplier Credit Policies[J].Journal of Manufacturing Systems,1996,15.

[6]Chung K J,Liao J J.Lot-sizing Decisions under Trade Credit Depending on the Ordering Quantity[J].Computers&Operations Research,2004,31.

[7]Huang Y F.Economic Order Quantity underConditionally Permissible Delay in Payments[J].European Journal of Operational Research,2007,16.

[8]Shinn S W,Hwang H.Optimal Pricing and Ordering Policies for Retailers under Order-size-d ependentDelay in Payments[J].Computers and Operations Research,2003,30.