广义矩方法及其在金融领域的应用

柳会珍，张成虎，周宗泽

(1.西安交通大学 应用经济学博士后流动站，西安 710061；2.西安交通大学 经济与金融学院，西安 710061；3.山西省张峰水库建设管理局，太原 030012)

0 引言

常用的统计估计方法有矩估计法、极大似然估计法、贝叶斯方法和最小二乘法，在这几种方法中，极大似然估计和贝叶斯方法需要总体的概率分布，在实际应用中有较大的局限性而且对模型较为敏感；最小二乘法要求模型的随机误差项和解释变量不相关，因而在处理特殊模型时适用，应用范围较窄。矩估计法是一种简单的统计估计方法，在参数估计中，只需求出和参数有关的矩，并以样本矩代替相应的总体矩，组建一个以参数为未知数的方程组，求解方程组得到参数的矩估计。矩估计不受总体概率分布的限制且不需要实际样本数据的产生过程，因而在实际中得到广泛应用。总体分布中的一个参数可能和多个总体矩有关，由矩估计法对参数进行统计估计就有可能得到多种估计结果，该采用哪种矩估计，这些矩条件之间关系如何协调，哪个矩条件较为重要，这些问题传统的矩估计均无法处理。

本文主要介绍广义矩估计方法的统计思想，对该方法和极大似然估计、最小二乘估计法之间的关系进行了论证研究，同时在数据产生过程具有相关性的条件下对权重矩阵的选取和具体实施过程进行了深入分析，最后给出在金融资产定价方面的应用实例。

1 广义矩方法的统计性质

1.1 统计思想

假设Xt是一个t期观察到的(n×1)随机向量，θ是未知(a×1)参数向量，h(θ，Xt)是(r×1)向量值函数，即 h:Ra×Rn→Rr，满足E(h(θ，Xt))=0，等式中的r行称为正交条件或矩条件。

广义矩方法的统计思想是选取θ使得样本矩g(θ;YT)尽可能接近零总体矩，即广义矩估计θ^使得目标函数Q(θ;YT)=g'(θ;YT)WTg(θ;YT)在θ^达到最小，这里 WT是正定权重矩阵， 根据实际应用中不同矩条件的重要性选取。

取 WT为单位矩阵，则目标函数 Q(θ;YT)=g'(θ;YT)g(θ;YT)，显然 Q(θ;YT)≥0，取θ^使 Q(θ^;YT)=0，即 g(θ^;YT)=0，则θ^是参数 θ的矩估计，所以广义矩估计是矩估计的推广。

1.2 和最小二乘估计以及极大似然估计的关系

考虑多元线性回归模型：

其中Xt=(Xt1，Xt2，…，Xtp)'是t时刻观测到的解释变量向量，β=(β1，β2，…，βp)'是未知参数向量。

在经济和金融领域，常假设解释变量矩阵Xt和随机误差 εt不相关，即 E(Xtεt)=0。 由模型(1)可得这个等式就是广义矩估计法中的正交条件，其中包含p个方程。由于正交条件个数等于待估参数个数p，权重矩阵WT可以取为单位阵，则由广义矩估计的统计方法可知β))的样本矩解得参数向量β的广义矩估计为显然等于普通最小二乘估计，所以普通最小二乘估计是广义矩估计的一个特例。

设Zt是一个t时刻观察到的变量构成的(n×1)随机向量，zt是随机向量 Zt的具体观测值，Zt=(Z1，Z2，…，Zt)表示直到 t时刻所有观察数据。在给定Zt-1的条件下的Zt条件密度为f(zt|Zt-1，θ)，θ是未知参数向量。由密度性质可得：1，A其中表示随机向量Zt的所有可能取值集合。假设微分和积分顺序可交换，两边对参数θ求导得即，令，则有E(h(θ,Zt)|Zt-1)=0，显然正交条件的个数和未知参数个数相同，由广义矩估计法可得：参数θ的广义矩估计满足等式(θ,zt)=0。

将直到T时刻为止观察到的所有样本数据构造似然函数得 L(θ;z1，…，zT)=，对数似然为 lnL(θ；z1，…，zT)=假设函数 f(zt|Zt-1，θ)关于 θ 可微，且最大值在参数空间内部取得，则对数似然函数最大化的一阶条件为显然参数向量θ的极大似然估计和广义矩估计相同，所以在密度函数满足一定的条件下，广义矩估计和极大似然估计是一致的。

1.3 权重矩阵的选取

广义矩估计方法中权重矩阵的选取非常重要，直接决定了正交条件的重要性，即样本矩接近零的关注程度，所以在利用广义矩方法对模型参数进行统计估计时，需要考虑实际问题所需，同时为了后续的模型过度识别检验工作需要，又要照顾到统计分析处理的有效性。

理论上为了保证广义矩估计的渐进有效性，选取的逆矩阵作为权重矩阵，这里是过程的{h(θ0，Xt)}的协方差矩阵，其中 Γi=E(h(θ0，Xt)h'(θ0，Xt))，θ0是参数向量的真实值，这里假设h(θ，Xt)过程是平稳的。

1.4 模型过度识别限制的检验

2 在金融领域的应用

广义矩方法在金融资产定价方面有着重要的应用。Cochrane给出的资产定价公式为：pt=Etmt+1(b)xt+1，其中mt+1(b)是随机折现因子，其中包含了金融资产价格的风险调整因素，b是未知参数向量，xt+1，pt分别是收益向量和价格向量，Et表示已知时刻t时信息下的条件期望[12]。利用期望迭代定律可得：

由于金融资产价格一般变化较大，不具有平稳性，因此为了统计分析处理的方便，我们将公式(2)改写成收益率形式如下：

公式(3)就是广义矩方法中的正交条件。令ut(b)=mt+1(b)Rt+1-1，gT(b)=ET[ut(b)]其中记号ET表示样本均值，则ut(b)是定价误差，gT(b)是定价误差的样本均值。由广义矩方法要求使gT(b)尽可能接近零总体矩，根据不同的金融资产定价误差要求，选取权重矩阵WT，使得Q(b;xT)=gT'(b)WTgT(b)达到最小，求得参数向量b的广义矩估计b^。在金融实证分析中，目标函数Q(b;xT)的最小化可以转化为求参数向量b的广义矩估计，满足等式

等式(4)表示定价误差的线性组合为零，即定价误差向量和一些特殊向量正交，这些特殊向量取决于权重矩阵WT，需要根据实际问题中对各种资产定价误差的关注程度和统计有效性来确定。

由于金融市场的复杂性，金融资产收益率之间存在一定的相关性，而且个别资产收益率变化较大，在选取权重矩阵时均需考虑这些情形，否则得到的广义矩估计不能反映真实的定价误差。

相应的样本均值为

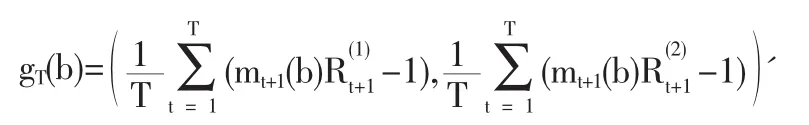
3 总结

由于广义矩估计不需要像传统的极大似然估计和贝叶斯估计那样要求严格的分布假设，更适合复杂的经济和金融系统的参数估计和模型检验，因而近年来在计量经济和金融研究领域得到了广泛的应用，并且随着应用的逐步深入进一步推动了广义矩理论和方法的发展。随着经济发展和金融市场的不断创新，将会出现越来越多的非线性性问题和预测要求，在这些情形下，势必需要最优化、对模型非线性限制的过度识别检验等方法技术，广义矩理论方法能够很好地处理这些模型中的参数估计和检验问题，因而在计量经济学和金融领域将有更广阔的应用前景。

[1]Hansen,L.P.Large Sample Properties of Generalized Method of Moments Estimators[J].Econometrica,1982,50.

[2]Hansen,L.P.,Scott,F.R.The Role of Conditioning Information in Deducing Testable Restrictions Implied by Dynamic Asset Pricing Models[J].Econometrica,1987,55.

[3]Hansen,L.P.,John H.,Erzo,L.Econometric Evaluation of Asset Pricing Models[J].The Review of Financial Studies,1995,8.

[4]Hansen,L.P.,Ravi J.Assessing Specification Errors In Stochastic Discount Factor Models[J].Journal of Finance,1997,52.

[5]Campbell,J.Y.,Lo,A.W.,Mackinlay,A.C.The Econometrics of Financial Markets[M].Princeton:Princeton University Press,1997.

[6]Poon,S.,Rockinger,M,Tawn,J.Extreme-Value Dependence in Financial Markets:Diagnostics[J].Models and Financial Implications.Review of Financial Studies,2003,17(2).

[7]Stock,J.H.,J.H.Wright.GMM with Weak Identification[J].Econometrica,2000,68.

[8]Lars Korsholm.The GMM Estimator Versus Semiparametric Efficient Score Estimator under Conditional Moments Restrictions[C].Working Paper,AarhusSchoolofBusiness,University Aarhus,1999.

[9]詹姆斯D.汉密尔顿,刘明志译.时间序列分析[M].北京：中国社会科学出版社,1999.

[10]Hansen,L.P.Generalized Method of Moments Estimation:A Time Series Perspective[J].InternationalEncyclopedia ofSocial And Behavioral Sciences,2000,6.

[11]Hansen,B.E.,West K.D.Generalized Method of Moments and Macroeconomics[J].Journal of Business and Economic Statistics,2002,20(4).

[12]Jeffrey,C.F.,Giovanny,P.O.Estimating Forward-Looking Euler E-quations with GMM Estimators:An Optimal Instruments Approach[C].Working Paper,Federal Reserve Bank of Boston,2004.

[13]John H.Cochrane.Asset Pricing[M].Princeton:Princeton University Press,2001.

[14]Koenker,R.,Machado,J.A.F.GMM Inference when the Number of Moment Conditions Is Large[J].Journal Of Econometrics,1999,93.

[15]Imbens,G.W.GeneralizedMethod ofMomentsandEmpirical Likelihood[J].Journal of Business and Economic Statistics,2002,20.

[16]Imbens,G.W.,Spady,R.H.,Johnson,P.Information-Theoretic Approaches to Inference in Moment Condition Models[J].Econometric,1998,66.

[17]Brown,B.W.,Newey,W.K.GMM.Efficient Bootstrapping,and Improved Inference[J].Journal of Business and Economic Statistics,2002,20.

[18]Hall,A.R.Generalized Method of Moments[M].New York:Oxford University Press,2005.

[19]Singleton,K.J.Empirical Dynamic Asset Pricing[M].Princeton:Princeton University Press,2006.

[20]Hansen,L.P.Generalized Method of Moments Estimation[C].Working Paper,Department of Economics,University of Chicago,2007.

[21]Newey,W.K.,West,K.D.A Simple,Positive Semi-Definite,Heteroskedasticity and Autocorrelation Consistent Covariance Matrix[J].Econometrica,1987,55.