基于主成分分析的LS-SVM非线形预测模型应用

郭志钢，蒲 忠，李 秋

（1.西南石油大学 经济管理学院，成都 610500；2.中国石油西气东输公司豫鄂管理处，武汉 430073）

0 引言

天然气消费量的预测对于四川省这样的一个天然气资源大省有着非常重要的意义。随着新一轮经济的增长，四川省能源供需矛盾更加紧张，准确的预测不仅关系到四川省能源战略的制定、经济的可持续增长，还关系到人民生活水平的提高。

对于四川省天然气消费量的预测既可以采用时间序列预测方法也可以采用回归预测方法。由于时序预测法只考虑预测对象过去的时序模式，涉及的因素较少，因此建模虽然简单，但是精度有所不够。回归分析方法通常涉及到众多因素，考虑问题比较全面，因此模型尤其是非线形模型相对复杂，但是精度比时间序列模型要高。

本文首先在考虑影响四川省天然气消费量众多影响因素的基础上，选择出比较有代表性的自变量体系，然后为降低预测模型的复杂度以及提高模型的预测精度，利用主成分分析方法对自变量体系进行降维及去噪，把多个自变量变为少数主成分，最后利用这些生成的主成分及应变量（四川省天然气消费量）建立起基于最小二乘支持向量机的非线形预测模型。

1 主成分分析（PCA）

PCA将原样本矩阵分解为一组标准正交基与该正交基所张成的空间中投影坐标的外积，即将过程中大量的相关信息和带有噪声的数据投影到含所有相关信息的低维子空间上，从而起到降维和去噪的作用。计算过程如下：

设 X=(x1，x2，…，xp)T，求 X 的各主成分，等价于求它的协方差矩阵的各特征值及相应的正交单位特征向量λ1≥λ2≥…λp≥0 及 D=(d1，d2，…，dn)。

定义 Y=(Y1，Y2，…，Yn)T为主成分向量，则

即主成分分析是按特征值由大到小所对应的正交单位特征向量为x1，x2，…，xp的线性组合分别为 x的第一、第二、直到第p个主成分，而各主成分的方差等于相应的特征值，即 Var（Yk）=λk。

实际应用中，通常选取m＜p，使前m个主成分的累计贡献率达到较高的比例（如80%到90%）。这样用前m个主成分 Y1，Y2，…，Ym代替原始变量 x1，x2，…，xp不但使变量维数降低，而且也不致于明显损失原始变量中的信息。

2 最小二乘支持向量机（LS-SVM）

基于回归的LS－SVM原理如下：

首先考虑n个训练样本的线性回归问题，设训练数据集(xi，yi)，i=1，2，…，n，xi∈Rd是第 i个样本的输入模式，yi∈R是对应第i个样本的期望输出。线性回归函数为

根据SRM准则，综合考虑正则化项与拟合误差的平方和，将回归问题转化为如下的有约束二次优化问题，它存在唯一的最优解

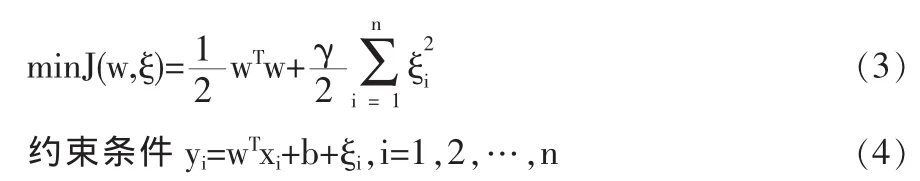
其中γ为可调参数，它控制对超出误差样本的惩罚的程度，实现在训练误差和模型复杂度之间的折衷。与标准SVM不同，这里只有等式约束，且优化目标的损失函数是误差ξi的二范数。引入Lagrange函数，把有约束优化问题转化成无约束优化问题，

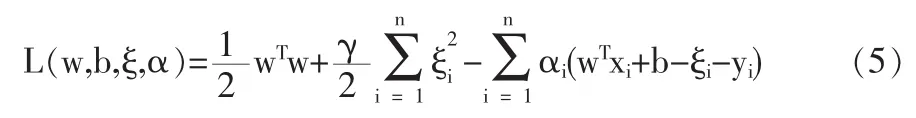
其中 αi≥0,i=1，2，…，n 为 Lagrange 乘子，根据 KKT 条件，把上式对w,b,ξi和αi求偏微分并令它们等于零，得到

上式对于i=1，2，…，n,消去w和ξi得到下面的方程组

解之，得到LS－SVM线性回归模型

由（8）式可以看出，求解LS－SVM线性回归模型的过程只涉及到训练样本之间的内积运算因此在样本维数增加很多的情况下，求解过程的复杂度并没有明显增加，解决了维数灾难问题。对于LS－SVM非线性回归，通常用一个由低维空间到高维空间（Hilbert空间）的非线性映 φ(·):Rd→Rdh，把低维空间的非线性回归转化为高维空间的线性回归，并定义高维空间的内积运算为

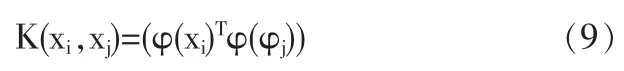
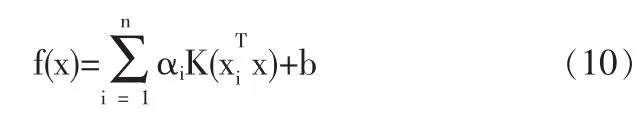
高维空间的内积运算K(xi，xj)称为核函数，它可以是满足Mercer条件的任意对称函数,常用的有多项式核函数、径向基核函数、Sigmoid核函数，本文采用径向基核函数，其公式如下：

其中σ为径向基函数的宽度，为待定系数。

3 实证分析

影响天然气消费量变化因素很多，依据系统性、可行性、科学性的特点，受数据统计的限制，选取四川省工业总产值（亿元）；四川省GDP（亿元）；四川省人均可支配收入（元）；四川省总人口（万人）；四川省固定资产投资（亿元）；四川省天然气产量（亿立方米）；煤炭价格指数（上一年为100%）；电力价格指数（上一年为100%）为自变量体系X，各自变量分别命名为 X1、X2、X3、X4、X5、X6、X7、X8。 具体数据见表 1，其中Y代表四川省天然气消费量（亿立方米）。（数据来源于中国能源统计年鉴及四川省统计年鉴）

3.1 主成分分析

为了达到降维与去噪的目的，首先对样本进行PCA处理。表2为原始样本数据经过标准化处理后的相关矩阵的PCA计算结果。

从表2看出，前两个主成分的累计贡献率已达98.4%，能够很好地概括原始变量。其中，第一个主成分的贡献率为89.5%,并且在所有的变量上都有正的荷载且大小比较平均，因此可以看做是一个综合成分；第二主成分的贡献率为8.9%，在X2上有较大的荷载，因此第二主成分可以看作是工业发展对天然气消费的影响。做主成分与应变量间的散点分析图（图1），从图1可知，主成分与应变量间既存在线形关系，也存在非线形关系，显然使用传统的多元线形回归预测模型来进行预测精度比较低，因此本文采用最小二乘支持向量机这种具有较强非线形拟合能力的机器算法建立预测模型。

表2 X相关矩阵的前两个特征值、特征向量以及贡献率

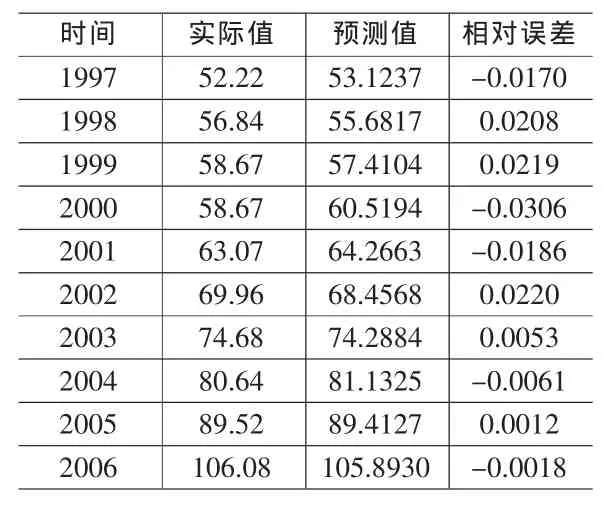
表3 基于主成分分析的LS-SVM模型学习样本及测试样本计算预测结果

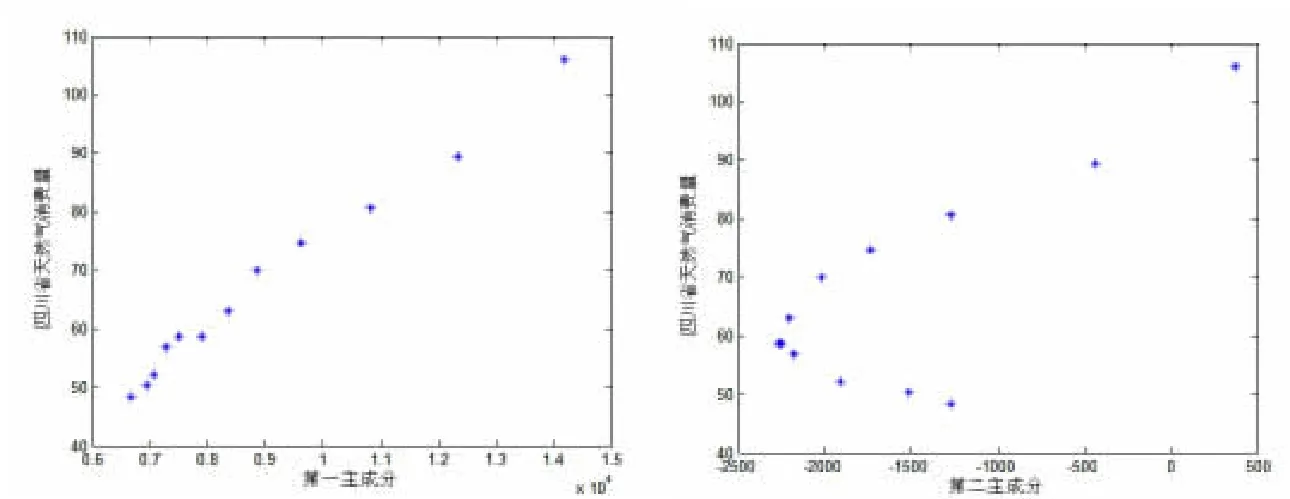
图1 主成分与应变量之间的散点图

表4 三种模型预测性能比较

3.2 最小二乘支持向量机预测模型

以生成的两个主成分作为输入变量，以对应年份的四川省天然气消费量作为输出变量建立LS-SVM预测模型，其中1997年至20005年这九组数据作为学习样本，最后一组数据作为测试样本。

LS-SVM模型的调整参数γ及径向基函数的宽度σ的取值对预测模型的学习及范化能力影响较大，为了提高模型的学习及预测能力，利用遗传算法对最小二乘支持向量机的参数进行优化，优化后的参数取值分别为：γ=5192，σ=21.35。

模型性能结果如表3所示。

为了说明问题，在同样的原始数据的基础上，本文同时建立了基于时间序列的LS-SVM预测模型（模型Ⅱ）及基于主成分分析的线形回归预测模型（模型Ⅲ），并且采用预测样本误差均方差及预测样本相对最大误差两个指标来进行衡量。具体结果见表4，其中模型Ⅰ代表本文所使用的模型。

从表4中可以看出，本文所采用的模型在预测性能指标上远远好于其它两种预测模型，模型Ⅱ虽然通过LS-SVM模型模拟了自变量与应变量间的非线形关系，但是由于模型输入变量包含的信息相对较少，因此预测误差相对较大。模型Ⅲ虽然包含较广自变量信息，但是由于仅使用线形回归进行分析，显然不符合自变量与应变量间的非线形关系，因此误差比较大。而本文所建立的模型综合上述二者的优点，模型自变量包含的信息较多，预测时丢失的信息较少，同时经过主成分分析实现了降维及去噪；另一方面利用LS-SVM模型成功的模拟了自变量与应变量间所存在的非线形关系，因此预测性能要远强其它两外两种模型。

4 结论

本文使用主成分分析方法对影响四川省天然气消费量影响因素进行降维及去噪，利用遗传算法改造后的最小二乘支持向量机回归方法建立四川省天然气消费量预测模型。结果表明该模型具有较强的学习能力及范化能力，具有一定的应用价值。

[1]郭志钢.四川省天然气消费量变权重组合预测[J].西南石油大学学报(社会科学版)，2009.2.（2）.

[2]王革丽.基于支持向量机方法对非平稳时间序列的预测[J].物理学报，2008,(2).

[3]周辉仁.LS-SVM的参数优选及铁路客运市场预测[J].计算机工程与应用，2007,43（30）.

[4]王效东.天然气消费量的神经网络方法预测[J].天然气勘探与开发，2007,(9).

[5]覃章健.四川省成品油和天然气需求预测[J].资源科学，2006,(9).

[6]殷建成.天然气需求自适应优化组合预测模型的改进[J].油气储运，2005,24（10）.

[7]永高,孙文建.基于主成分分析法的建筑企业竞争力评价研究[J].施工技术，2007,（12）.

[8]万玺.重庆市“十一五”天然气需求组合预测研究[J].天然气技术，2007,(6).

[9]Pelckmans K，Suykens Jak，DE Moor B.Building Sparse Representations and Structure Determination on LS-SVM Substrates[J].Neurocomputing,2005,(64).