Spreadsheet在集货型运输车辆调度优化中的运用
2010-04-23上海东海职业技术学院上海200241
高 振(上海东海职业技术学院,上海 200241)
0 引 言
车辆调度优化(Vehicle Schedule Problem,VSP)是物流研究领域中的热点和难点,也是影响物流运输成本的最重要的问题,该问题的一般描述是:对一系列装货点(或卸货点),组织适当的行车路线,使车辆有序地通过它们,在满足一定的约束条件(如货物发送量,车辆载重限制,车厢容积限制,时间限制等)下,达到一定的目标(如路程最短,费用最少,时间尽量少,适用车辆数尽量少等)。从不同的角度该问题可以归为不同的类型,从车辆运输任务的性质分为纯装货问题(也称为集货型)、纯卸货问题,以及装卸混合问题,从优化的目标分为单目标与多目标,目标的性质可以是运输成本最低、运输路程最短、车辆空载率最低、所需车辆数最少、服务准确性最高等,从车辆类型不同分为单车型与多车型,从时间限制上可以分为有时间约束和无时间约束的优化问题,等等。例如,已知单车场、单车型、无容量限制的车辆在无方向运输网络的取货点收集单位需求量,只考虑运输费用最小遍历路线的总长度的目标函数,该问题就是“旅行商问题”。本文所要讨论的是运输成本最小单一目标优化、多车型、集货型,不考虑时间约束的车辆调度优化。
Spreadsheet方法是近年来美国各个大学乃至企业推广的一种管理科学与应用的有效方法,现也在我国的理论研究与企业实践中广泛使用,其在EXCEL或其他背景下将所需要解决的问题进行描述与展开,然后建立数学模型,并使用EXCEL的命令与功能进行预测、决策、模拟、优化等运算与分析。车辆调度优化在物流实践中的普遍存在,其直接决定了物流运输成本的高低,正因为在实践中如此普遍,也才成为理论研究的热点,大家都从不同的角度来研究该问题,希望能在实践中提高决策效率、降低物流成本。但理论上提供解决车辆调度优化的方法与实际应用还存在一定的距离,比如理论研究中常用来求解该问题的方法有遗传算法、退火算法等,不容易被企业管理人员所掌握。Spreadsheet方法是在EXCEL背景下运行,大多数企业管理人员都能掌握。本文运用Spreadsheet方法解决集货型物流中心车辆调度优化问题,即从单一物流中心派出运输车辆到不同取货点取货,然后返回物流中心,满足一定的运输约束,达到运输成本最小的目标。
1 问题的提出
已知某物流中心需按国外客户要求其从25个不同供应商的工厂取货,然后集中在物流中心,分类装入集装箱再装船出口。由于远洋集装箱船舶是周班,因此对物流中心来说,车辆调度优化的工作周期也是一周。
物流中心与每一个取货点之间的运输称为一条“线路”,设有M条线路Ai,i=1,2,3,…,m,尽管有多达25个不同的取货点,但是这些取货点可以按照地理区域分为5个大的组团,这样就可以简化处理为m=5。
每个取货点每次准备发运的货物数量分别为Vi,i=1,2,3,…,m,即把每一个组团内所有不同取货点的货运量相加,得到Vi,i=1,2,3,4,5。
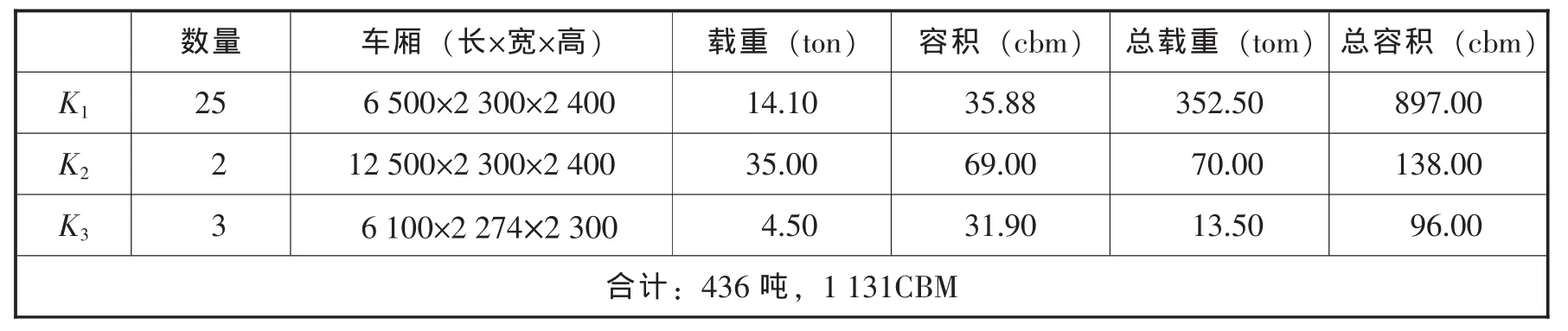
表1 物流中心车辆运力表
物流中心有n种不同型号的卡车Kj,j=1,2,3,…,n,每种型号卡车的数量分别用kj表示,由上可知,j最大为3,即k1=25,k2=2,k3=3。
每种不同型号车辆在不同线路上的单位运输成本记为Cij,当i=3,j=2,即C32表示第二种型号的卡车在第三条线路上的单位运输成本。
用Xij表示在第i条线路上由第j种车辆装载的货运量(立方米)。
目标是:在车辆运力限制条件下,如何分配不同数量的车辆在不同线路上运行,达到运输成本最小。

表2 不同线路不同车辆运输成本表
2 分析及建立模型
以上案例的目标是实现运输成本最小,将不同类型的车辆分派到不同的取货点取货,然后返回,即在各车型在各条线路运输成本一定的情况下,多少数量的什么车型到哪个取货点去取货,才能达到运输成本最小的优化问题。本案例与运筹学中的“运输问题”实质上是一个类型,“运输问题”是决定将不同产地的产品(产量)分派到需要产品的不同销地(销量),使成本最小或利润最大,本案例是将车辆的运力(产量)分派到需要运力的取货点(销量),达到运输成本最小。
现选取某一周的运量数据为例,如表1~3,运用Spreadsheet方法求解。
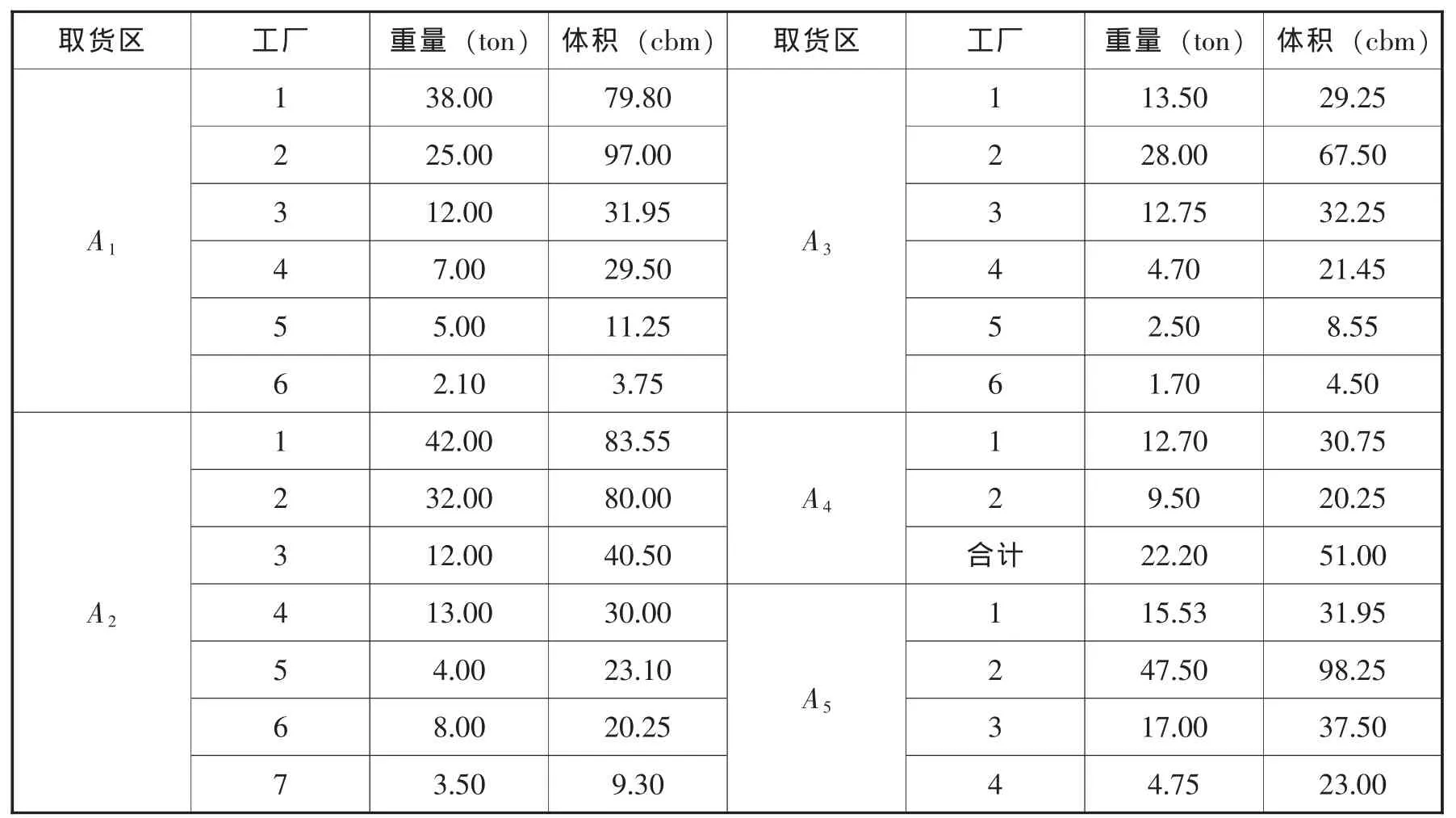
表3 物流中心某一周货运量数据
为使计算简化,我们将物流中心车辆运力(以车厢容积计),按一定的比例折算后与货运量保持一致,也就是说尽量构造成运输问题的标准形式,即“产销平衡”。案例中的折算比例为83%(945/1 131=0.83)。该折算比例的实际意义是:按优化后的车辆车厢容积的利用率如果达到83%,就认为按该优化的方案达到了最理想的效果,如表4所示。

表4 折算后的车辆运力与货运量平衡表
因此优化模型可以写成:
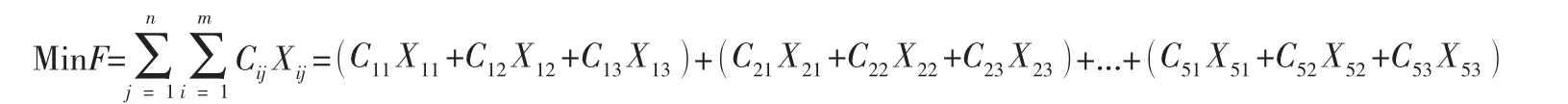
约束条件:
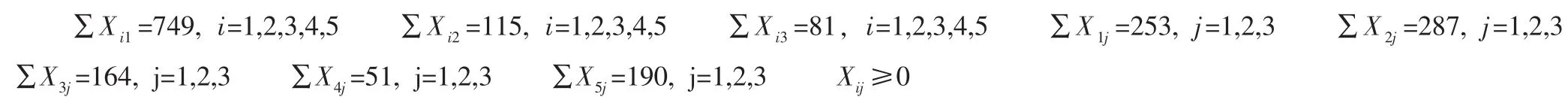
根据以上模型,可以得到每条线路上,具体每种车型需要承担的运输货运量,再将货运量数据除以相应的车辆类型的车厢容积,就可以求出在每条线路上的车辆分配情况。
3 应用Spreadsheet方法求解
第一步:输入已知数据:
在EXCEL表格的$C$6:$G$8区域输入各种车型在不同线路上的单位运输成本。
第二步:输入决策变量,目标函数,约束条件:
(1)决策变量:在$C$13:$G$15,$C$20:$G$22为决策变量的输出区域,在C20单元格输入=C13/36,并拷贝D20,E20,F20,G20;在C21单元格输入=C14/69,并拷贝 D21,E21,F21,G21;在 C22单元格输入=C15/32,并拷贝 D22,E22,F22,G22。
(2)目标函数:在J9单元格输入公式::=SUMPRODUCT(C6:G8,C13:G15)。
(3)约束条件:在C16单元格输入=SUM(C13:C15),拷贝到D16,E16,F16,G16,在 H13单元格输入=SUM(C13:G13),拷贝到 H14,H15。
(4)求解:打开EXCEL页面菜单“工具”中的“规划求解”命令,在参数框中输入目标单元格J9(目标函数地址),在可变单元格输入$C$13:$G$15(决策变量地址),在约束单元格输入:$C$16:$G$16=$C$17:$G$17,$H$13:$H$15=$J$13:$J$15,$C$13:$G$15≥0。
完成以上步骤后,在规划求解参数框中单击“求解”,即能达到本案例的最优解,如图1所示。最优解为:A1线路分派4(3.8入位取整)辆K1车和2(1.7入位取整)辆K2车,A2线路分派8辆K1车,A3线路分派5辆K1车,A4线路分派2辆K1线路,A5线路分派3辆K1车和3辆K3车,共有22辆K1,2辆K2,3辆K3被分派,最小运输成本是96 264。
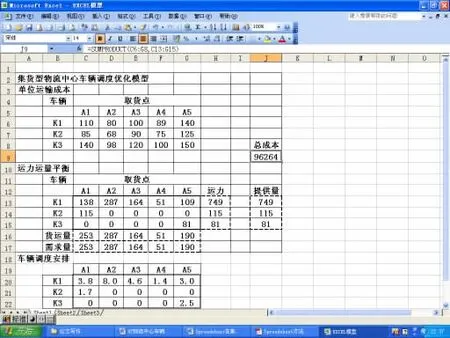
图1
4 结束语
将车辆运力调度问题构造成“运输问题”的产销平衡的标准形式,采用Spreadsheet方法建模和求解,对集货型运输车辆调度问题进行了讨论,取得了较好的结果,达到降低成本的目标,尤其是为物流企业管理人员提供了一种实用且简便的决策方法。
[1]李军,郭耀煌.物流配送车辆优化调度理论与方法[M].北京:中国物资出版社,2001.
[2]丁以中,Jennifer Shang.管理科学-运用Spreadsheet建模和求解[M].北京:清华大学出版社,2003.
[3]郎茂祥.配送车辆优化调度模型与算法[M].北京:电子工业出版社,2009.
[4]丁以中.在管理科学教学中运用Spreadsheet教学法的探讨[J].上海海事大学学报,2001,23(1):76-81.
[5]杨神化,关克平.Spreadsheet方法在港口吞吐量预测中的运用[J].武汉理工大学学报:交通科学与工程版,2005,29(5):801-804.
