双配送中心选址方法

鲁晓雪，李 菲，丛 茗，张 燕，胡贤满

（北京物资学院，北京 110011114499）

0 引 言

配送中心，作为物流网络的节点，对其选择的合理性不仅影响到配送中心本身的运营成本、运营绩效、竞争战略和未来的发展，而且还影响到配送中心上游的供应商、下游的分销商或零售商的物流成本，以及物流战略和竞争战略，甚至影响到区域经济的发展。因此，对于配送中心选址的问题要进行综合考虑，以达到高效、低成本满足各方要求[1]。

物流配送中心选址方法可分为三类，包括应用连续型模型选择地点、应用离散型模型选择地点和应用德尔菲（Delphi）专家咨询法选择地点。应用连续型模型选择地点在实际中很多条件都是无法实施的，而应用离散型模型选择地点不仅所需的基础资料多，而且计算工作量也是相当大的。这两种方法都是不易在实际中应用的。因此，本文选择应用德尔菲（Delphi）专家咨询法，在综合考虑各方因素的前提下，结合重心法、层次分析及Delphi法，提出了一种简单的选址方法。在各类文献中，多是对单中心的选址问题的解决方法，但是在实际工作中，存在很多配送中心选址的问题，即以多个地点为配送中心的问题。本文仅考虑其中的双配送中心选址问题，并给出相应的配送中心选址算法。

实际工作中，当所需配送货物处于一个较大的区域内并且要配送到多个地点时，往往一个配送中心是不能满足所需的。若某个地点距离配送中心较远时，那么所花的时间及运费就是相当高的，这大大影响了企业的利益。为此，可以在一个较大的区域内选择两个或两个以上的配送中心来满足所有地点需求。

本文考虑双配送中心选址问题，即在一个较大的区域内选择两个地点建立配送中心。假设某区域内有n个需求点，已知每个需求点所需的货物量、价值权重及每个需求点在坐标平面上的位置、城市距离系数等，如何在满足各种自然、社会、政治等因素的前提下，选出的两个配送中心地点，使所选配送中心满足各个需求点的需求，并且使企业效益达到最大化。

1 算法描述

1.1 初始选址

1.1.1 划分出两个区域

根据聚类算法的思想，即同一类对象的相似度较高，而不同类的对象相似度较小的原理，将需求点划分成两个区域。在本文中，相似度的度量主要使用欧氏距离，首先计算所有需求点间的距离并以距离为边权构造一个完全图，然后，在该图中，将最大距离对应的两个需求点之间的边删除，再对余下的图选择最大距离的边删减，依次进行下去，直到图被划分成两个不连通的部分图为止，这两个不连通的图恰好对应两个区域。

1.1.2 利用重心法初始选址[2]

在整个物流系统中，将各个地点对货物的需货量及供应量看做物体的重量，利用求物体系统重心的方法来确定物流网点的位置，将求得的位置作为配送中心的最佳设置点，也就是初始选址地点。

其中，X,Y分别为所确定的重心的横纵坐标；Xi,Yi分别为各个地点的横纵坐标；wi表示所需货物重量的权重，即每个需求地的货物量；hi表示城市距离系数，因各个地点的距离并不能用直线表示，因此两地的直线距离与城市距离系数的积才是实际的距离。

1.2 进行筛选，确定最终选址地点

1.2.1 确定筛选地址的指标[3]

由于影响选址的因素很多，例如自然条件、经济因素、社会因素、政治因素等，因此要全面考虑各种因素对选址的影响。本文将货运总量大小、社会固定资产投资、社会消费品零售总额等作为影响筛选地址的评价指标，并根据各指标建立层次模型，包括目标层、准则层及方案层。

1.2.2 建立成对比较矩阵[4]

根据所建立的层次模型，建立成对比较矩阵。通过成对比较矩阵及1～9判断尺度来表示两个指标间的相对影响程度。再通过计算得出权重向量及进行一致性检验。

1.2.3 利用DELPHI法评分

邀请相关专家对各个筛选后的地点依据所构建的评价指标进行评价，将评价结果分为特优、优、良、中、差五个等级。

1.2.4 根据模糊综合评价方法确定隶属度[5]

根据评价函数，计算出属于各等级的隶属度，进而确定最佳配送中心地点。

2 实例应用

本文选取文献[3]中的朝阳柴油机厂配送中心选址问题的数据进行应用计算。朝阳柴油机厂的供应商遍布全国各地，其供货时间和数量相对比较随机，但由于一些地点的供货都是小批量的，因而无法形成规模效应，这就使得朝柴厂在运输方面也需要大量的投资。在这种情况下，选择一个配送中心作为自己供货的暂存区以应对长期发展就显得尤为重要。因为朝阳柴油机厂供应商以长三角地区的居多，所以配送中心的选择以长三角地区为主。

表1为朝阳柴油机厂的主要需求者的需货量、城市距离系数及城市坐标等信息。

2.1 初始选址

根据所提出的算法，将所有区域划分为两部分A和B，如表2、表3。并且利用离散重心法求出所划分后的区域内的备选地点。其中，价值重量表示需货量wi，价值重量=需求货物重量×价值权重。

根据计算得出初步选址点（148.196,67.056）根据此点，通过对横纵坐标的综合考虑，选出A区域内的备选地点为南京，芜湖，仪征。

根据计算得出初步选址点（164.871,52.378）根据此点，通过对横纵坐标的综合考虑，选出B区域内的备选地点为苏州，湖州，余姚。

2.2 进行筛选，确定最终选址地点

2.2.1 确定筛选地址的指标

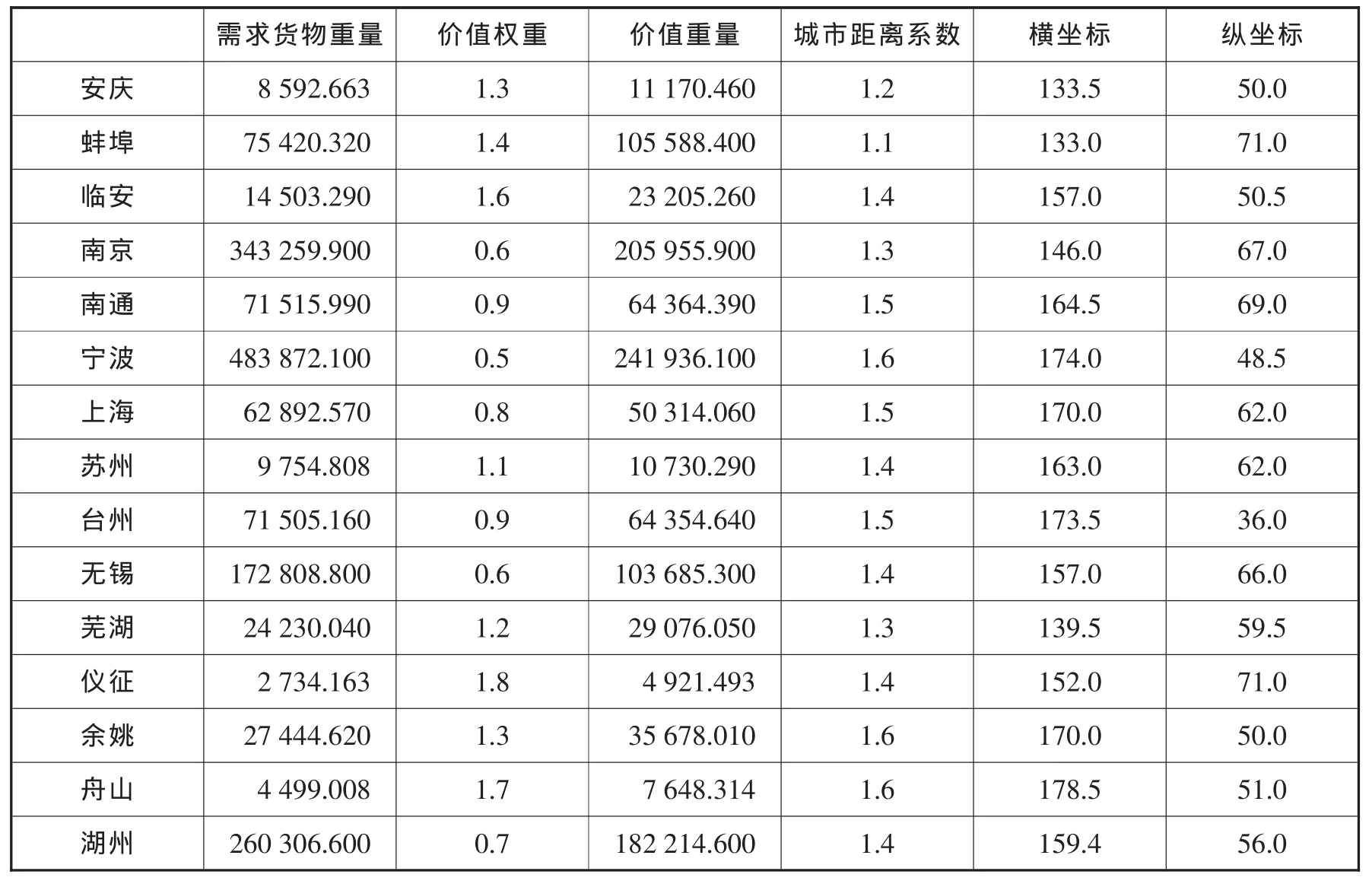
表1

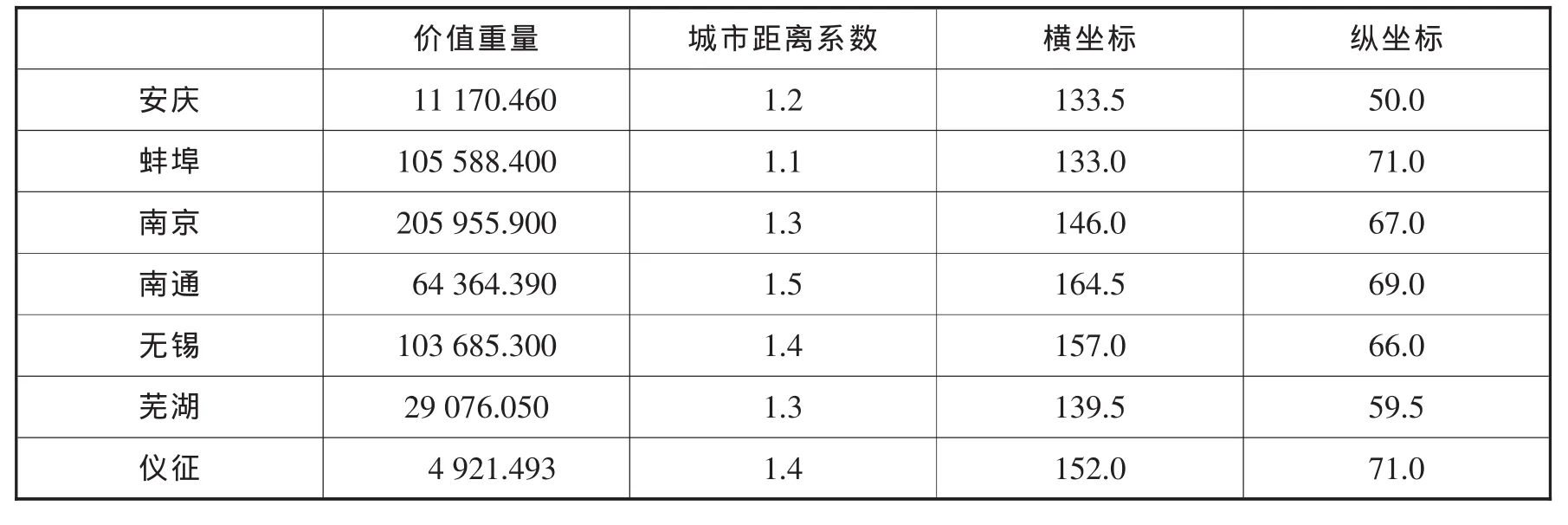
表2

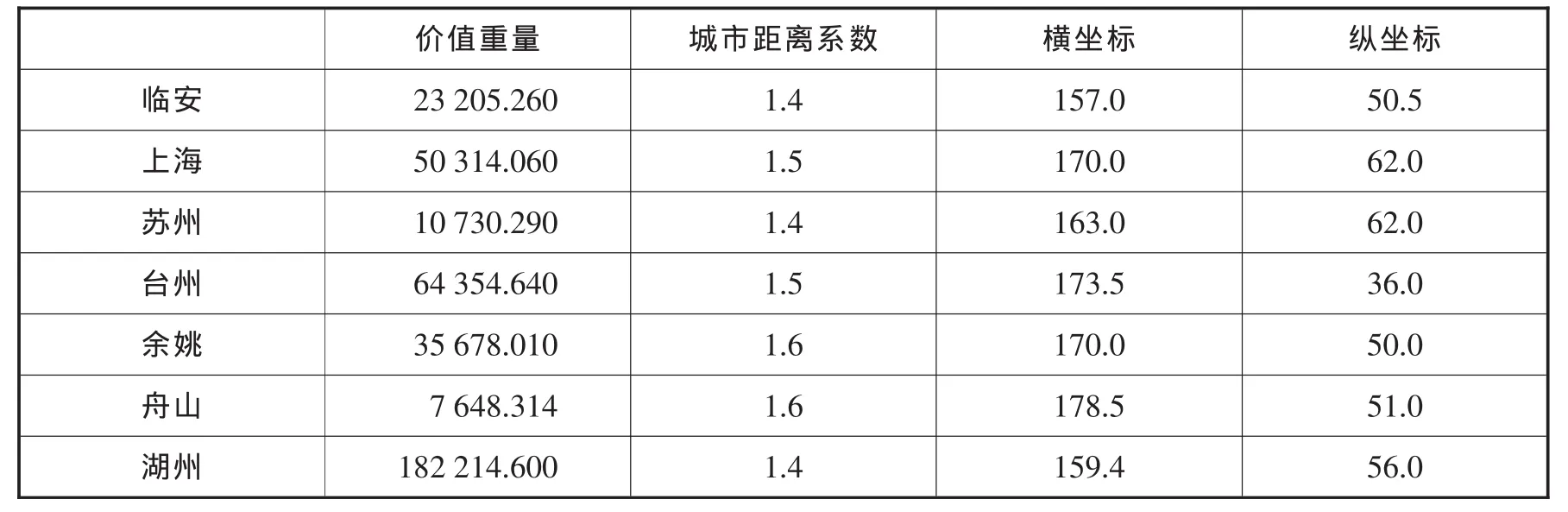
表3

建设配送中心，不仅要考虑其规模及对其的投资，也要考虑其对企业发展的影响。因此选择配送中心地址要充分考虑各种因素，比如政府对城市的优惠政策、配送中心的经营成本、地点交通的便利性等等，当然要以实现利益最大化及费用最低化为目标。因此，提出10个准则层，对城市进行评价，即货运总量大小、社会固定资产投资、社会消费品零售总额、交通便利性、土地价格、人力资源、物流业发展情况、税收水平、支持力度、城市定位。根据这些因素建立层次结构模型，如图1。

2.2.2 建立成对比较矩阵

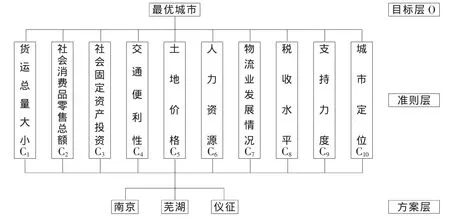
图1

根据一致性检验计算方法，得出CR=0.0074＜0.1，所以满足一致性检验。

2.2.3 DELPHI法评分

以区域A里的南京为例。制订评分标准为特优、优、良、中、差，在通过某高校物流专业教授、某物流公司管理层和相关企业咨询专家共10人一句各种指标对其进行评分后，得出如下结果，见表4。

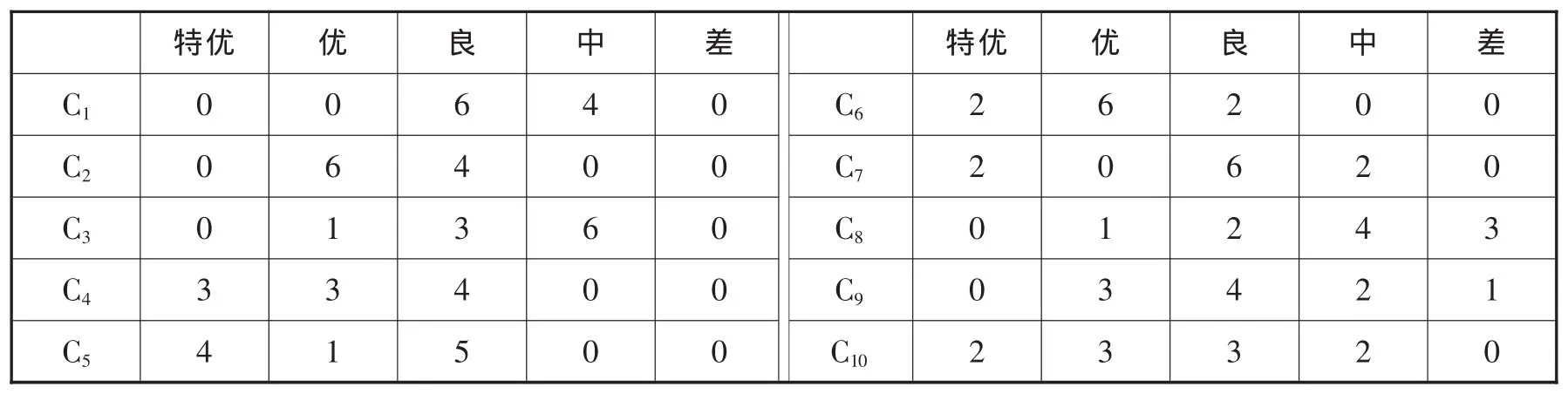
表4

2.2.4 根据模糊综合评价方法确定隶属度

根据评价函数，可知隶属度矩阵如下：

最后得出南京的隶属度b1=r×w= [ 0.288 0.179 0.421 0.018 0.094]。可知南京属于“优”的隶属度最大为0.421，按照同样的算法，可得出A区域内芜湖和仪征的隶属度，分别为：

b2= [ 0.1248 0.2767 0.3658 0.2243 0.0064]b3= [ 0.1371 0.2485 0.3458 0.2388 0.0278]即芜湖属于“良”的隶属度b2最大为0.3532，仪征属于“良”的隶属度b3最大为0.3458。因此，经过选择，南京为最佳的配送中心选址地点。

在B区域内，可用同样的方法计算得各地点的隶属度，并选择最佳配送中心选址地点。各个地区隶属度分别为：

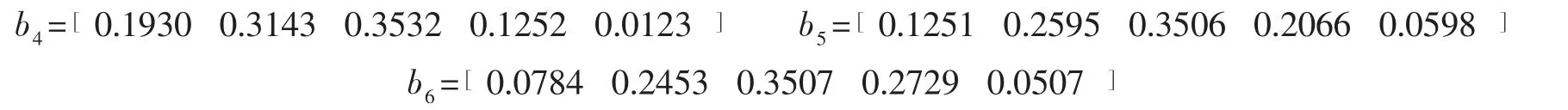
即苏州属于“良”的隶属度最大为0.3532，湖州属于“良”的隶属度最大为0.3506，余姚属于“良”的隶属度最大为0.3507。三个地点的隶属度值十分接近，但经过调查，苏州成为重点建设城市之一，因此，苏州为最佳的配送中心选址地点。

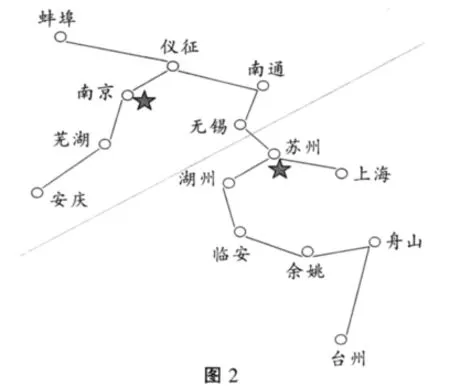
通过图2可以看出，南京、江苏为最佳的配送中心选址地点。

苏州是交通部授予的公路交通枢纽城市，座落于长江三角洲地区的地理中心，位于长江南岸的入海口处，京杭大运河、京沪铁路和多条高速公路贯穿全境，而苏州内的苏州港作为长江三角洲地区的集装箱干线港，成为了上海国际航运中心集装箱枢纽港的重要组成部分、江苏第一大外贸港，为长江沿线外向型经济发展和以集装箱为主的外贸物资运输提供服务。

南京是长江三角洲内第二大城市，位处长江下游，京沪铁路、宁芜铁路、宁西铁路等铁路交汇于南京，使南京成为连接华北、华东和华中的重要铁路交通枢纽。南京现有的南京长江大桥、南京长江二桥、南京长江三桥三座跨江大桥更好地推进跨江发展，而南京港作为仅次于苏州港、南通港的中国第三大内河航运港，长江沿岸仅次于上海外高桥和苏州港的第三大集装箱港，促进了区域的统筹发展。

综上所述，通过苏州及南京良好的交通运输网络以及其对经济发展的需求，说明配送中心选在这两个地点是合理的。

3 结束语

本文结合实际问题，即双配送中心的选址问题，在考虑了影响选址的各种因素，如：地理、地形、地物、地基、环境、交通、劳动力、城市用地、城市发展等等后，应用重心法、选址评价指标体系和应用模糊评价，层次分析等数学方法进行综合评价，进而确定出物流配送中心的最优位置，所得出的结果是科学、合理的。虽然在选取评价指标及确定专家评分时会有一些人为因素干扰，但如果严格按照约定进行，这些因素的影响是可以减少或消除的。

注：本文中所有数据结果均由MATLAB程序计算得出。

[1]蔡临宁.物流系统规划——建模及实例分析[M].北京：机械工业出版社，2008:1-50.

[2]王非，徐渝，李毅学.离散设施选址问题研究综述[J].运筹与管理，2006(10):64-69.

[3]孙焰，郑文家.基于重心模型和层次分析法的配送中心选址研究[J].物流科技，2009(3):33-35.

[4]陈东彦，李冬梅，王树忠.数学建模[M].北京：科学出版社，2007:195-212.

[5]范丽芳，江浩斌，陈昆山.基于模糊层次分析的配送中心研究[J].交通运输系统工程与信息，2006(2):107-110.