EMD-EKF方法研究

（海军航空工程学院 电子信息工程系，山东 烟台 264001）

0 引言

扩展卡尔曼滤波（EKF）是在工程实践中应用较为广泛的滤波方法。该方法利用泰勒级数展开，将非线性滤波问题转化为线性滤波问题。但是，EKF滤波在进行滤波前假定过程噪声和量测噪声为互不相关零均值白噪声，且噪声的统计特性是已知的。噪声的不准确将会导致EKF方法给出的均方误差偏离真实情况，有时不能准确反映状态估计精度。因此，在先验信息不完全的情况下，采用与真实值相差较多的观测噪声标准差进行EKF 滤波，得到的状态滤波方差有时无法反映状态滤波精度，状态滤波结果并不总是可靠的。同时在实际应用中，动态系统随时可能受到各种外界干扰，因此观测噪声的统计特性随时会发生变化，仅仅依靠有限的先验信息对观测噪声进行描述是不可靠的，需要一种能够对观测噪声进行实时估计的方法[1-3]。

1 EMD方法

经验模态分解方法（EMD）从本质上讲是对一个信号（或其导数，视所需的分解精度而定）进行平稳化处理，其结果是将信号中不同尺度的波动或趋势逐级分解开来，产生一系列具有不同特征尺度的数据序列，每一个序列被称为一个本征模态函数（Intrinsic Mode Function，IMF）。最低频率的IMF分量通常情况下代表原始信号的趋势或均值。作为一种运用，EMD方法可以有效地提取一个数据序列的趋势或去掉该数据序列的均值。测试结果表明，EMD方法是目前提取数据序列趋势或均值的最好方法[4]，EMD方法的另一目的是为了进一步对各IMF分量进行Hilbert变换，获得信号的瞬时频率。

通过对信号进行平稳化处理，可以分解出n个IMF分量ci(t)和趋势项rn(t)。即

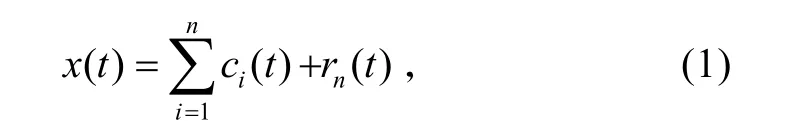
式中，每个IMF分量都是平稳信号。

EMD方法（平稳化过程）基本思想是：假如一个原始信号序列的极大值或极小值数目比上跨零点（或下跨零点）的数目多出两个（或两个以上），则该数据就需要进行平稳化处理。具体方法是：找出原始数据序列的所有极大值点并将其用样条插值函数插值成为原始数据序列的上包络线；找出原始数据序列的所有极小值点并用样条插值函数插值成为原始数据序列的下包络线；上、下包络线的均值为原始数据序列的平均包络线；将原始数据序列减去该平均包络后即可得到一个去掉高频的新数据序列。

在频域上，信号经EMD 分解的各个IMF的瞬时频率之间有如下关系：第1个IMF 含最高瞬时频率成份，第i（其中i≥2）个IMF的瞬时频率几乎处处是第i+1个IMF的瞬时频率的两倍[4]。因此，信号经EMD 分解出的各个IMF可以看做是对原信号进行带通滤波的结果[4-8]。通过EMD方法可实现时空尺度滤波，即对一个能分解出n个IMF的信号其低通滤波为：

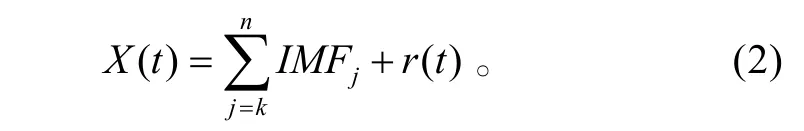
由于噪声频率一般较高，而各个IMF的频率几乎是按2的负幂次方的形式递减[5]，所以各个IMF所包含的噪声其强度也越来越弱。因此，低频IMF几乎就是期望信号的低频分量。

2 EMD-EKF方法

考虑如下非线性模型

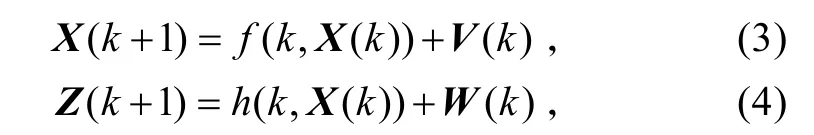
式中：假定过程噪声和量测噪声均为加性零均值白噪声。

扩展卡尔曼滤波的方法一般流程如下[1-3，9-10]：

预测：

状态的一步预测

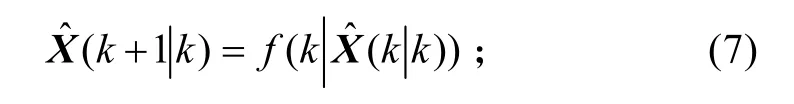
协方差的一步预测

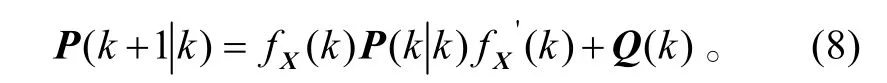
更新：

量测预测值

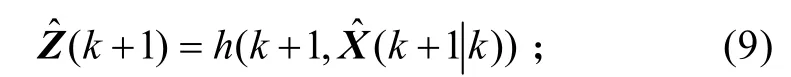
协方差

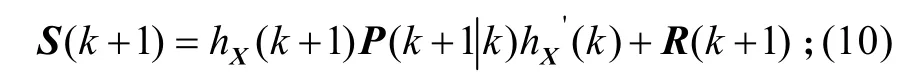
增益

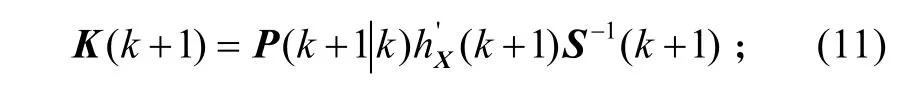
状态更新方程

协方差更新方程

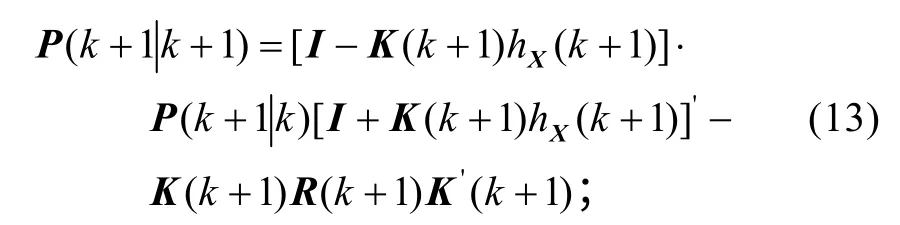
其中，I为与协方差同维的单位矩阵。

经验模态分解方法具体步骤如下[7-8，11-12]：

1）计算出原始信号Z(t) 所有的极值点。

2）采用三次样条插值算法，求解所有的极大值点构成的上包络线和所有的极小值点构成的下包络线，分别记为u1(t)和 v1(t)；在这一步骤的计算中，为了抑制边缘效应，需使用镜像延拓的方法来延拓极值点。

3）记上、下包络线的均值为：

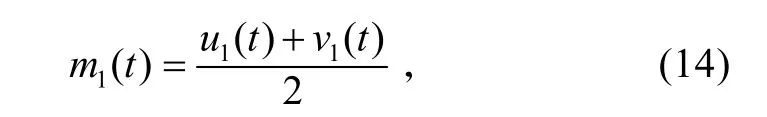
并记信号与上、下包络线的均值之差为：

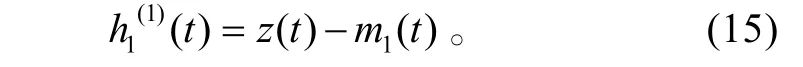
4）判断 h1(1)(t)是否满足IMF的两条性质。若满足，则 h1(1)(t)为IMF。否则，记 h1(1)(t)为Z (t)，重复步骤1）至步骤4），假定k次筛选后得到的h1(1)(t)满足IMF定义，则Z (t)的第一阶IMF分量c1(t)=h1(1)(t)。

5）记 Z1(t)=Z(t) − c1(t)为新的待分析信号。重复步骤1）至步骤5），以得到第二个IMF，记为c2(t)，余项 Z2(t)=Z1(t) −c2(t)。

重复上述步骤，直至满足停止条件，分解结束。如此，可得到余项Zm(t)。

经验模态分解方法能够分离信号和噪声，因此可以用来估计含噪声信号中噪声的标准差。在观测噪声未知的情况下，可以首先选取一段长度为L的一段信号，即相当于一个观测区间，在这个观测区间上进行经验模态分解，分离出其中的高频噪声，估算出观测噪声的标准差。根据这个标准差结合EMD 滤波，进行状态估计。

本文的方法与常用的EKF方法的主要区别在于量测噪声协方差矩阵不是预先根据经验值确定的，而是根据实时观测信号值估计出来的。这就保证了计算用的量测噪声协方差矩阵和实际系统观测噪声协方差基本一致，即使实际系统由于受到某种干扰，噪声协方差发生了变化，该方法也能计算出量测噪声的参数。

3 仿真结果

无源定位是EKF 滤波的一个重要应用领域，下面就单站无源定位中的跟踪定位问题进行仿真。

在实际的系统中，各个观测量随时都有可能受到各种外界干扰，导致观测噪声发生变化，假定运动单站通过方位角进行无源定位，观测时间间隔T=2s，连续观测100 s。传感器初始位置为(−5 000,0)，在y轴上做匀速直线运动v=4m/s，在x轴和y轴方向上的扰动 rx=0.1、r y=0.1。目标初始位置为(0,0)，在y轴上做匀速直线运动v=3m/s，系统噪声Q=16。定义相对位置误差（Relative Position Error，RPE）来描述方法的性能：

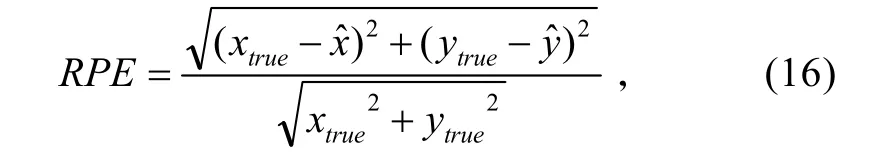
式中：(xtrue,ytrue)为真实相对位置；(x,y)为相对位置的估计值。

图1是在变噪声条件下进行了仿真，观测噪声在0～50 s为3 mrad，在50～100 s为5 mrad，图1共对两种情况进行了仿真。情况一为本文方法，即首先用EMD 估计量测噪声协方差，再进行EKF 滤波，情况二为采用通过先验信息确定的量测噪声方差进行EKF 滤波。

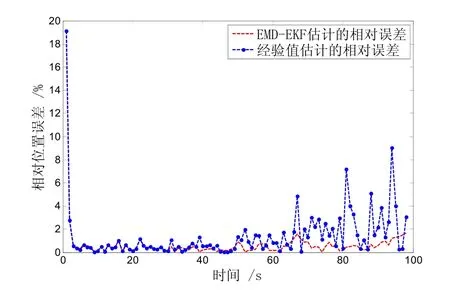
图1 量测噪声为0～50 s为3 mrad，50～100 s为5 mrad

从图1和表1中可以看出本文方法的滤波效果明显好于使用经验值的方法，这是因为采用EMD方法可以实时确定量测噪声方差，因此在此基础上进行的滤波效果更好。其中，进行200次蒙特卡罗仿真，使用本文方法耗时15.64 s，使用经验值方法耗时1.34 s。

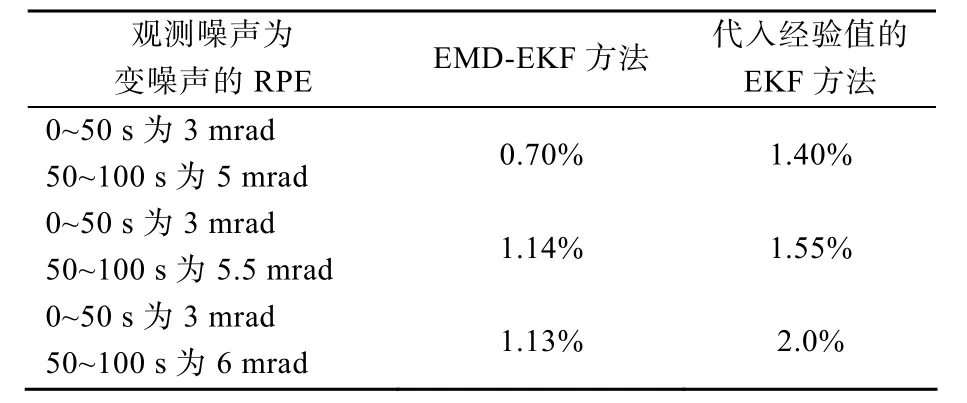
表1 EMD-EKF方法和EKF方法平均相对误差的比较

4 结束语

不准确的量测噪声方差统计特性往往会导致EKF 滤波性能恶化。本文针对这一问题，采用EMD方法实时估计观测噪声序列的噪声标准差，并利用估计量测噪声序列的噪声标准差进行EKF 滤波。仿真结果表明，本文方法可以实现测量量测序列噪声的变化，准确估计出量测噪声标准差，从而避免了因量测噪声的不准确而引起的EKF 性能下降。

[1]何友,修建娟,张晶炜,等.雷达数据处理及应用[M].北京:电子工业出版社,2008:42-46.

[2]PEARSON J B,STEAR E B.Kalman filter applications in airborne radar tracking[J].IEEE Transactions on Aerospace and Electronic systems,1972(10):319-329.

[3]JOSEPH J,LAVILOLA JR.A comparison of unscented and extended kalman filtering for estimating quaternion motion[C]//The proceeding of the 2003 American Control Conference.2003:2435-2440.

[4]邓拥军,王伟,钱成春,等.EMD方法及Hilbert变换中边界问题的处理[J].科学通报,2001,46(3):257-263.

[5]PATRICK FLANDRIN,GABRIEL BILLING,PAULO GONCALVES.Empirical mode decomposition as a filter bank[J].IEEE Signal Processing Letters,2004,11(2):112-114.

[6]陈克安,马远良.自适应有源噪声控制——原理、算法及实现[M].西安:西北工业大学出版社,1993:133-140.

[7]杨世锡,胡劲松,吴昭同,等.旋转机械振动信号基于EMD的希尔伯特变换和小波变换时频分析比较[J].中国电机工程学报,2003,23(6):119-121.

[8]谭善文,秦树人,汤宝平.Hilbert-Huang变换的滤波特性及其应用[J].重庆大学学报,2004,27(2):9-12.

[9]管旭军,芮国胜.基于UKF的单站无源定位算法[J].电光与控制,2004,11(1):34-36.

[10]芮国胜,管旭军.一种机动目标无源定位的新方法[J].宇航学报,2005,26（增刊）:121-125.

[11]刘慧婷,张旻,程家兴.基于多项式拟合算法的EMD端点问题的处理[J].计算机工程与应用,2004,40(16):84-86.

[12]杜陈艳,张榆锋,杨平,等.经验模态分解边缘效应抑制方法综述[J].仪器仪表学报,2009,30(1):55-59.