电控罗经的变传递系数阻尼方法

（海军驻上海地区水声导航军事代表室，上海 200136）

船用电控罗经在使用中，经常遇到这样的问题：在不同纬度下工作，其误差相差较大，特别是在动态环境下。传统理论认为，随着纬度的增加罗经误差也增大，这是属于罗经的机理性误差，所以一般电控罗经精度要求一般都含有secΦ 项。这是因为，在固定阻尼传递系数条件下，纬度越高，垂直阻尼作用越小，罗经效应越弱，经过稳定点时间长，动态误差越大；纬度低，其罗经效应越强，垂直阻尼作用越大，罗经效应越强，经过稳定点时间短。但罗经效应太强也容易引起振荡，相反延长了罗经找北时间。本文从电控罗经阻尼角度分析了误差相差大的根本原因，提出了电控罗经的变传递系数阻尼方法。使用恰当的阻尼，保证了较短的动态稳定时间和稳定的误差精度，弥补了secΦ 项带来的误差变化，并在某型电控罗经中得到成功应用。

1 电控罗经基本原理及模型

电控罗经是现代舰艇导航系统的必选设备，主要为舰艇提供稳定可靠的航向信息。它基于陀螺仪的基本特性：自由陀螺仪主轴的指向具有稳定性，即力图保持原先给予该轴的相对宇宙惯性空间的指向不变；当有外力矩作用在万向环上时，陀螺仪的动量矩H 将以最短的距离转向外力矩M的方向。将自由陀螺转化为陀螺罗经，就是要求陀螺仪主轴一旦偏离子午面，它能自己敏感出来，并施加相应力矩，使陀螺主轴自行回到并稳定在子午面内，保持指北精度。

电控罗经主要由陀螺仪、电磁摆、修正回路和跟踪回路组成。陀螺球若偏离子午面，在地球自转水平分量的作用下，陀螺主轴将偏离水平面，于是随动球与陀螺球之间出现水平失调角，水平信号器敏感此失调角后，产生失调信号，水平随动系统工作，使随动球转过一角度以跟踪主轴的运动。此时，固定在随动球东端的电磁摆也跟着倾斜一角度，输出比例于倾斜角的摆信号，此信号经控制系统放大，输给水平力矩器及方位力矩器。方位力矩器给陀螺施加方位控制力矩（找北力矩）。水平力矩器施加水平阻尼力矩，从而使陀螺主轴进行阻尼振荡而稳定在子午面内[1]。罗经稳定后，当船舶转向时，随动球同罗经座与船体一起转动，而陀螺主轴方位保持不动，仍指向子午面，于是随动球与陀螺之间便出现方位失调角。方位随动系统工作，使随动球相对罗经座转回，时刻跟踪陀螺球主轴位置。

某型电控罗经具体原理框图见图1，它采用垂直阻尼和纬度积分自动补偿方式。

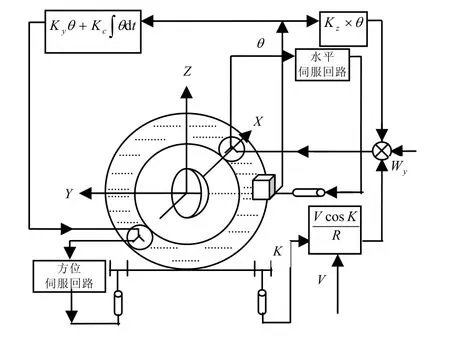
图1 模型电控罗经原理图

其中，陀螺力矩器施控方程为：

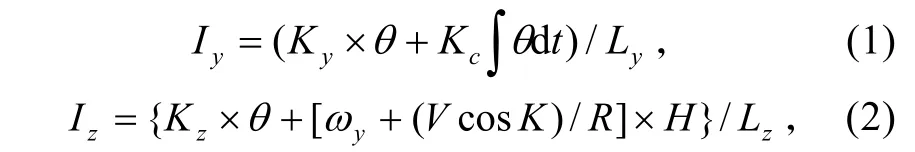
式中：Ly为方位力矩器力矩系数（g⋅cm/mA）；Lz为水平力矩器力矩系数（g⋅cm/mA）；H为陀螺角动量（g⋅cm⋅s）；Ky为方位伺服回路传递系数（g⋅cm）；Kz为水平伺服回路传递系数（g⋅cm）；Kc为积分系数（g⋅cm）；θ为电磁摆敏感角（rad）；ωy为陀螺漂移（rad/s）；V为航行速度（m/s）；K为航向角（rad）；R为地球半径（m）；Iy、Iz分别为方位和水平力矩器施矩电流（mA）。

2 变传递系数阻尼方法介绍

电控罗经陀螺仪在找北过程中，若仅仅靠方位回路，那么还不具备找北功能，它会绕着子午面上某个中心点连续不断地做椭圆运动。如果我们对陀螺施加一个附加力矩Mz，使主轴的椭圆振荡轨迹收敛，并稳定在子午线方向的平衡位置，就能稳定指北了，这就是阻尼的作用[2]。本系统介绍的是垂直阻尼，前文中的水平伺服回路就是我们的阻尼回路。阻尼作用的大小主要由水平伺服回路传递系数（阻尼回路传递系数）Kz决定。

在电控罗经的整机调试中，为达到最佳的静态和动态性能，阻尼的调整是一个不可缺少的重要项目。它主要用平均阻尼比来参照和度量。图2为电控罗经的稳定过程图。K0为拉偏航向（在调试中一般取5°），K为稳定点航向，K1为第一次过稳定点后的过冲最大航向，K2为第二次过稳定点后的过冲最大航向。

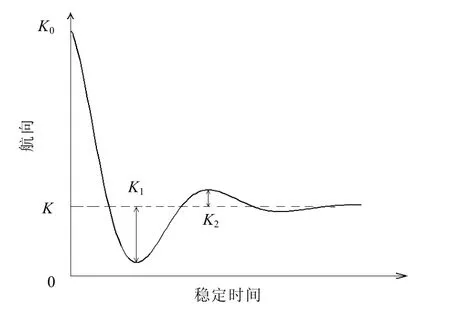
图2 电控罗经稳定过程图

现代电控罗经要求全球范围工作，运行纬度范围广并要求在工作范围保证一定的精度。

我们采用东北天坐标系，地球自转的水平分量ω1=ωecosϕ，若由于外界干扰，导致航向误差α，则 ω1可分解为沿载体X轴和Y轴方向分量[3]。其中X轴分量会引起陀螺主轴偏离水平面θ，角速度ω=ωecosϕsinα。

ωe固定，假设Kz固定，当有指向误差时，随着纬度ϕ的增大，cosϕ 较小，从陀螺力矩器施控方程可以看出，θ抬头（或低头）的速率较低，导致寻北力矩减小，寻北速度变慢，稳定时间拉长，精度降低；反之，在低纬度时，θ抬头（或低头）的速率较大，寻北力矩My也相应较大，这时又容易引起振荡，稳定时间同样拉长。这两种情况都会影响动态精度。因此，在罗经状态，在各种纬度下，为保证一定的寻北力矩而又不引起振荡，就不能使系数Kz保持恒定，这就是变传递系数阻尼方法的主要思想。

从公式 Mz=Kz×θ+[ωy+(V cosK)/R]×H可看出，在纬度ϕ 变大时，相同α的情况下，为保持罗经寻北精度，应使θ 减小变慢，使My积分项在较长时间内起作用，以保持较长时间的寻北力矩My。这时，应该减小系数Kz，从而陀螺回到水平位置的阻尼力矩Mz减小，从而保证了较长时间较大的陀螺寻北力矩；反之，应增大Kz，使θ 快速减小。

现代电控罗经均采用了数字控制，对参数的调整也更为自由和方便，这使得电控罗经的变传递系数阻尼方法的物理实现成为可能。

对于双态罗经，实际应用中，ϕ≥ ±70°时，罗经处于方位仪工作状态，此时，Mz=0。

在罗经工作状态，我们取系数 Kz=Kscosϕ，Ks为常值（罗经设定值），在赤道位置时 Kz=Ks，此时最大。Kz随纬度的增加而减小。

当ϕ=±69.9°时，Kz=0.34366K，为最小。

我们针对使用的陀螺球的动态特点，在不同纬度，采用不同动态方式，经过大量的静态、跑车和跑船试验，在积累大量实验数据的基础上，选取了常值Ks。

图3是电控罗经状态切换流程图，虚线部分为在传统罗经基础上采用变传递系数阻尼方法电控罗经流程需增加的部分。

图3 电控罗经状态切换流程图

在设计方案中，我们增设了速度、初始纬度、初始航向角信息输入和航向角数字发送通讯接口，使系统与外部设备的信息交流更加便捷；增加航向角转换模块和摆信号A/D转换，提高了系统数字化水平；输出有数字、模拟以及固态发送方式供用户选择；根据我们掌握的陀螺球的模型特性，控制电流的计算采用数字PID 方式，陀螺仪补偿由过去的模拟方式改成脉冲调宽控制方式（PWM），各种误差补偿通过数字计算和PWM技术实现，控制精度大为提高[4]。纬度ϕ 有两个来源，一个是外来输入；在没外来输入时，系统可依靠自动纬度积分得到。这样，系统保证了罗经状态下，在不同纬度下的基本一致的寻北能力和动态性能[5]。

3 试验结果

新型电控罗经采用全数字控制方法，力矩电流采用了脉冲调宽方式，提高控制精度；采用变传递系数阻尼方法的同时，设计出了一整套相应的调试方法，使阻尼系数的调试更为简单；设备的数字化使信息的输出也更为准确和方便；设备在长江口进行的航行试验中，取得了满意的精度，超出了我们的设计要求；在南到三亚，北至青岛的海域中进行的航行试验中，电罗经都能可靠工作并保证了基本一致的动态精度，进一步验证了我们当初的设计思想。

[1]许江宁.陀螺原理[M].北京:国防工业出版社,2005:132-135.

[2]黄德鸣.平台罗经[M].北京:国防工业出版社,1994:10-11.

[3]黄德鸣,程禄.惯性导航系统[M].北京:国防工业出版社,1986:16-19.

[4]潘新民.微型计算机控制技术[M].北京:人民邮电出版社,1988:216-219.

[5]张宁,胡渊.电控陀螺罗经改进[J].船舶,2008(1):42-46.