碟形飞行器复合控制系统的控制分配策略研究

刘 铁，杨 侃，文建国

（海军航空工程学院 a.飞行器工程系；b.研究生管理大队；c.科研部，山东 烟台 264001）

0 引言

现代飞行器由于气动布局的变化，大多采用多控制面结构，这样就产生了多种控制面组合方式。如何合理组合多种控制面，使飞行器能适应不同的飞行条件和飞行任务，同时在部分控制面发生故障情况下，仍然能通过剩余控制面的重新组合来协同控制飞行器运动，提高飞行器对故障及损伤的鲁棒性，已越来越多的引起国内外科研工作者的关注。

碟形飞行器呈圆盘形，是一种无尾无舵、翼身完全融合的非常规飞行器，它是一个高度非线性的系统，可以采用变质量矩控制与推力矢量控制相结合的方法实现它的飞行控制[1]。变质量矩控制与推力矢量控制构成的复合控制系统可以利用这两种控制技术的优点，形成复合优势，实现碟形飞行器的机动飞行控制，但同时也带来了一系列难题。难题之一就是如何处理一个高度非线性的多输入系统。论文首先对碟形飞行器的纵向运动方程进行简化，采用控制分配思想在结构上对碟形飞行器复合控制系统进行了优化，将设计过程分割成控制律设计和分配策略设计两个部分，再进行控制器设计和控制分配率设计，并进行仿真研究。

1 碟形飞行器纵向通道复合控制模型

通过对碟形飞行器（如图1所示）所受合外力和力矩的分析可以得到碟形飞行器动质心运动动力学方程、动质心运动学方程、绕动质心转动的动力学和运动学方程、以及角度关系方程等数学模型，这些非线性方程描述了碟形飞行器的基本运动。限于篇幅，论文不再一一列出。

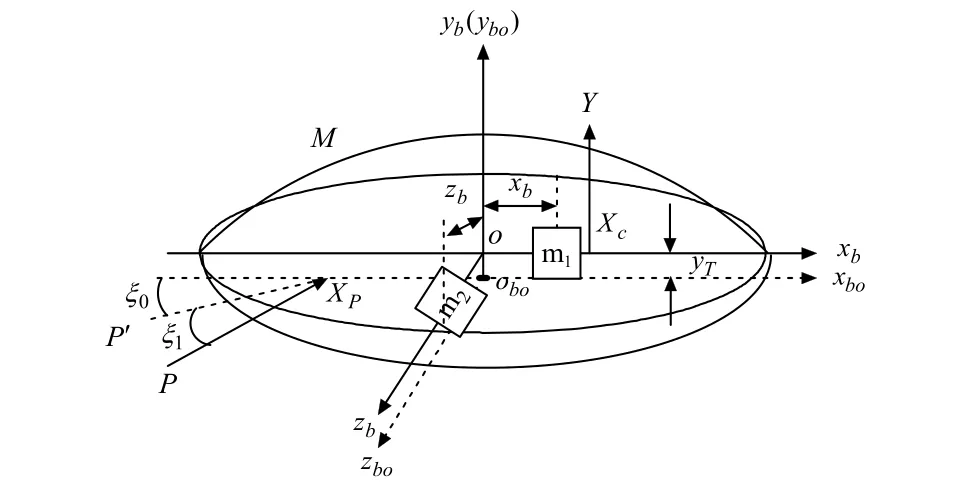
图1 一类碟形飞行器示意图

根据纵向运动假设，得到碟形飞行器纵向运动简化方程[2]

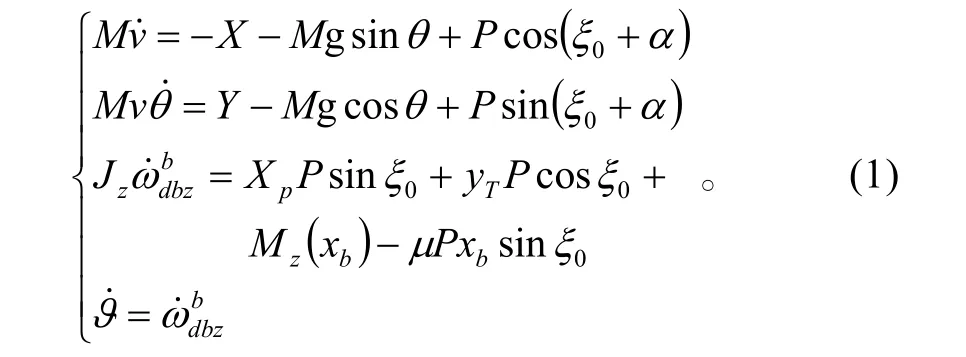
利用小扰动假设，且考虑对速度不进行控制，对式(1)进行小偏差线性化，把简写为ωz，得到纵向通道变质量矩/推力矢量复合控制线性化方程

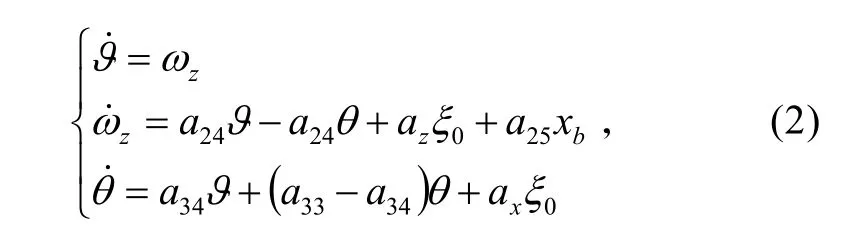
式中：a24、a25、a33、a34、ax和 az为模型线性化后基于基准弹道参数的动力学系数。具体数据由碟形飞行器实物模型的风洞试验所得。

2 复合控制分配技术简介

2.1 碟形飞行器复合控制分配系统的结构

碟形飞行器复合控制系统的总体结构如图2所示：首先，构造一个虚拟控制，针对这个虚拟控制设计控制律；然后，通过复合控制分配策略模块，将虚拟控制量恰当地分配给两个控制机构，由两个控制机构配合共同控制飞行器的姿态运动。按这种设计，控制系统的设计就分割成两个部分，即控制律设计和分配策略的设计[3-4]。

图2 碟形飞行器复合控制分配系统结构图

图2中，控制律的设计仍与一般系统的控制律设计相同。复合控制的分配策略应使整个控制回路从效果上等同于虚拟控制直接作用于系统。因此，对控制分配策略的设计有如下要求：

1）可以根据虚拟控制指令决定单独或者同时使用各个控制机构；

2）在各个控制进行切换时，不应影响控制器的稳定性。

对于控制分配，国内外的科研工作者取得了很多的研究成果。这些方法归结起来主要有非优化的控制分配方法和优化的控制分配方法。

2.2 非优化的控制分配方法

非优化的控制分配方法有广义逆方法、串接链方法和直接分配方法等。

2.2.1 广义逆控制分配方法

广义逆方法[5-9]包括伪逆法、加权伪逆法及所谓最优的广义逆分配方法等。伪逆法的思想是取控制量的二次范数（能量函数）为优化指标。即：

式中：B为控制效率矩阵。它的最优解为：u=BT(B BT)−1v=B+v，其中 B+称为B的伪逆。

伪逆法在所有飞行条件下各个控制量都参与控制，因此可以减少气动舵面总的偏转量，延缓质量滑块位移和推力矢量舵面进入饱和的时间，但是却可能因为饱和而达不到最大可用力矩。

加权伪逆法是对伪逆法的一种推广，对于要求的控制力矩，按照使用侧重点的不同，对各个控制量进行加权。考虑到控制约束的广义逆法有多级广义逆和重新分配伪逆法，这些方法在期望目标可达时，一般可以求出可用的控制，而当期望目标不可达时，误差将剧烈增大。

2.2.2 串接链控制分配方法

串接链方法[10-11]将整个操纵面分为若干组，每一组可以产生所期望的力矩。其分配方式描述如下：

将m个控制输入分为M组，并将相应的控制效率矩阵分为M组，即

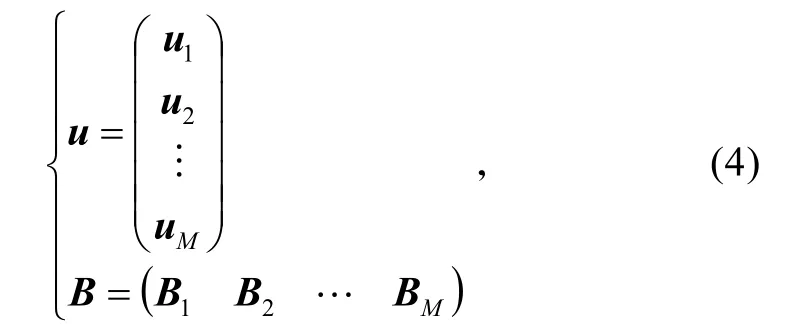
则控制分配问题便是求解下式：

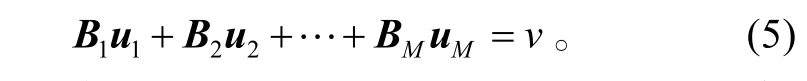
首先用第一组操纵面来实现伪控制输入v，使得 B1u1=v，如果用第一组不可实现，则依次使用其余组操纵面来是实现控制分配。其过程控制表示：

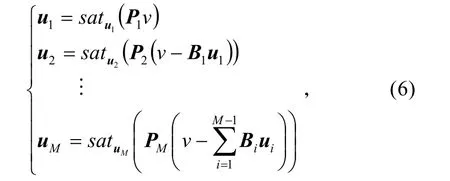
式中：BiPi=I，satui(⋅)代表第i个操纵面的位置约束和速率约束。

2.2.3 直接分配方法

直接分配方法[12-15]可以描述成如下的最优分配问题：设表示转矩空间φ 中的单位向量，即

给定控制效率矩阵B，带约束的控制向量集合Ω 和期望转矩向量确定u∈Ω，使u 产生的转矩向量在方向上的幅值最大。如果这样求得的u 产生的转矩向量的幅值超过了期望转矩向量的幅值，可对u 乘以一个衰减系数，使两者相等。其物理意义为：在控制限制范围内，确定最优控制向量u，使在给定方向上的转矩最大。

2.3 优化的控制分配方法

2.3.1 基于线性规划的直接最优分配方法

控制分配的线性规划问题可描述为如下形式：

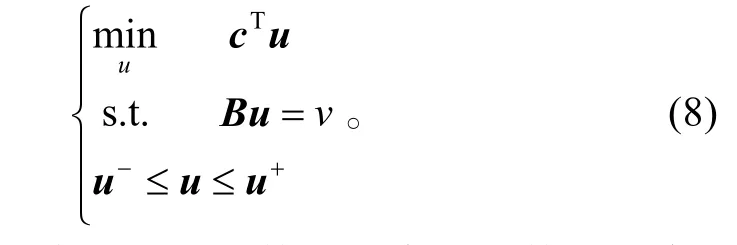
式(8)包括代价函数、等式约束和不等式约束3个重要元素，这里规划指标取控制量的线性函数，等式约束定义了控制变量的解空间，而不等式约束则体现了执行机构的位置和速率限制。

2.3.2 基于二次规划的直接最优分配方法

二次规划方法[16-17]在控制分配中可以表述为：

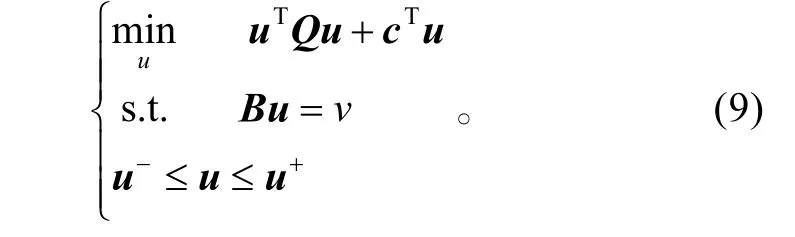
二次规划方法和线性规划方法的区别在于代价函数的不同。线性规划取控制量的线性函数，二次规划取控制量的二次函数。

当执行机构发生饱和时，满足条件的最优解位于可达转矩集之外。此时，求解过程将会放松等式约束，而不等式约束却保持不变，转而寻求次优解。二次规划方法可以灵活利用代价函数和约束条件，对某些控制量进行加权或者惩罚，从而迫使系统遵循其他特定的约束条件，解决复杂控制分配问题。当执行机构出现故障或失效时，二次规划方法可以同时更新控制效率矩阵B以及等式和不等式约束，使系统重构。例如基于二次规划方法的方向保持法（Direction Preserving Method）在等式约束不能满足时，通过引入一个比例系数 0≤σ≤1来修改期望转矩矢量的大小，但是却保持期望转矩矢量的方向，该方向和可达集边界的交点即为所求解。符号保持法（Sign-Preserving Method）则对于各个轴的期望转矩分别引入一个比例系数 0≤σi≤1，仅仅改变其中某些期望转矩的大小，从而构成一个新的期望转矩矢量，但是符号却没有改变，从而更大限度地利用各个控制量。此外，基于频率加权的二次规划方法，考虑执行机构的频率，采用对特定控制量进行频域加权的方法，可在频域实现控制量的合理分配。

3 仿真研究

3.1 非优化的控制分配方法

这里仅用广义逆控制分配方法进行仿真研究。采用PD控制作为虚拟控制。根据文献[18]知

式中：M是俯仰力矩。

模型的动力学系数见表1。执行机构时间常数0ξτ=0.03 s，bxτ=0.03 s。推力矢量角约束为−30～30°，滑块滑动距离约束为−0.45～0.45 m。

表1 简化模型的动力学系数

1）当输入 ϑpr=1°（单位阶跃信号）时，单独控制和复合控制的响应曲线如图3所示。

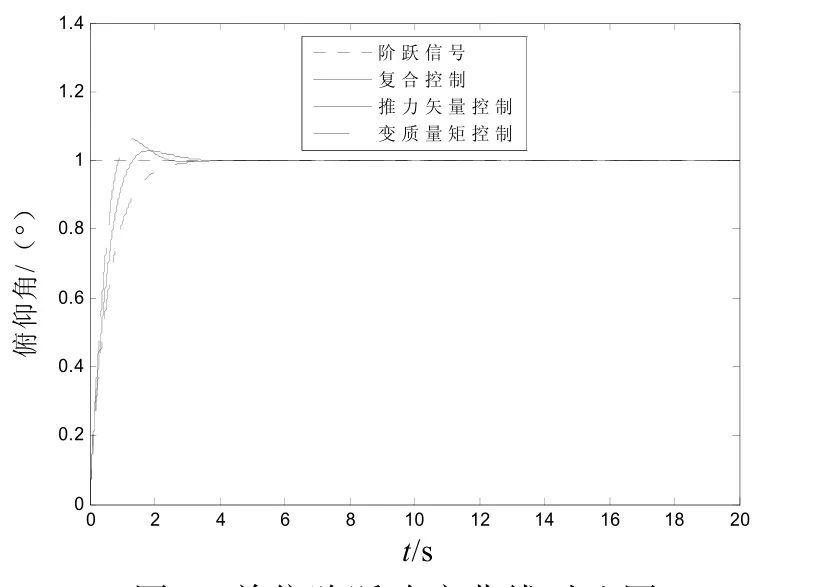
图3 单位阶跃响应曲线对比图

从图中可以看出，复合控制的动态性能介于两者之间。图4和图5是控制分配系数变化曲线。

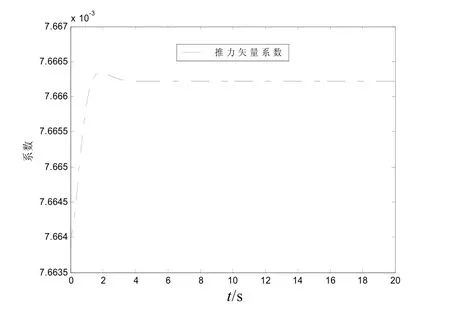
图4 推力矢量系数变化曲线

图5 变质量矩系数变化曲线

从图4、5中看出，推力矢量系数稳定在0.007 6，而变质量矩系数稳定在0.032 2，大约是推力矢量系数的4倍。

2）考虑控制面发生故障的情况。在t=10 s时，变质量矩控制系统失效，输入为ϑpr=1°（单位阶跃信号），系统的响应曲线如图6所示。

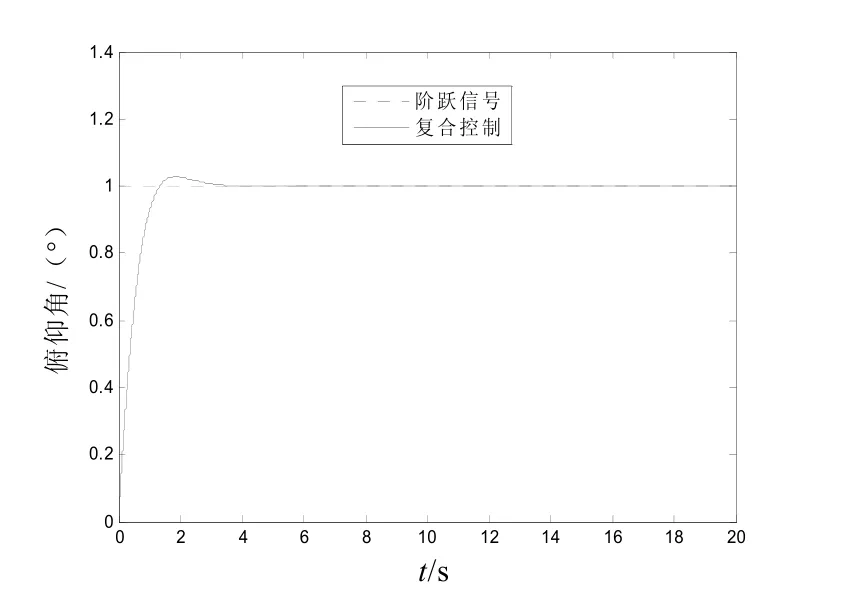
图6 发生故障情况下单位阶跃响应曲线

从图6中可以看出，故障对控制系统基本没有产生影响。

图7和图8是控制分配系数变化曲线。

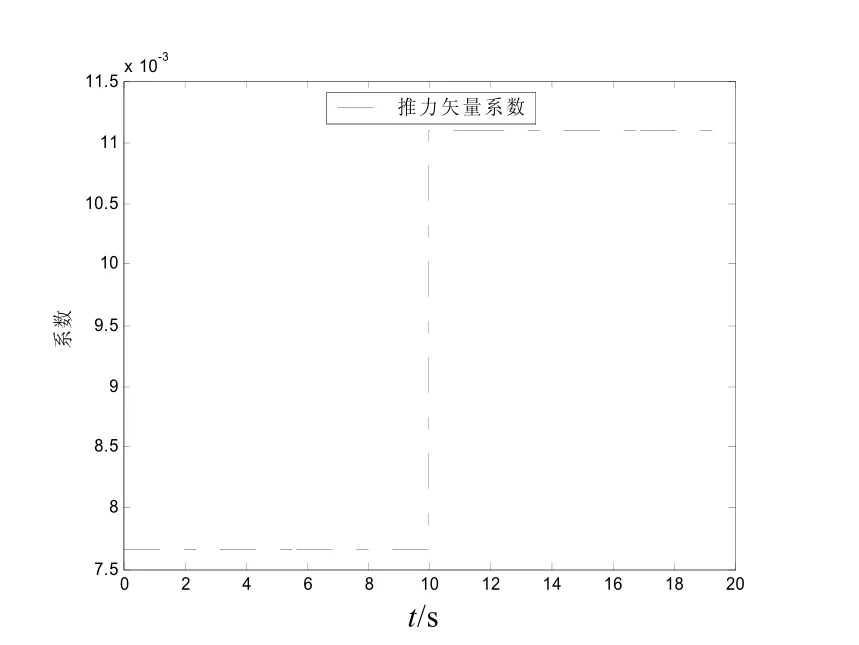
图7 发生故障情况下推力矢量系数变化曲线

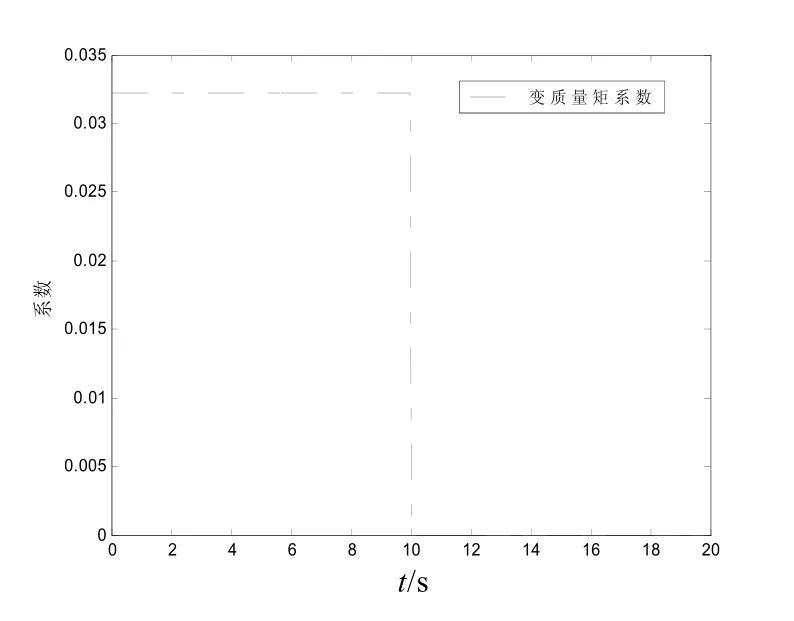
图8 发生故障情况下变质量矩系数变化曲线

3.2 优化的控制分配方法

这里仅用基于二次规划的直接最优分配方法进行仿真研究。从2.3.2节分析可知，它本质上是一个目标规划问题，约束条件Bu=v是一个软约束，它可以化为一个目标约束，本文用Matlab 中的fgoalattain函数来求解。模型的动力学系数见表1。执行机构时间常数 0ξτ=0.03 s，bxτ=0.03 s。推力矢量角约束为−30°到30°，滑块滑动距离约束为−0.45m到0.45 m。仿真结构图如图2所示。

取Q=I，c=0，当输入 ϑpr=1°（单位阶跃信号）时，单独控制和复合控制的响应曲线如图9所示。

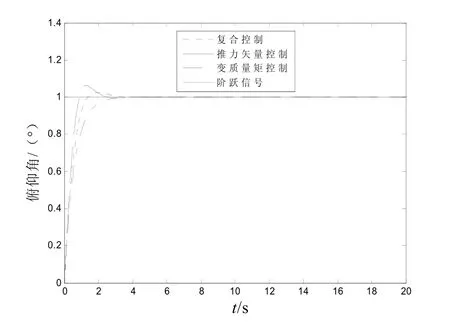
图9 单位阶跃响应曲线对比图

从图9中可以看出，与广义逆控制分配方法类似，复合控制的动态性能介于两者之间。图10和图11是控制分配系数变化曲线。从图10、11中可以看出，在调节时间内，推力矢量系数大约稳定在0.008，而变质量矩系数大约稳定在0.033 5，这与广义逆控制方法结果相近；之后，控制分配系数就在稳定值附近小幅震荡。

控制量变化曲线如图12、13所示。

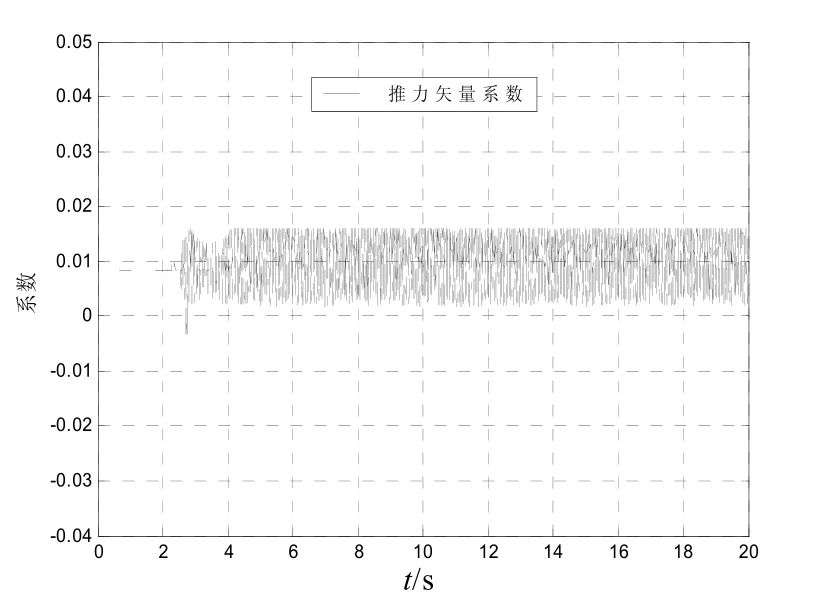
图10 推力矢量系数变化曲线

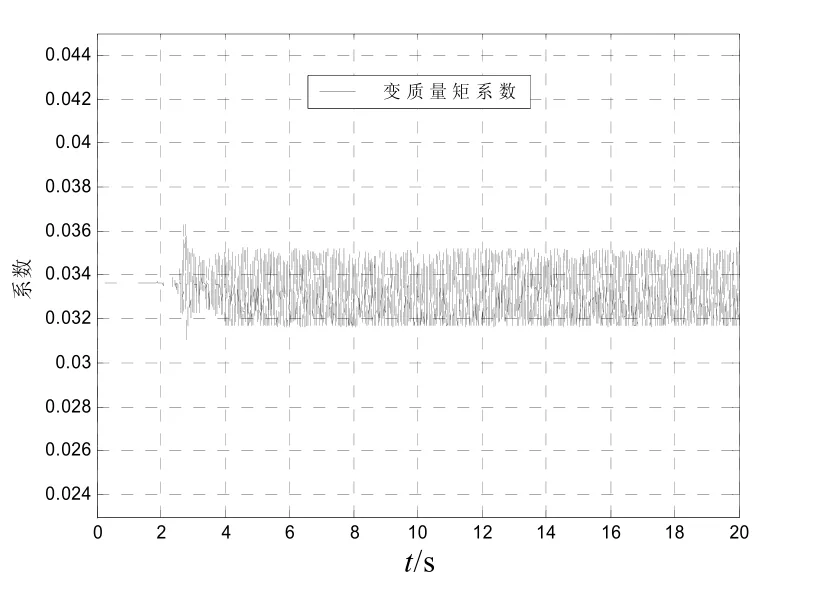
图11 变质量矩系数变化曲线

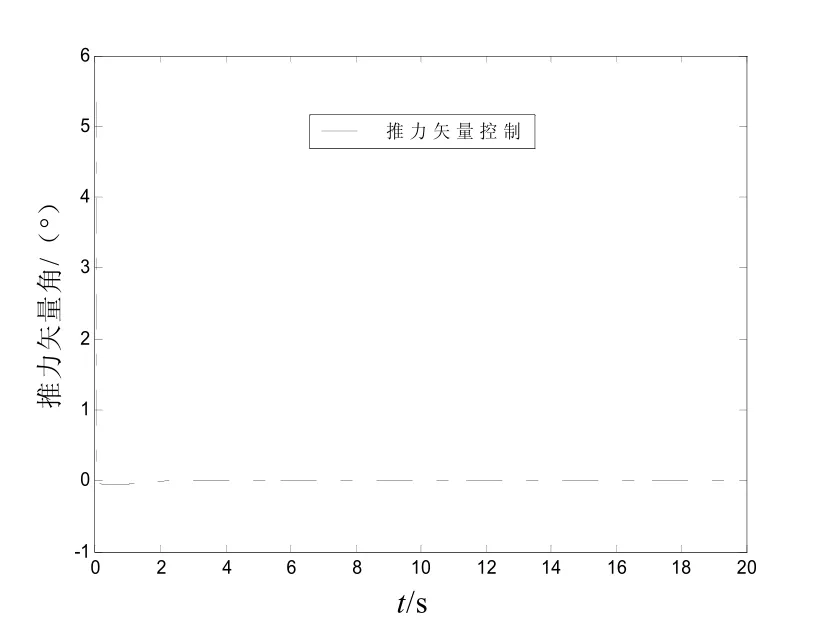
图12 推力矢量控制的控制量变化曲线

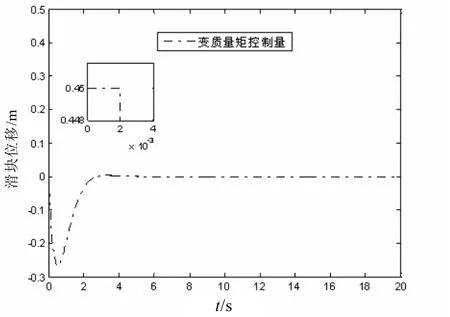
图13 变质量矩控制的控制量变化曲线

从图13中可以看出，变质量矩控制在初期有一段饱和状态，且在整个控制过程中占主导地位。

4 结论

本文采用控制分配思想在结构上对碟形飞行器复合控制系统进行了优化，将设计过程分割成控制律设计和分配策略设计两个部分，分别采用了广义逆控制分配方法和基于二次规划的直接最优分配方法进行了仿真研究，两种方法各有优缺点：广义逆控制分配方法原理简单，解算速度快，便于实时控制，但它没有考虑约束条件的影响；基于二次规划的直接最优分配方法在求解的过程中已经考虑了控制量的饱和约束，所以在仿真的过程中不用加饱和环节，简化了控制系统的结构，但它的求解时间较长，在实际应用中，可能达不到实时控制的要求。

[1]王军生,徐胜红,刘海波,等.碟形飞行器复合控制分配策略的设计与分析[J].战术导弹技术,2006(3):69-73.

[2]冯国虎.碟形飞行器复合控制中的控制分配策略[J].系统仿真学报,2008,20(4):970-973.

[3]徐胜红,盛忠培,顾文锦.碟形飞行器复合控制的非线性分配策略研究[J].弹箭与制导学报,2006,26(1):8-11.

[4]程凤舟,万自明,陈士橹,等.防空导弹直接力与气动力复合控制系统设计[J].飞行力学,2003,21(2):49-52.

[5]RANEY D L,MONLNOMERY R C.Flight control using distributed shape-chance effector arrays[R].AIAA-2000-1560,2000.

[6]REINELSPERNERW C.BANDA S S.Nonlinear simulation of a modified F-16 with full-envelope control law[J].Control Engineering Practice,1998,17(6):309-320.

[7]BORDINNON K.Constrained control allocation for systems with redundant control effectors[D].Blacksburg.VA:Virninia Polytechnic Institute and State University.1996.

[8]EBERHARDT R,WARD D.Indirect adaptive flight control of a tailless fighter aircraft[C]//Proceedings of the AIAA Guidance,Control,and Dynamics Conference.Portland.OR,1999:466-476.

[9]VIRNIG J,BODDEN D.Multivariable control allocation and control law conditioning when control effectors limit[C]//Proceedings of the AIAA Guidance,Navigation,and Control Conference.Scottsdale,AZ,1994:572-582.

[10]BUFFINGTON J M,ENNS D F.Lyapunov stability analysis of daisy chain control allocation[J].Journal of Guidance,Control,and Dynamics,1996,19(6):1226-1230.

[11]TEEL A R,BUFFINGTON J M.Anti-windup for an F-16's daisy chain control allocate[R].AIAA-1997-3606.1997.

[12]DURHAM W C.Constrained control allocation[J].Journal of Guidance,Control,and Dynamics,1993,16(4):717-725.

[13]DURHAM W C.Attainable moments for the constrained control allocation problem[J].Journal of Guidance,Control,and Dynamics,1994,17(6):1371-1373.

[14]DURHAM W C.Computationally efficient control allocation[J].Journal of Guidance,Control and Dynamics,2001,24(3):519-524.

[15]PELERSEN J,BODSON M.Fast control allocation using spherical coordinates[R].AIAA-1999-4215.1999.

[16]PELERSEN J,BODSON M.Constrained quadratic programming techniques for control allocation[C]//Proceedings of the 42ndIEEE Conferences on Decision and Control.Maui,Hawaii,USA,2003.

[17]SIMMONS A T.Control allocation techniques using existing and novel quadratic programming algorithms[D].Auburn University,2003.

[18]MICHAEL W OPPENHEIMER,DAVID B DOMAN.A method for including control effector interactions in the control allocation problem[R].AIAA-2007-6418.2007.