一种多分量chirp信号阵列检测新方法

（海军航空工程学院 电子信息工程系，山东 烟台 264001）

Chirp类信号是信号处理领域的常见信号之一，不管是在自然界的天然信号中，还是人为产生的信号中，都大量存在。因此，多分量chirp信号的检测和参数估计一直受到人们的关注。近年来随着分数阶傅里叶变换理论的迅速发展而产生了多种基于分数阶傅里叶变换的多分量chirp信号检测和参数估计算法[1-7]。该类方法能够有效实现chirp信号的同时四参数估计，性能分析和仿真结果都证明其检测效果和估计精度均优于原有时频类算法。不过，该类算法的现有研究成果均针对的是单阵元信号，而随着天线技术的发展，目前雷达、通信等许多系统中都采用了阵列天线来提高系统性能。因此，本文研究了如何利用阵列信号处理技术来提高现有算法[1]的检测和参数估计性能。

1 预备知识

1.1 信号模型

本文所用模型如下：

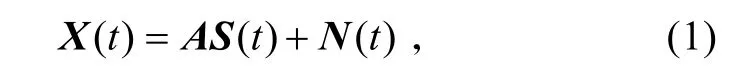
式中：S (t)=[s1(t),…,sN(t)]T为N个源信号构成的N维向量；X(t)=[x1(t),…,xM(t)]T为M 维观测数据向量，其元素是M个传感单元的输出信号；M×N (M≥N)维矩阵 A=[a1,…,aN]称为混合矩阵，其元素表示信号的混合情况，列向量 ai=[ai1,…,aiM]T代表第i个信源的空间特性；是M×1 维噪声向量。

式(1)的含义是N个源信号 S (t)通过空间特性为A的阵列后得到M 维观测数据向量 X (t)。为简化讨论，假定=M，这个假设并不会影响下面的讨论结果。

1.2 基于分数阶傅里叶变换的Chirp信号参数估计

多分量chirp信号可用以下模型表示：

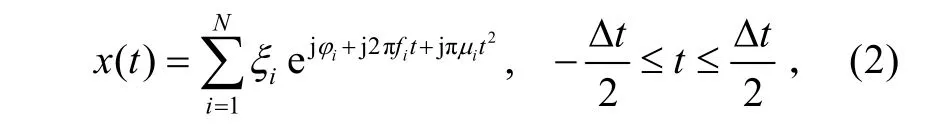
式中：iξ为幅度；fi为中心频率；iµ为调频率；iϕ为初相。

分数阶傅里叶变换（FRFT）定义可参看文献[8]。利用分数阶傅里叶变换与时频分布的关系，可实现chirp信号的检测与参数估计[1]：

上述方法可以推广到多分量chirp信号的检测与参数估计，当多分量信号之间强度相差较大时，可采用从强到弱逐个消去的方法来抑制强分量对弱分量的影响[1]。但前提条件是多分量chirp信号之间的强度相差较大，弱分量对强分量的干扰很小，而能够较为准确地依次消去强分量。但是，在实际应用中上述条件往往难以保证，尤其是当信号分量较多，各分量之间的强度相差不大，且参数相近时，式(5)的取模运算会导致各分量间的相互影响增强，此时多分量之间的相互干扰会大大降低检测和参数估计的性能[9]。

为了解决这个问题，本文利用天线阵列通过分数阶傅里叶域阵列加权来抑制噪声和干扰项的影响，从而有效提高原有方法的性能。

2 分数阶傅里叶域阵列加权

因为噪声也可以看作是某个我们并不感兴趣的源信号，也就是说，式(1)中的X(t)可以看成为N+1个源信号通过混合矩阵A的产物。那么从分析多分量信号间的相互干扰这个角度出发（将噪声也作为源信号进行分析），可以将式(1)简化表示为：

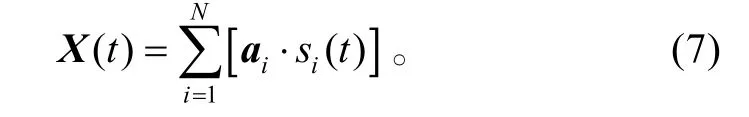
式(7)中为了表达式的简洁，求和符号的上标仍然用N表示。那么第k个传感器的输出为：

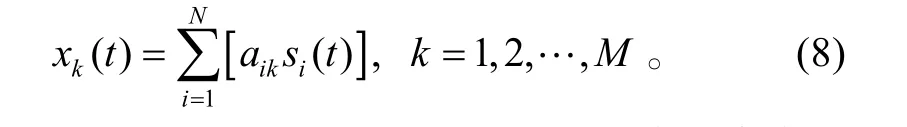
由于FRFT是线性变换，那么对于单个传感器输出xk有：

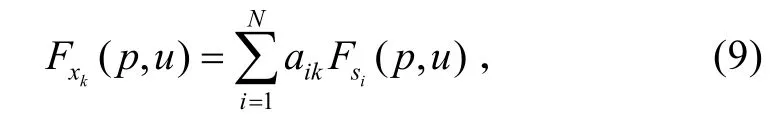
则

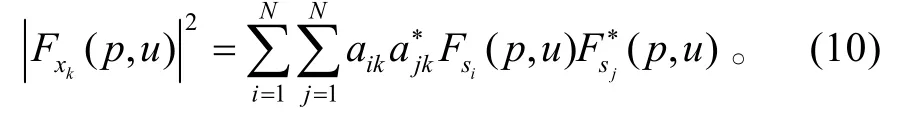
对天线阵各单元输出信号进行平均后可得：

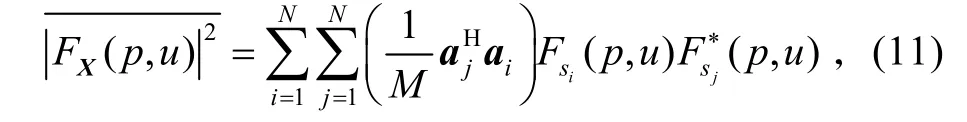
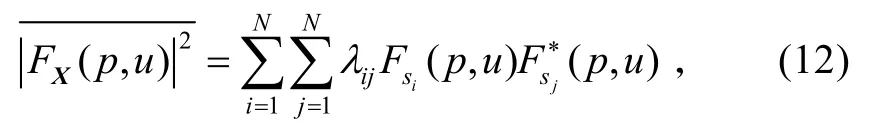
式中：

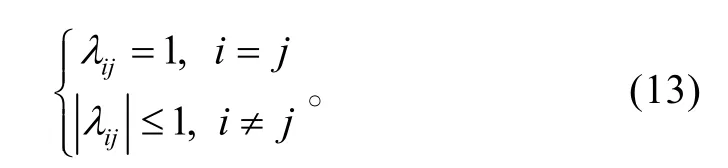
上式表明，天线阵各单元输出信号进行平均后的FRFT模平方是每个源信号的FRFT模平方和不同源信号之间FRFT 干扰项的线性组合。

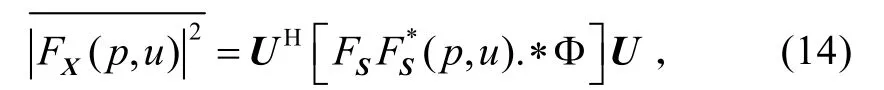
式中：“.∗”表示矩阵中对应元素的相乘；U是N×1维的单位向量；

矩阵 FSFS*(p,u).∗Φ中，对角元素代表的是每个源信号的FRFT模平方，非对角元素是第i个源信号的FRFT 和第j个源信号FRFT 共轭的乘积，即干扰项。

该矩阵每个元素前也都有一个加权系数 λij，当i=j时，λij=1；当i≠j时，

也就是说，矩阵中对角元素的加权系数均为1，非对角元素其加权系数的模均小于1。这样，通过对天线阵各单元输出信号进行平均便能够很好地抑制不同源信号之间的相互干扰。

3 算法

根据前述内容，可以得到新的检测和参数估计算法步骤为：

第一步，对每个传感单元的输出信号求取其FRFT模平方；

第二步，对第一步所得到的各阵元结果进行求和平均，通过阵列平均来抑制干扰项和噪声；

第三步，根据式(5)、(6)，在(p,u)平面内对所得到的FRFT模平方平均值进行两级二维搜索，由峰值点位置得到最强信号分量（i=1）的参数估计值

第四步，利用参数估计值恢复出第一个信号分量为：

第六步，将第五步结果代入第三步，重复进行上述步骤，依次得到其余的信号分量估计值，直至剩余的FRFT模平方平均值的峰值不再超过预定阈值。

4 仿真

本文仿真中采样频率为1 000 Hz，采样点数为1 000，阵元个数分别取1、4、8。所用两个chirp信号分别为：

其空间到达方向分别为π/8 和5π/12。

不妨设 s1(t)为有用信号，s2(t)为干扰信号，则干信比ISR=20lg (ξ2ξ1)，变化范围−16 dB～0 dB。

图1给出了阵元数分别是1、4、8的参数估计误差平方随干信比的变化曲线。从曲线上可以看出，干扰很弱时单阵元和多阵元平均的性能接近。但是，随着干扰强度的增大，单阵元的估计误差迅速增大，而多阵元平均的估计误差虽增长但缓慢得多，并且，阵元个数越多，估计精度越高。

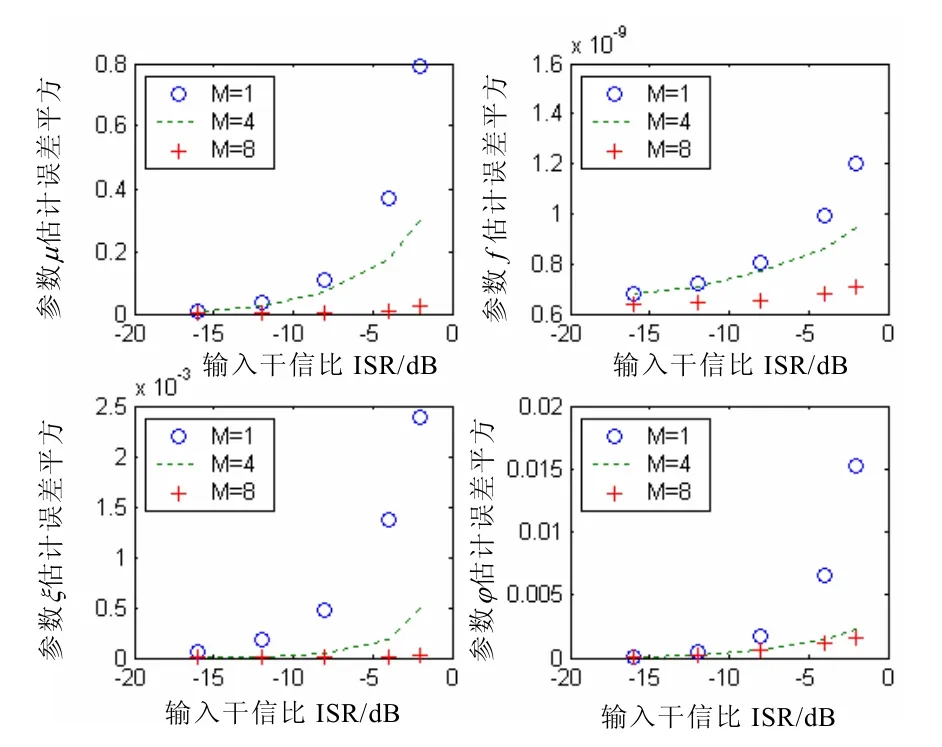
图1 多参数的估计误差曲线

接下来进一步定量说明所提算法的有效性，仿真中采用8 阵元均匀线阵，采样频率为100 Hz，采样点数为100，所用信号为s (t)=s1(t)+s2(t)+s3(t)，其中：

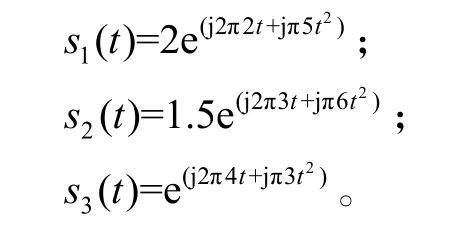
当只用一个阵元来对 s1(t)进行参数估计时，误差分别为：

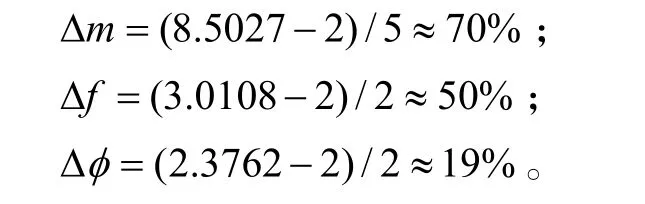
∆m、∆f、∆φ分别表示调频率、初始频率和幅度的估计误差。当采用本文所提方法时，误差分别是：

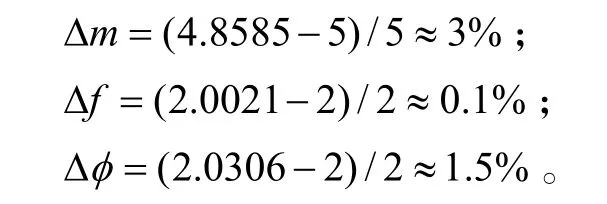
从仿真结果可以看出，本文方法有效地抑制了多信源间的相互干扰。

5 结论

本文提出了一种基于分数阶傅里叶域阵列加权的多分量chirp信号检测和参数估计新方法。仿真结果证明了该方法的有效性和实用性。和单阵元检测方法相比，新方法大大提高了检测和参数估计的性能，尤其适用于信噪比较低、信号分量个数较多、各分量强度相差不大且参数相近的情况。

[1]QI LIN,TAO RAN,ZHOU SIYONG,et al.Detection and paramter estimation of multicomponent LFM signal based on the fractional Fourier transform[J].Science in China:Ser.F,Information Science,2004,47(2):184-198.

[2]董永强,陶然,周思永,等.含未知参数的多分量chirp信号的分数阶傅里叶分析[J].北京理工大学学报,1999,19(5):612-616.

[3]周刚毅,叶中付.线性调频信号的调频斜率估计方法[J].中国科学技术大学学报,2003,33(1):34-38.

[4]赵兴浩,陶然,周思永,等.基于Radon-Ambiguity变换和分数阶傅里叶变换的chirp信号检测及多参数估计[J].北京理工大学学报,2003,23(3):371-374,377.

[5]李靖,王树勋,汪飞.基于分数阶傅里叶变换的chirp信号时频分析[J].系统工程与电子技术,2005,27(6):988-990.

[6]朱全银,邓建平.基于分数阶傅里叶变换的线性调频干扰抑制[J].探测与控制学报,2009,31(1):10-14.

[7]金燕,黄振,陆建华.基于FRFT的线性调频多径信号分离算法[J].清华大学学报:自然科学版,2008,48(10):1617-1620.

[8]陶然,邓兵,王越.分数阶傅里叶变换及其应用[M].北京:清华大学出版社,2009.

[9]邓兵,陶然,曲长文.分数阶Fourier 域中不同调频率多分量chirp信号间的遮蔽分析[J].电子学报,2007,35(6):1094-1098.