μ综合中的D-K迭代算法

何朕， 姜晓明， 孟范伟， 周荻

（哈尔滨工业大学控制科学与工程系，黑龙江哈尔滨 150001）

0 引言

对于结构不确定性，需要用结构奇异值μ来描述系统的性能，而μ综合法［1－2］是处理参数不确定性系统鲁棒设计的一种有效的手段［3－4］。μ综合中控制器和μ值的求取需要采用迭代的方法来进行。虽然D-K迭代在Matlab中有现成的命令可供使用［5］，但是这些命令的使用需要设计者与之互动，例如初始值的设置是否合理，迭代过程是否正常，是否还要进行下去等。为此需要对这些命令在迭代过程中所产生的数据有充分的了解。可是一般的手册或是非专业性的Matlab介绍都做不到这一点。本文从D-K迭代的理论出发，详细分析了迭代过程中所产生的数据，使之排除设计过程中的一些似是而非的结论，引导设计者正确进行D-K迭代来得出一个满意的鲁棒设计结果。本文将结合一个具体的μ综合例题来进行介绍，使所讨论的问题更为具体，以便于了解和掌握。

1 结构奇异值和μ综合

本文主要讨论μ综合的算法问题。为节省篇幅，一些基本概念和定义将随例子作些必要的说明而不单独进行讨论。这里的例子是一个卫星姿态控制系统，要求在参数摄动10%下保证系统的性能，即鲁棒性能问题。

设系统的运动方程［6］

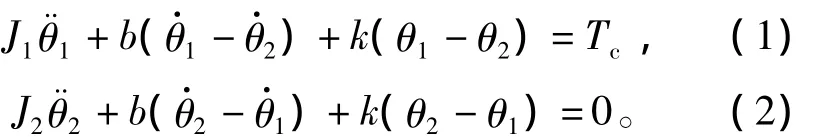
式中:J1代表卫星本体，J2为卫星上的光学系统，二者是由连杆系统相连，J1=1，J2=0.1;k和b的名义值为k0=0.091，b0=0.000 36。本例取自文献［6］，不过为了能突出本文的问题，b0取了一个更小的值。Tc为控制力矩，设输出量为 θ2，若选择 x=［θ2θ1］T作为状态变量，并设 Tc=u，则由式（1）和式（2）可写得状态空间表达式为

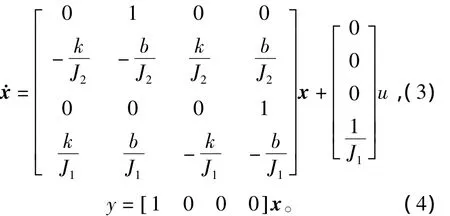
在下面的计算中按统一编号，输出y就是图1中的y2，而图1中的u2就是式（1）中的u。设连杆的结构参数随温度而有变化，即

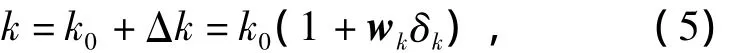
式中k0为名义值;δk是界为1的不确定性，|δk|≤1;wk为相对变化范围，设wk=10%。

本例中b的值与k有关，按泰勒级数展开得

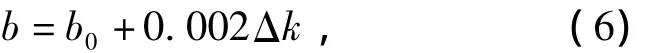
式中b0为名义值。

将上述的参数摄动代入式（3）可得

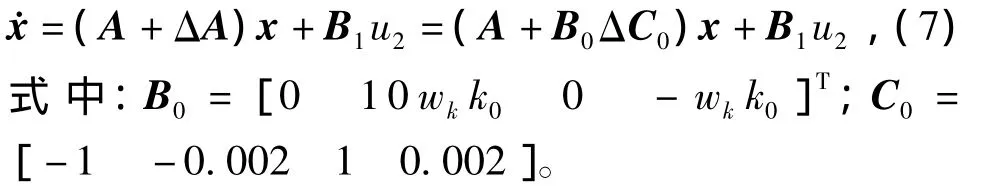
这里采用统一的符号Δ来表示不确定性，Δ=δk。式中C0x表示作用到不确定性Δ的信号，z3=C0x（见图1）。Δ的输出u3通过B0与状态阵A相加。这样，当将不确定性单独列出时，系统的状态方程式就可以用矩阵形式表示为

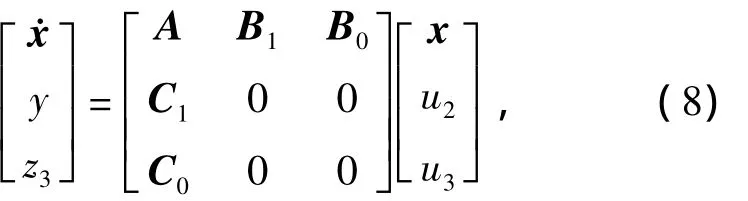
而不确定性的方程式为

式（8）表明，当考虑参数摄动时，卫星对象的输入将由u2和u3两部分组成，输出也可分为y2和z3两部分，而表示参数摄动的不确定性Δ则和对象形成一种上线性分式变换的结构，如图1所示。

图1中的W1、W2和W3均为常规的H∞设计中的权函数，为

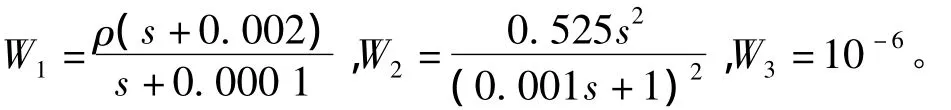
式中的ρ应在μ综合设计中取最大值，举例中的数据采用的是优化设计最后一步的数据，此时ρ=0.11。

为了说明鲁棒性能问题，先将对象P与权函数合写成广义对象G，将图1整理成图2的形式。图2所示，即鲁棒性能问题的框图，要在存在参数摄动Δ时，要求从输入w到输出z的H∞范数小于1，即

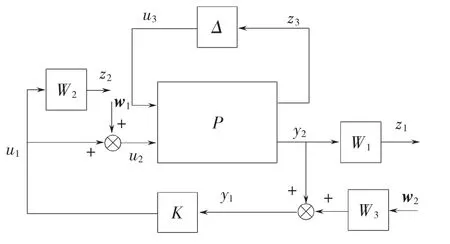
图1 系统的框图Fig．1 System block diagram

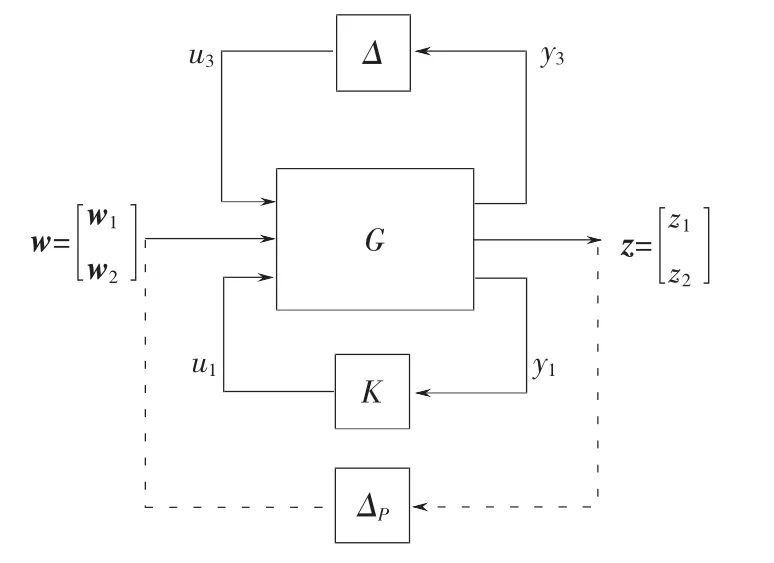
图2 鲁棒性能问题Fig．2 Robust performance problem

注意到这个鲁棒性能要求也相当于用一个摄动块ΔP跨接在w、z端上的稳定性要求，如图中虚线所示，‖ΔP‖∞≤1。设用M来表示控制器K回路闭合后的对象，M=Fl（G，K），则这个鲁棒性能要求就完全等价于M在块对角结构的摄动Δ和ΔP下的鲁棒稳定性问题，如图3所示，或者写成一个更为紧凑的形式，即

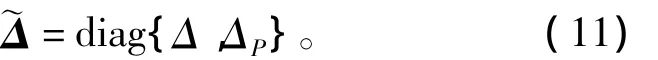
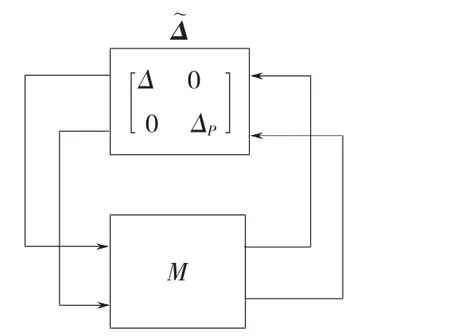
图3 结构不确定性问题Fig．3 Structured uncertainty problem

这种块对角结构的不确定性称为结构（化）不确定性。如果~Δ不是块对角结构，则根据小增益定理，图3系统稳定的条件就是¯σ［M］≤1或‖M‖∞≤1。但是在现在的结构不确定性下，这个奇异值（或H∞范数）条件就有保守性了，为此需要定义一个新的量，称为结构奇异值μΔ（M）。这里下角标Δ表明结构奇异值与具体的不确定性的结构形式有关，不过一般书写时也常略去这个下角标。与常规的H∞设计中要求系统的最大奇异值的最小值小于1的概念类似，图3系统稳定的充要条件为

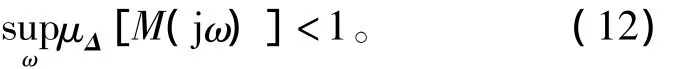
根据式（12）的要求来设计控制器K的方法称为μ综合。

结构奇异值μ一般是通过上界来进行计算的。而且是利用一个标定阵D来获得一个更紧密的上界［2］，即

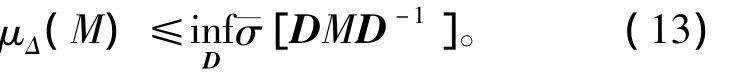
这样，当用μ综合法时就是要求解下列的优化问题

注意到这里的D也是一个频率函数D（ω），所以这个优化问题是一个二参数的极小化问题

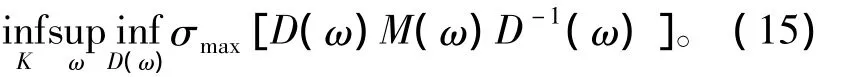
式（15）表明，当D（ω）确定时，这是一个H∞优化设计问题，可求得K。当K确定时，每一个ω下求D，使 ¯σ［DMD－1］最小，D 代入后再重复第一步，求解H∞优化设计问题。这样交替进行的求解过程称D-K迭代。

2 D-K迭代的计算

进行D-K迭代时，Matlab的 μ-Tools中有2个D-K迭代命令可供使用:

1）利用对话框命令dkitgui;

2）利用脚本文件dkit。这个命令实际上是调用一个已编好的程序，只要使用者对变量进行初始化即可。

这两个命令实质上是一样的，利用对话框命令时，设计时的互动性更强一些，设计者可一步一步地了解迭代的进程和选择必要的参数。如果不需要更多的互动，则可以选用dkit，可以较快地得出结果，甚至可以选用自动迭代的方式直接给出结果。

下面主要是结合dkit的结果来进行说明。在进行D-K迭代前首先需要建立广义对象的系统阵。第一步需要将图1中的各部分用pck或nd2sys命令转换成系统阵的形式，因为在H∞操作中是不支持传递函数的，都采用由状态空间表达式所构成的系统阵的形式。接下来将这些环节通过sysic命令连接成广义对象，具体的操作步骤可以参见文献［5］。广义对象如图4所示。需要强调的是，利用sysic建立广义对象G时的输入输出变量顺序都应该按图2所示的从上到下的顺序进行排列，否则可能得到的是另外一个广义对象。

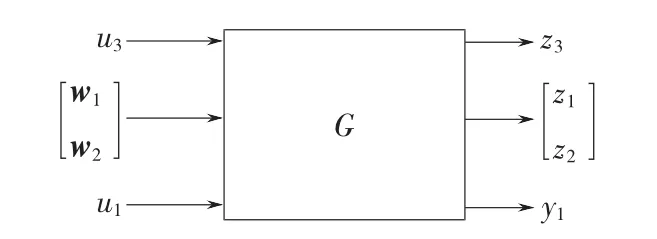
图4 本例中的广义对象Fig．4 Interconnection of the generalized plant

要将这个广义对象接入到dkit的M文件中，还需要定义一组用户变量，包括广义对象的名称G、对象测量输出y的维数、控制输入u的维数、摄动块的结构参数以及频率范围。在定义了用户变量后，若将这个文件保存为并命名为satellite－dk．m。在命令窗口输入下述命令，即

这样，dkit中就有了用户所定义的变量，就可以运行了。

作为例子，在进行相应的变量定义后，通过dkit进行D－K迭代，第一次的迭代过程如表1所示，得γ值为65.625。

表1 第一步γ迭代的结果Table 1 First γ-iteration results

表1中λ1、λ3分别代表Hamilton阵H∞和J∞特征值的最小实部，而λ2、λ4分别表示Riccati方程解X∞和Y∞特征值的最小实部，ρ表示 X∞Y∞的谱半径。这第一步中的标定阵D=I，在综合控制器K（s）的γ迭代中求解的就是H∞优化问题

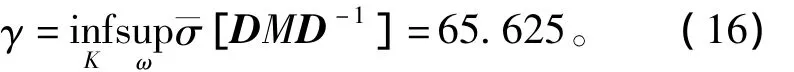
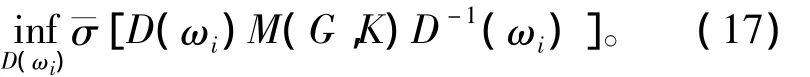
这些离散数据¯σ［D（ωi）M（G，K）D－1（ωi）］中的最大值便是这第一次迭代所得出的μ值，本例中为2.987（见表2）。

求得K后还要进行μ分析，即将K（s）代入系统中，并在各频率点上求极小，为

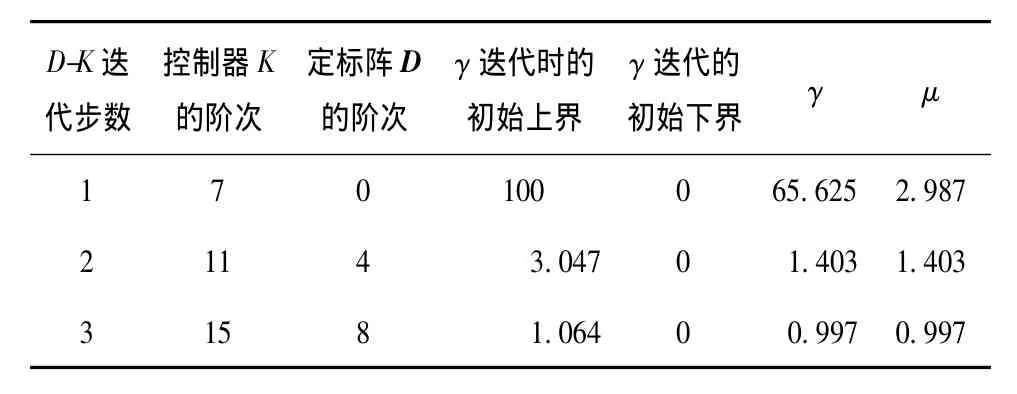
表2 迭代结果Table 2 Iteration results

第二步D-K迭代时，利用第一步所得的K（s），并对D（ωi）的数据用有理函数阵拟合得D（s），再依次求解式（16）、式（17）的优化问题，表2所示就是本例的各次迭代结果。第3次迭代后μ的最大值为0.997，就可以停止迭代了。图5所示即为3次迭代后所得的最终的控制器K奇异值bode图。

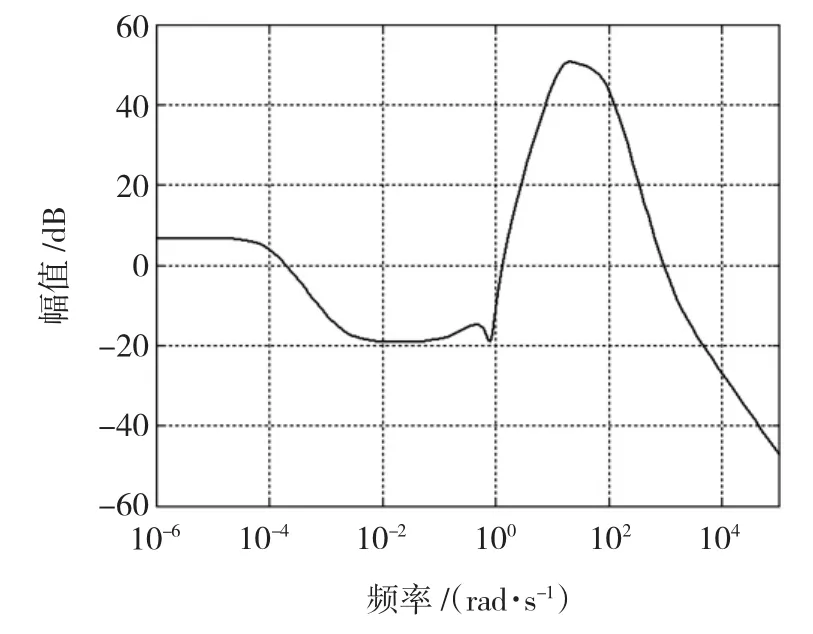
图5 三次迭代后的控制器奇异值bode图Fig．5 Bode plot of controller after 3 iterations

3 算法分析

D-K迭代实际上是一种交互式的设计过程，中间会交替出现不同的γ值和μ值，究竟哪些数据会影响到对设计过程的判断还需要分别从K和D的求解算法上来进行分析。

3.1 二分法γ迭代和γ的上界

D－K迭代中当D（ω）确定下来后就是一个H∞优化设计问题，见式（15）。H∞优化问题是指求解最小的H∞范数值γ，并给出H∞控制器K（s）。这个最小的γ值一般采用二分法来进行。即先给定一个γ值的范围，例如0～100，然后判断系统的H∞范数是否小于这个给定的上限值100。如果满足γ＜100的条件，再将这个上限折半，看是否小于50。如果不满足，则在50～100之间找。这样折半寻找，称为γ迭代，一直到满足误差要求的最小值。这里的H∞范数是否小于某个给定的γ值所依据的是H∞理论中的2个Riccati方程法，即DGKF法［7］。DGKF法指出，H∞问题是否有解（即H∞范数＜ γ）的条件是Hamilton阵H∞和J∞是否属于dom（Ric），且对应的解X∞和Y∞是否是半正定和ρ（X∞Y∞）是否小于1，式中ρ为谱半径。因此在γ迭代过程中每次都要计算H∞阵和J∞阵的特征值和广义特征向量。用计算机求解矩阵的特征值时要考虑到算法的数值稳定性问题［8］。为此在求解特征值时一般是将矩阵变换成Schur上三角形，Schur上三角形阵的对角元就是特征值。Schur变换的算法不是一种有限步的算法，而是一种迭代的QR算法［8］。QR算法是一个公认的算法，一般都可很快收敛到真实值。但若遇到病态的特征值，则会出现误差［8］。所谓病态特征值是指2个特征值非常接近的情况（例如有重根的情况）。在二分法γ迭代过程中，不断减小的γ值代入到高阶的H∞和J∞阵中难免会出现重根的情况，这时就可能会得出错误的结果。具体来说，本例中dkit是按各默认值来运行的，γmax=100，第一次的判别是γ＜100（见表1），折半后要检查是否小于50，表1第二行表明这时Y∞阵的一个最小的特征值已小于0，即Y∞已非半正定，表明系统的H∞范数不小于50，其实这是错判了。经检查，Y∞是Hamilton阵J∞的解，而γ=50时，这个J∞阵恰好存在两对重根:－1 000、－1 000和1 000、1 000。这2对病态特征值导致γ=50时迭代失败。这个判断失败，导致需要到50～100之间的二分法寻找，最终得这次γ迭代的结果是65.625。由此可见H∞优化中先后会出现2个γ值，一个是根据是否有解的条件得到的65.625，另一个则是加上控制器后实际得到的H∞范数。这前一个值可以称为是γ的上界。所以当采用dkit进行D-K迭代时，首先显示的就是γ，如果见到这么大的γ值（65.625），就可能放弃这次数据而令外寻找别的方案。其实这只是一个假象，真正的γ值并没有这么大，就本例而言，经过验证其真实值约等于第一步迭代产生的μ值，见表2的设计结果。

3.2 D拟合的收敛问题

D-K迭代中当上一步求得K（s）后，下一步就是要求解D（ω）使 ¯σ［D（ω）Fl（G，K）D－1（ω）］达到最小。这一般是在上一步先得出各离散频率点上达到极小值时的D（ωi），然后再用有理函数阵D（ω）来进行拟合，将拟合所得到的D（ω）代入式（16），再求解H∞优化问题。所以这里也有两套数据的问题，一个是逐点寻优所得的范数，另一个则是用有理函数代替后求得的H∞优化解。如果D（ω）拟合得不好，则这两套数据就会有矛盾。一般来说，D-K迭代的过程总是收敛的，但如果迭代过程中发现μ值收敛不好（有波动或变大），则很可能就是标定阵D（ω）的拟合不好。一个可能的原因是求极小值时离散点不够密，没有完全覆盖系统中的高频分量，例如弱阻尼的谐振模态。

4 结论

D-K迭代中包含γ迭代和标定阵D的求极小，在依次迭代中会出现多个范数值，弄清这些数据产生的背景，对正确进行D-K迭代是至关重要的。其实是对于γ迭代来说，因为Hamilton阵的特征值随每次的γ值而有变化，当出现病态特征值时，γ迭代过程就会停止在一个较高的虚假值上，加上控制器后的系统的H∞范数才是真正的γ值。而且这里的讨论也具有普遍意义，因为H∞控制理论中有多种方法，包括线性矩阵不等式法，这些算法得出的并不是真实的γ值，而只是一个γ的上界，加上控制器后实际得到的γ值才是真正的H∞范数。

［1］ 周克敏，DOYLE J C，GLOVER K．鲁棒与最优控制［M］．毛剑琴，钟宜生，林岩，等译．北京:国防工业出版社，2002:306－338．

［2］STEIN G，DOYLE J C．Beyond singular values and loop shapes［J］．Journal of Guidance，Control and Dynamics，1991，14（1）:5－16．

［3］LANZON A，TSIOTRAS P．A combined application of H∞loop shaping and μ-synthesis to control high-speed flywheels ［J］．IEEE Transactions on Control Systems Technology，2005，13（5）:766－777．

［4］YIN Guodong，CHEN Nan，LI Pu．Improving handling stability performance of four-wheel steering vehicle via μ-synthesis robust control［J］．IEEE Transactions on Vehicular Technology，2007，56（5）:2432－2439．

［5］BALAS G J，DOYLE J C，GLOVER K，et al．μ-Analysis and Synthesis Toolbox［M］．Natic:MathWorks and MUSYN，1993．

［6］ FRANKLIN G F，POWELL J D，EMAMI-NAEINI A．动态系统的反馈控制［M］．朱齐丹，张丽珂，原新，等译．4版．北京:电子工业出版社，2004:488－498．

［7］DOYLE J C，GLOVER K，KHARGONEKAR P P，et al．State space solutions to standard H2and H∞control problems［J］．IEEE Transactions on Automatic Control，1989，34（8）:831－847．

［8］MACIEJOWSKI J M．Multivariable Feedback Design［M］．New York:Addison-Wesley Publishing Company，1989．

（编辑:张诗阁）