基于CPSO的PID神经网络及偏航电机控制策略

朴海国， 王志新

（上海交通大学电气工程系，上海 200240）

0 引言

偏航系统作为风电机组的重要组成部分，其模型具有高度的非线性与不确定性，难以建立精确的数学模型，传统的基于精确数学模型的控制方法难于在其上取得期望的稳定性、鲁棒性等控制性能［1－2］。神经网络因具有良好的并行处理、学习、非线性映射和泛化能力［3－5］，而使其在偏航系统控制上的应用成为可能。但如何通过神经网络设计合理、简单有效、鲁棒性强的控制器，从而提高偏航控制系统在偏航过程中的稳定性、鲁棒性，进而保证系统的安全运行，成为本文关心的问题。

神经网络在控制领域实际应用的一个难点在于如何实现实时学习，从而提高系统的鲁棒性。然而，要实现给定的输入－输出映射关系，神经网络需通过训练、学习等方式确定其最优权值。但这种训练、学习过程的完成，通常需要较长时间，使得联机实时学习在实际控制中的执行遇到困难，也因此限制了神经网络在控制领域的应用。虽然为了使神经网络控制器可以进行实时学习，从而提高系统的鲁棒性，人们对提高训练收敛速度进行了不少研究，但至今仍未能有效解决此问题［6］。

粒子群（Particle swarm optimization，PSO）算法是一种新型的、基于总群进化的全局搜索算法，由Eberhart等人［7］在1995年首次提出。由于操作简单、容易执行和收敛速度快等优点，作为遗传算法等的代替算法，该算法得到了极大的发展［8］。但由于它也是基于种群的算法，因此具有其它进化算法的缺点:对初始值的敏感性和没有机制保证算法能跳出局部最优等［9］

针对以上问题，本文基于PIC/dsPIC的电动机控制和电源变换的通用开发平台UPMPC（Universal platform for motor control and power conversion）设计并搭建了小型偏航实验系统，通过实验结果与仿真结果的对比，验证了PIDNN控制策略的可行性，为改善偏航控制系统的安全运行，提高其稳定性、鲁棒性奠定了初步的实验研究基础。

1 PID神经网络与CPSO算法

1.1 PID神经网络

PID神经元网络（PIDNN）为舒怀林于1997年提出的一种新型动态神经网络［10］，其基础在于分别定义了具有比例（P）、积分（I）、微分（D）功能的神经元，从而继承了神经网络对任意函数逼近的能力，同时也拥有了PID控制具有的快速输入－输出动态特性，适合应用于复杂对象控制。其基本形式为单输出的PIDNN，采用2×3×1的3层结构形式，分别为输入层、中间隐含层与输出层，如图1所示。输入层由2个比例神经元构成，用于给定值与反馈值的输入;输出层由1个比例神经元构成，用于输出目标系统的控制量;隐含层为SPIDNN的核心结构，由P神经元、I神经元与D神经元构成，用于对输入信息的处理与变换。

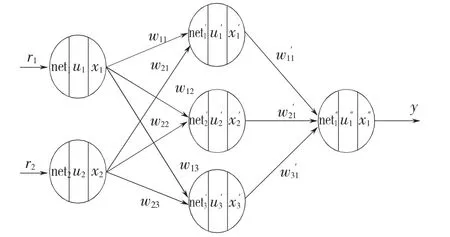
图1 SPIDNN结构拓扑图Fig．1 Topology map of SPIDNN structure

1.2 CPSO算法

为了避免早熟并保持个体的多样性从而提高系统的全局搜索能力，文献［11］提出了随机合作粒子群算法（CRPSO）。作为传统PSO粒子群的改进算法，CRPSO算法的特色在于该算法包含多个子群，通过随机方式从所有子群中选择每个子群的最优位置gbest，并用于粒子的速度与位置更新。该算法改善了传统PSO算法上的不足。但由于gbest的随机选择机制，致使各个子群的粒子更新过分依赖其他子群，从而削弱了子群自身获得的gbest在子群内部粒子更新上的作用，进而未能充分发挥子群自身的搜索能力。为克服CRPSO算法的缺陷并利用其优点，文献［12］提出了修正算法，即CPSO算法。本文采用此算法用于PIDNN控制策略的顺利完成。

CPSO算法的目标则在于充分发挥CRPSO与PSO的社会分享机制，在保持粒子个体多样性的同时，提高算法的收敛速度，从而平衡算法的全局与局部搜索能力。在CPSO算法中，通过随机方式使用其他子群最优位置gbest的同时，保留了每个子群自身最优位置gbest，每一粒子同时将两种最优位置值用于子群中粒子速度的更新。CPSO算法的更新公式为

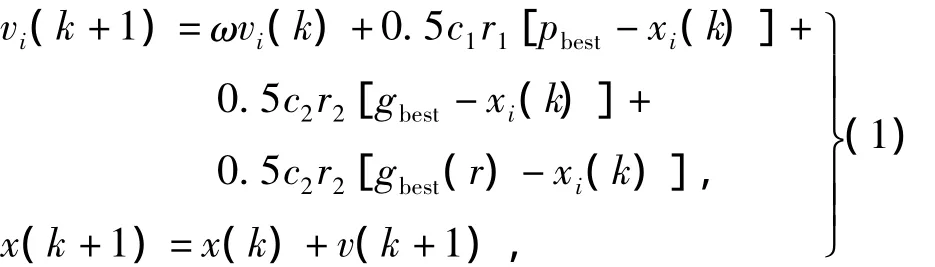
式中:v与x代表粒子的速度与位置;k为采样时刻;ω为平衡PSO算法全局搜索能力与局部搜索能力的时间衰减因子;c1与c2为正值的加速常数;r1与r2为介于0与1之间的随机数值;pbest代表粒子自身发现的最优位置;gbest为全群粒子发现的最优位置;0.5用于平衡粒子最优位置pbest，子群自身最优位置gbest与其他子群最优位置gbest（r）在更新公式中的作用;i=1，…，n，为算法中子群的数目;r为介于1到n之间的随机整数。

由公式可知，粒子的速度更新由4个部分决定，即动量部分、认知部分、内部社会部分与外部社会部分。显而易见，CPSO综合了PSO与CRPSO从而形成了一种新的信息分享机制。在粒子的进化过程中，由于更多的有用信息被使用，致使算法的全局搜索能力增强，更加容易发现全局最优值，由此，算法的鲁棒性得到加强。

2 非线性自回归滑动平均模型

NARMA模型由Leontraritis与 Billings于1985年首次提出［13］。在平衡点的邻域内，该模型可以精确描述有限维、非线性离散动态系统的输入－输出特性。偏航系统作为有限维非线性动态系统适合于使用该模型进行描述。然而，对于神经网络控制来说，该模型的非线性特性强烈地受控制输入的影响，并且对复杂的计算有较高需求，因此不适合于神经网络实现控制目的。在文献［14］中，Narendra与Mukhopadhyay提出了NARMA模型的一种近似模型——NARMA-L2模型。该模型与控制输入呈线性关系，简化了神经网络控制器的实际执行与理论分析。在本文中，基于 NARMA-L2模型，设计了PIDNN 辨识器（PIDNN Identification，PIDNNI），用于偏航电机的辨识。

2.1NARMA模型

非线性动态系统可由状态方程描述为

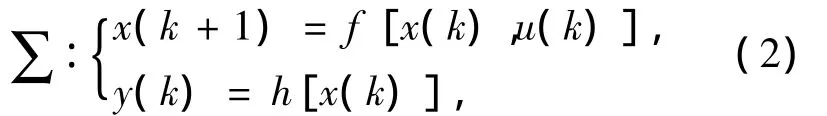
式中:u（k），x（k），y（k）分别为离散时间k时刻的输入、状态和输出值;f（·）与h（·）为映射函数。经过多步迭代计算，由状态方程（2）可得

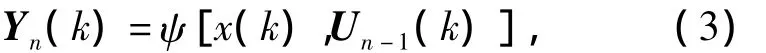
式中:Yn（k）代表序列y（k），y（k+1），…，y（k+n－1）;Un－1（k）代表序列 u（k），u（k+1），…，u（k+n －2）;ψ（·）为映射函数。对于式（3）模型，使用神经网络辨识的表达式可表示为

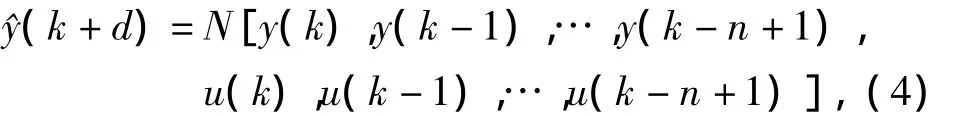
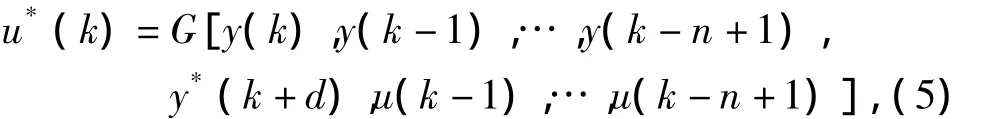
式中:u*（k）为神经网络在k时刻的期望控制输出;G（·）为网络映射。由式（4）、（5）比较可知，需要另外的神经网络参与，从而顺利完成N（·）到G（·）控制器的设计;因此，基于NARMA模型设计的神经网络控制器增加了计算量的同时也增加了控制器设计的复杂性。

2.2 NARMA-L2模型

NARMA-L2为NARMA模型围绕标量u（k）而有的泰勒展开式。当输入u足够小时，余量R可忽略不计，即通过降低输入u的幅值，NARMA-L2模型可以达到任意期望的精度。NARMA-L2模型的表达式为

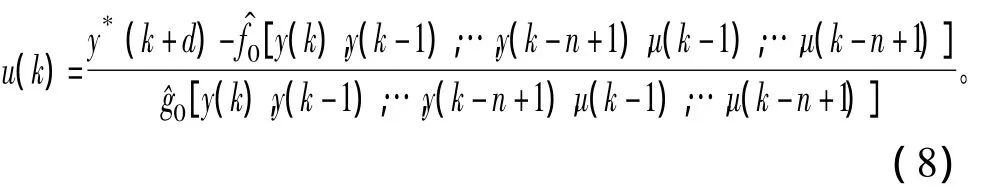
比较式（5）与式（8）可知，控制器的设计变得相对简单，仅通过代数变化方式便可得到期望的控制输出u（k）。

3 PIDNNC-I合成控制系统设计

3.1 PIDNNC-I控制系统

PIDNNC-I控制系统简化框图如图2所示。本文采用矢量控制技术用于完成对偏航电机的主电路供电控制。矢量控制技术为普遍应用于三相感应电机上的常用控制技术，其本质上为一种稳态解耦控制，只有当转子磁链达到稳态并保持恒定时，才能实现转速与转子磁链之间的解耦，而不能实现转速与转子磁链的动态解耦。不但如此，由于该技术为基于感应电机数学模型的一种控制技术，导致控制系统的参数鲁棒性与抗负载扰动能力差。本小节将偏航电机与矢量控制部分以及三相逆变附加电路视为一整体被控对象而加以控制。由磁链控制对速度控制造成的不利影响可视为一种不确定扰动，并由PIDNNC-I速度控制器加以抑制。

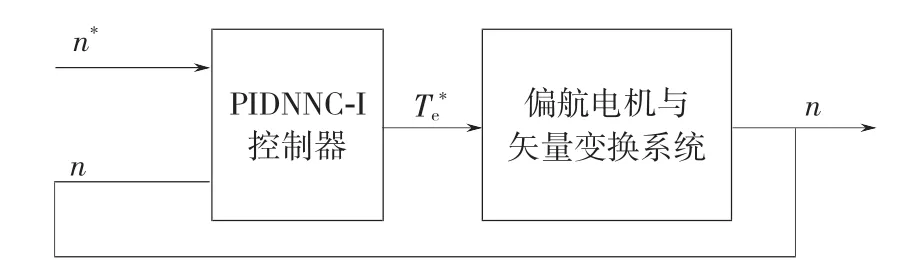
图2 PIDNNC-I控制系统简化框图Fig．2 Simplifying block diagram of PIDNNC-I control system

3.2 PIDNNC-I控制器

PIDNNC-I控制器由2部分构成，PIDNNC控制器与I积分控制器，2部分共同作用给出期望的控制输出。PIDNNC控制器基于NARMA-L2模型，由PIDNNI辨识器设计与PIDNNC实现两个阶段完成。

3.2.1 PIDNNI辨识器设计

PIDNN辨识器的设计用于完成NARMA-L2模型映射函数f0（·）与g0（·）的辨识。辨识所得结果即为所需的网络映射0（·）与0（·）。基于 PIDNN设计的辨识器结构简图如图3所示，其中ui与xi（i=1，2）分别为输入层第i个神经元的状态与输出值;上角标“'”为隐含层变量标记;1，2，3为隐含层神经元序号;wsij为输入层与隐含层之间的连接权重变量，s=1，2为SPIDNN神经网络个数，i=1，2为输出入层神经元序号，j=1，2，3为中间隐含层神经元序号）;上角标“″”为输出层变量标记;wsjh为隐含层与输出层之间的连接权重变量，h=1，…，m，为输出神经元数目，这里h=1。

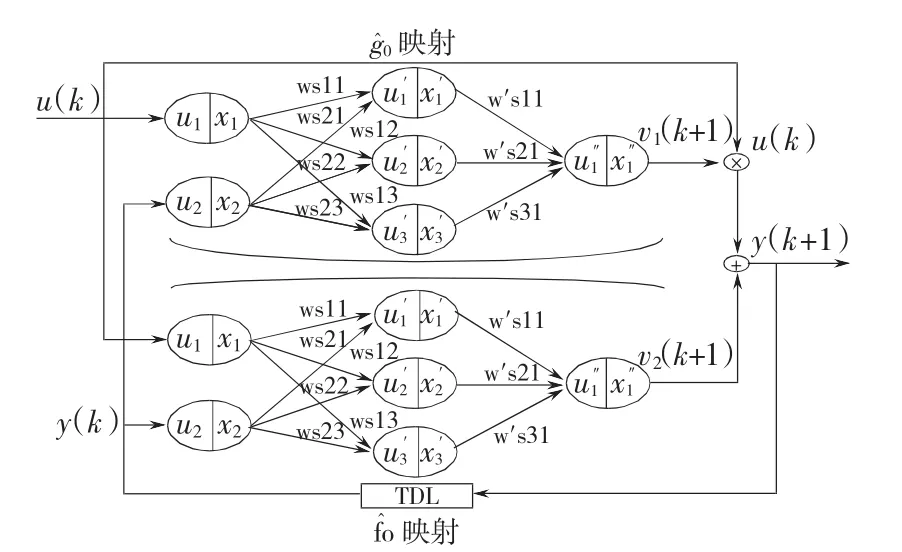
图3 PIDNNI辨识器模型结构简图Fig．3 Identifying model structure of PIDNNI

3.2.2 PIDNNC控制器设计

根据NARMA-L2模型的原理可知，经过PIDNNI辨识后，通过代数变换即可获取所需控制器模型。PIDNNC控制器模型结构图如图4所示，其中s为子网序号，在0（·）与0（·）中分别为 1，2;K1，K2，K3与K4分别为变换系数，用于输入－输出数值的比例变换。

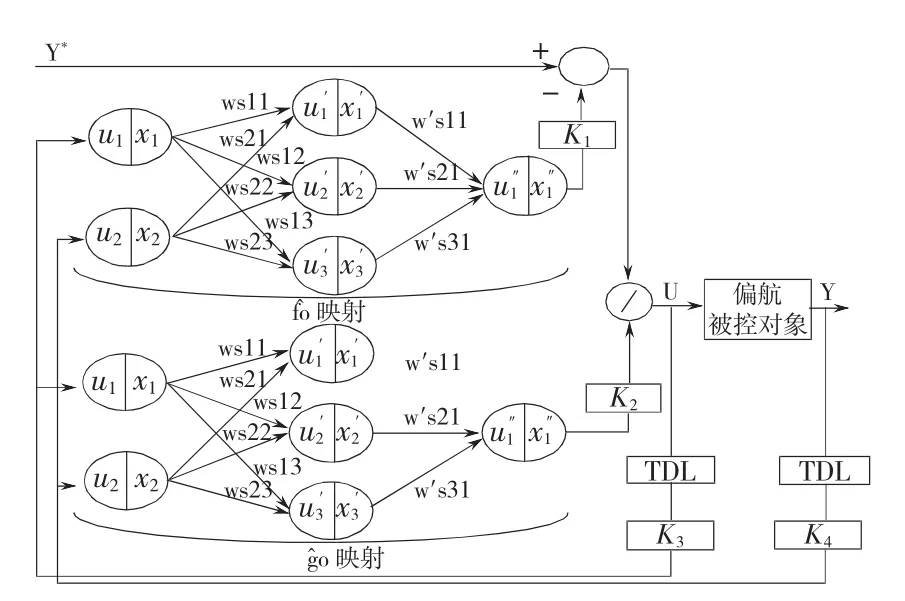
图4 PIDNNC控制器模型结构图Fig．4 Controller model structure of PIDNNC

3.2.3 积分控制器设计

作为动态神经网络，基于CPSO算法的PIDNNI辨识模型能有效减小辨识误差，提高对真实系统的近似程度，但这并不意味它能完全取消系统辨识误差，即PIDNNC的控制输出与期望输出总会有些许偏离。为进一步提高控制鲁棒性与控制精度，基于系统辨识误差的不可取消性，本文给出了PIDNNC-I合成控制策略，即在大跟踪误差范围内，采用PIDNNC控制;在小跟踪误差范围内，采用PIDNNC与积分的联合控制。为避免积分过饱和，速度偏差e的范围给定不应太大;同时，为防止积分不足，速度偏差e的范围又不能太小。本章选取的积分范围为［－10，10］，为加速积分过程，选取的积分系数为3 000。

为加快辨识模型的收敛速度，统一输入与输出量的单位不同，本文对辨识模型所用训练数据进行了归一化处理。为不影响控制模型的控制效果，在控制过程中采用了与辨识相对应的论域变化，其变换公式为

式中:xmax与xmin为输入或输出的上限与下限;x为实际输入或输出值;x*为输入或输出的变换值。在图 4 中，K1=K2;K3=K4。

4 仿真试验

本节将对负载波动、转速波动进行仿真方式，以验证所提控制策略的有效性，并根据所得结果做出分析与总结。

4.1 辨识和控制系统参数给定

将5kW三相异步感应电机作为偏航电机用于本仿真研究，其参数如表1所示。基于CPSO算法的PIDNNI辨识模型及训练参数如表2所示。根据网络的层次不同，权值空间由2部分构成，即输入层至隐含层的权值解空间和隐含层至输出层的权值解空间。基于网络层次的不同，算法的搜索范围与搜索速度也可分为2部分而进行分别设定。

表1 偏航电机参数Table 1 Parameters of a yaw motor

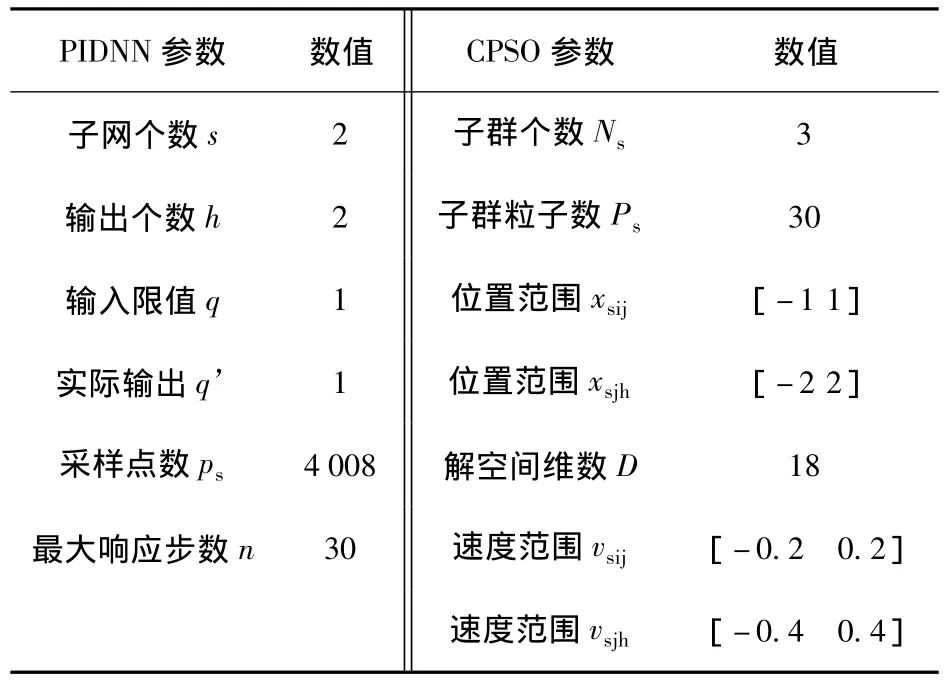
表2 PIDNNI辨识模型与CPSO算法参数Table 2 Parameters of PIDNNI and CPSO

4.2 系统辨识

辨识数据来源于被控对象的随机输入与相应的输出。数据曲线如图5所示，其中，图5（a）中给出了电磁转矩的随机输入曲线;图5（b）、（c）为相应的辨识结果与辨识误差曲线。观察图5可知，辨识曲线与目标曲线几乎完全重合，在30步的训练下，辨识误差值收敛到3.578 72×10－7，表明本章所提辨识模型能有效辨识被控对象，并取得非常高的辨识精度;同时表明CPSO算法具有强劲的搜索能力，能较早发现全局最优解而提高了算法的收敛速度。

4.3 速度恒定时的负载波动

初始条件:参考速度给定，n*=400 r/min;负载转矩 TL=30 N·m。在转矩变化下，为验证PIDNNC-I控制系统的控制性能，在0.16，0.24和0.34 s时刻，不同负载将加载于被控对象。作为对比参考，基于PID控制器的控制结果将用来与本文所提控制器的控制结果进行比较。基于变化负载的速度与转矩仿真曲线如图6所示。

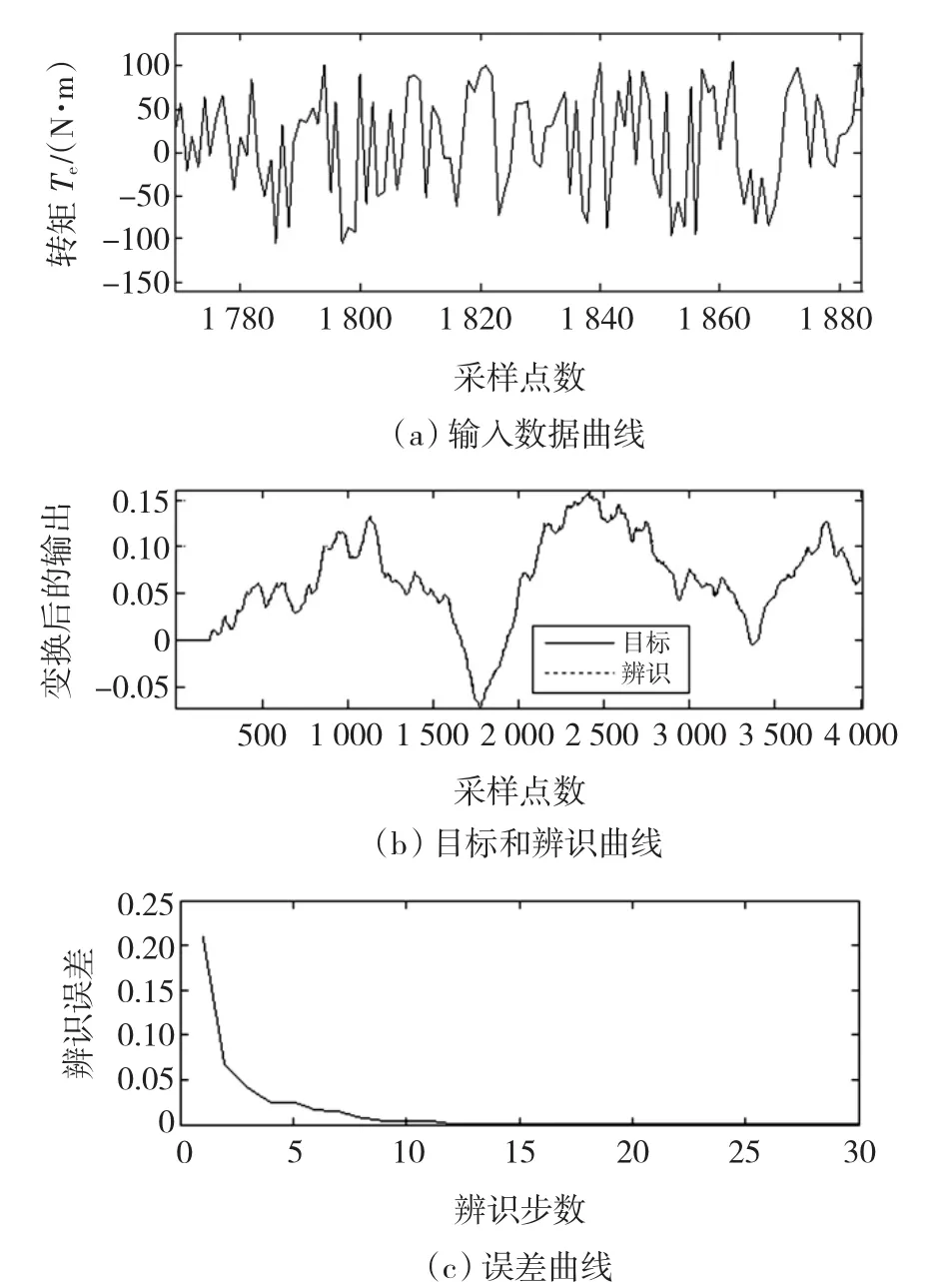
图5 辨识数据与辨识结果图Fig．5 Data and results of identifying

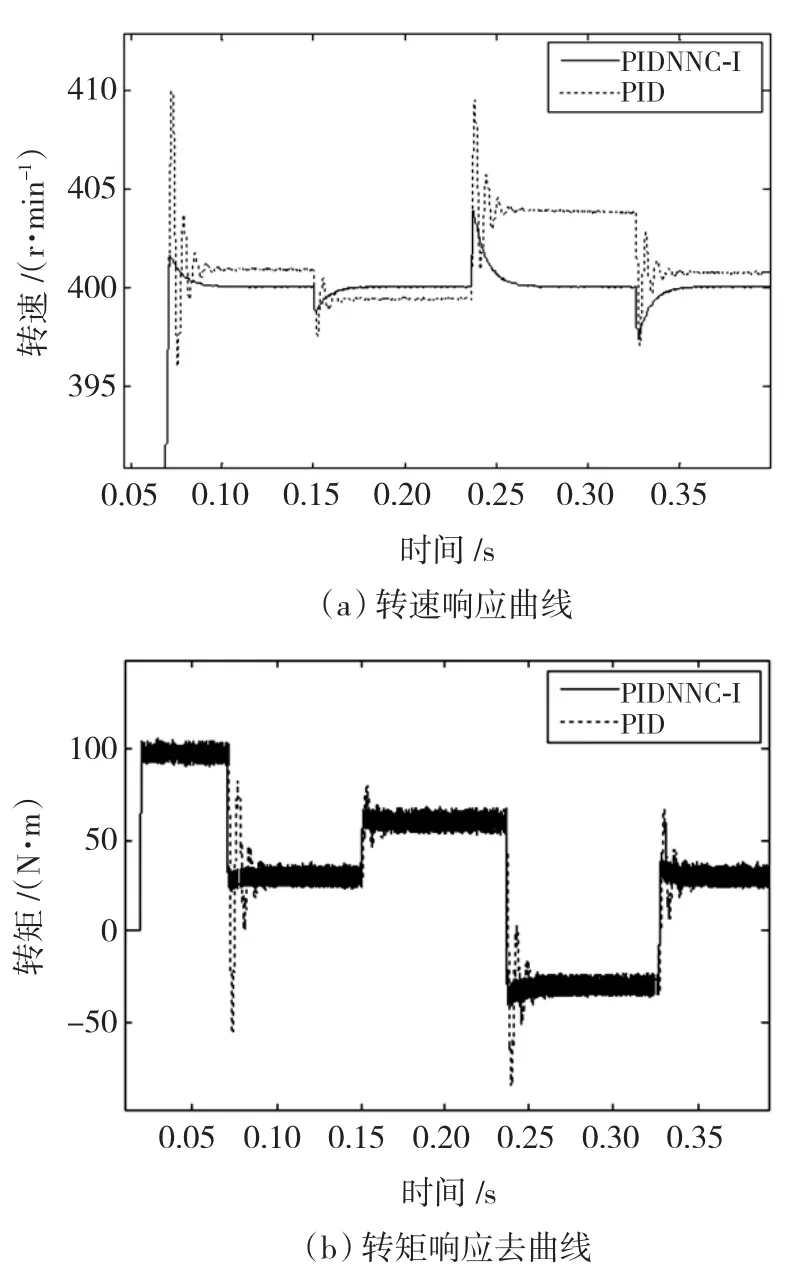
图6 负载波动下的转速与转矩响应曲线Fig．6 Curves of speed and torque with change of load

在升速阶段，PIDNNC控制器将会单独起作用，直至速度偏差减小到15 r/min，此时，积分控制器有效，同PIDNNC共同给出期望的控制输入。由图6可以观察到，PID控制器引起速度、转矩大的调节振荡，最大超调量超过2.5%，同时使系统拥有稳态误差。与此相反，PIDNNC-I控制器没有发生超调振荡，无稳态误差问题，其最大超调量仅为0.375%。

在0.16 s时刻，负载转矩TL由30 N·m变化到60 N·m。由图6（a）可知，PID控制器的稳态误差也发生了变化，即稳态误差值由正变负。与PID控制器相比，PIDNNC-I控制器拥有更好的控制性能表现，没有引起超调振荡，同时，稳态误差仍然保持为零值。

在0.24 s时刻，负载突然由60 N·m减小为－30 N·m。该变化导致偏航电机出现快速加速过程。PID与PIDNNC-I控制器两者均快速做出反应，使电磁转矩T*

e由正变负，以便抑制速度发生变化。对比响应曲线可知，PIDNNC-I控制器的反应速度较之PID控制器灵敏;因此，在速度偏差增大到4 r/min前就开始回落，没有出现超调振荡，稳态误差仍然保持为零值。反之，PID控制器的控制情形有很大不同，出现了强烈的超调振荡过程，同时，稳态误差变大。

在0.34 s时刻，负载由－30 N·m变化到30 N·m，响应与分析与0.16 s时刻相类似。

由以上分析可知，对于负载波动，PIDNNC-I控制系统具有更好的动、静态响应性能，即降低了超调量，未出现振荡调节，稳态维持保持为零值。

4.4 负载恒定时的速度波动

为看清系统的响应变化过程，选择的参考转速分别为400，350，450 r/min。在最后一次参考转速给定的同时，负载转矩由30 N·m变化到－30 N·m。仿真曲线如图7所示。

由图7可知，随着参考转速的变化，PID控制系统出现了强烈的转速与转矩振荡调节，与负载转矩波动实验相比，其最大超调量有所增加，而PIDNNC-I控制效果与PID控制形成鲜明对比。由于PIDNNC-I具有更快的反应速度，更优良的动、静态响应性能，因而并未出现强烈的转速、转矩振荡调节过程，其静态跟踪误差为零值。图7再次表明，基于PIDNNC-I的控制增加了系统的鲁棒性与稳定性。图7（c）为转速、转矩在参考转速为350 r/min时的局部放大图。该图有利于更加清晰的看清响应曲线，并给出更多响应过程的细节描述。

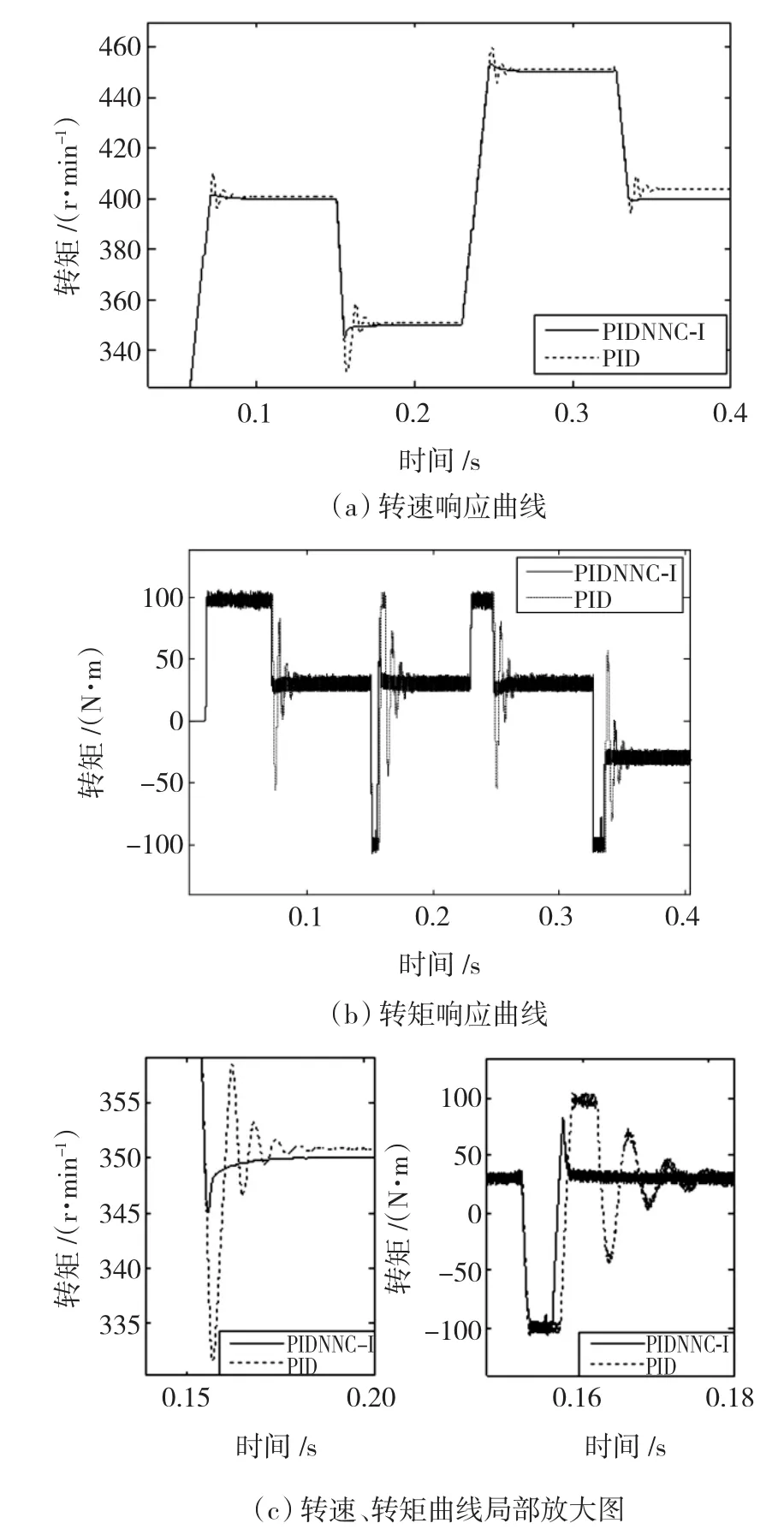
图7 转速波动下的转速、转矩响应曲线Fig．7 Responding curves of speed and torque with change of speed

5 试验研究

为定量验证所提控制策略的正确性，基于PIC/dsPIC的电动机控制和电源变换的通用开发平台UPMPC设计并搭建了小型偏航控制试验验证系统。

5.1 辨识和控制系统参数给定

将0.25 kW Leeson三相异步感应电机作为偏航电机用于本实验研究，其参数见表3。

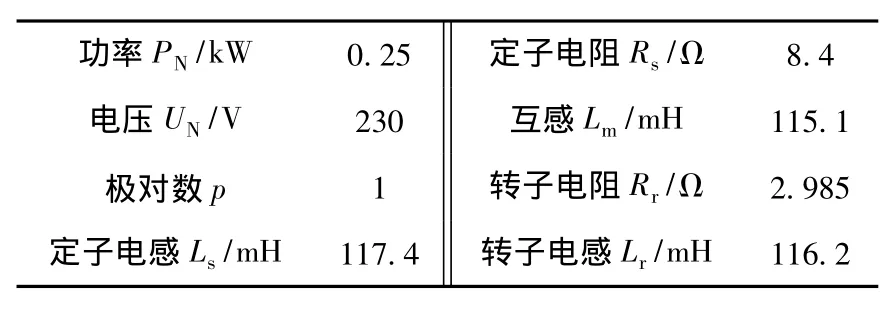
表3 偏航电机参数Table 3 Parameters of 0.25 kW yaw motor

基于CPSO算法的PIDNNI辨识模型及训练参数见表4。

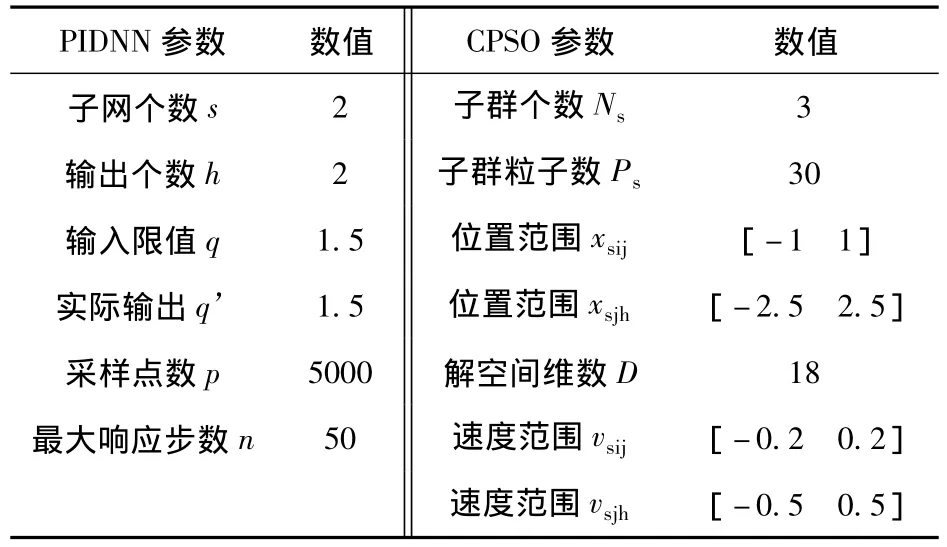
表4 PIDNNI辨识模型与CPSO算法参数Table 4 Parameters of PIDNNI and CPSO

5.2 实验系统辨识

在本实验中，被控制对象的随机输入由MATLAB随机函数根据电机的转矩范围随机给出，并通过编程方式设定电磁转矩给定值。在每给定一随机电磁转矩的同时，在下一指令周期便开始对速度估计值进行存储，从而构成数据对用于系统的辨识。系统的辨识过程由编写的MATLAB M文件完成。数据曲线如图8所示。

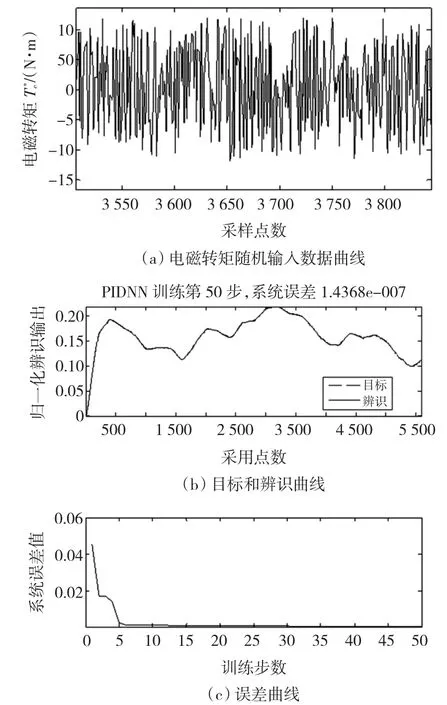
图8 辨识数据与辨识结果图Fig．8 Data and results of identifying

图8（a）给出了电磁转矩的随机输入曲线，图8（b）、（c）为相应的辨识结果与辨识误差曲线。观察图8可知，辨识曲线与目标曲线几乎完全重合，在50步的训练下，辨识误差值收敛到1.436 8×10－7，表明PIDNNI辨识器模型在适当修改辨识参数后，能有效辨识本章所设计的偏航实验控制系统。辨识所得最优权值如表5所示。

表5 最优权值Table 5 Optimal values of weight

5.3 速度恒定时的负载波动

初始条件:参考速度给定，n*=500 r/min;负载转矩TL=2 N·m。在两个不同的采样点时刻，不同负载将加载于被控对象。基于变化负载的速度与转矩实验曲线如图9所示。在采样点2058处，负载转矩TL由2 N·m变化到9 N·m。由图9（a）可知，稳态误差仍然保持在零值附近。在采样点3900处，负载突然由9 N·m减小为5 N·m，该变化导致偏航电机出现快速加速过程，引起较小的超调振荡。实验结果与仿真结果相近，表明了PIDNNC-I控制策略是正确可行的。

5.4 负载恒定时的速度波动

初始条件:参考速度给定n*=500 r/min，负载转矩TL=2 N·m。在两个不同的采样点时刻，n*分别为460，540 r/min用作于系统参考速度。实验曲线如图10所示，实验结果与仿真结果相近。由于PIDNNC-I控制器具有较快的反应速度，随着参考转速的变化，虽然实际转速有震荡调节过程，但并不十分强烈，其静态跟踪误差为接近零值。

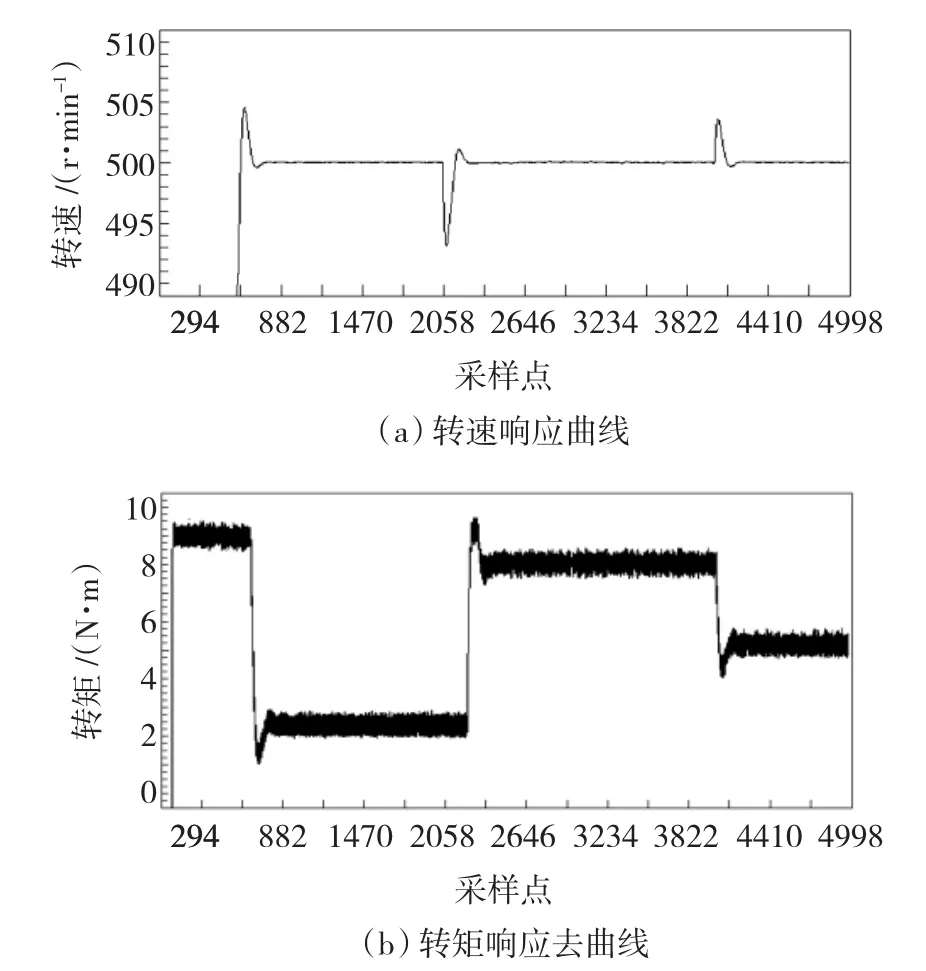
图9 负载波动下的转速与转矩响应曲线Fig．9 Curves of speed and torque with change of load

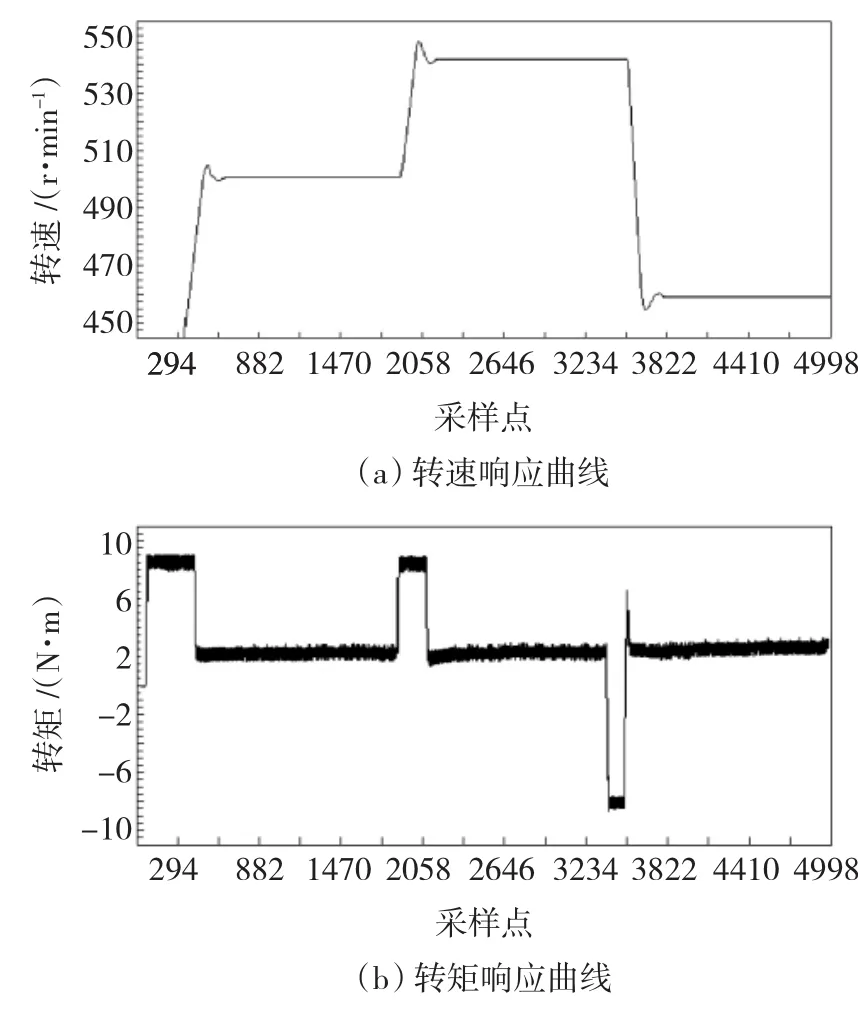
图10 转速波动下的转速和转矩响应曲线Fig．10 Responding curves of speed and torque with change of speed

6 结论

作为复杂非线性动态系统，偏航系统控制难于获取高精度控制性能。借鉴传统静态神经网络的逆系统控制方法，本文给出了基于CPSO合作粒子群算法的PID神经网络控制策略，通过建立偏航系统的仿真模型，进行仿真实验，并与PID控制器的控制效果进行比较，表明该控制策略在提高偏航系统的稳定性、鲁棒性与控制精度上的有效性，有利于PIDNN在控制领域的广泛应用。同时，对小型PIDNNC-I偏航控制系统进行的转矩、转速实验研究表明了该控制策略的可行性，对偏航系统的安全运行与系统寿命的提高具有参考、借鉴意义。该实验系统以及所提出的控制策略也适合应用于其他非线性动态系统，并可期望获得较高精度的控制性能。

［1］朴海国，王志新．风电机组偏航控制系统的新型算法——VHC研究［J］．太阳能学报，2008，29（8）:1028－1033．

PIAO Haiguo，WANG Zhixin．A new control algorithm for yaw control system of wind turbine［J］．Acta Energiae Solaris Sinica，2008，29（8）:1028－1033．

［2］朴海国，王志新．风电机组智能模糊偏航矢量控制系统研究［J］．太阳能学报，2009，30（4）:481－487．

PIAO Haiguo，WANG Zhixin．Study of intelligence fuzzy yaw vector control system of system of wind turbine［J］．Acta Energiae Solaris Sinica，2009，30（4）:481－487．

［3］张代远．神经网络新方法［M］．北京:清华大学出版社，2006:1－11．

［4］ 杨建刚．人工神经网络实用教程［M］．杭州:浙江大学出版社，2001:1－8．

［5］ 周开利，康耀红．神经网络模型及其MATLAB仿真程序设计［M］．北京:清华大学出版社，2005:1－7．

［6］戴先中．多变量非线性的神经网络逆控制方法［M］．北京:科学出版社，2005:1－20．

［7］KENNEDY J，EBERHART R C．Particle swarm optimization［C］//Proceedings of IEEE International Conference on Neural Networks．Perth，Australia:IEEE Press，1995:1942 －1948．

［8］SONG Y，CHEN Z Q，YUAN Z Z．New chaotic PSO-based neural network predictive control for nonlinear process［J］．IEEE Transations on Neural Networks，2007，18（2）:595－601．

［9］SHI Y，EBERHART R C．A modified particle swarm optimizer［C］∥Proceedings of the IEEE Congress on Evolutionary Computation．Piscataway:IEEE Press，1998:69 －73．

［10］SHU Huailin．Study on the neural PID network cascade control system［J］．Automation＆Instrumentation，1997（5）:5－7．

［11］ZHAO L，YANG Y．PSO-based single multiplicative neuron model for time series prediction［J］．Expert Systems with Applications，2009，36（2）:2805 －2812．

［12］PIAO H，WANG Z，ZHANG H．Cooperative-PSO-based new learning algorithm for PID neural network and nonlinear control design［J］．The Mediterranean Journal of Measurement and Control，2009，5（2）:60 －70．

［13］LEONTARITIS I J，BILLINGS S A．Input-output parametric models for nonlinear systems（Part I）:deterministic nonlinear systems［J］．Int．J．Contr．，1985，4（2）:303 －328．

［14］NARENDRA K S，MUKHOPADHYAY S．Adaptive control using neural networks and approximate models［J］．IEEE Transactions on Neural Networks，1997，8（3）:475 －485．

（编辑:张静）