提高卫星姿态机动性能的后步法与LPV控制
2010-02-10曾鸣王佳
曾鸣, 王佳
(哈尔滨工业大学空间控制与惯性技术中心,黑龙江哈尔滨 150001)
0 引言
现代的卫星经常需要进行快速大角度姿态机动来执行各种任务,由于角速度耦合交叉项的存在,这些快速姿态机动问题经常被归结为非线性刚体动力学问题。过去的十多年当中,滑模控制[1]、线性H∞控制[2]和逆最优[3]等各种控制策略均被应用卫星姿态控制当中。近年来,后步法设计控制器策略[4]被应用到卫星姿态控制当中,这种控制器设计方法适用于各种级连系统,姿态控制系统即由动力学到子系统与运动学子系统组成的级连系统[5]。后步控制策略的递归设计步骤可解决非线性系统的控制问题,其解决全局稳定性问题的优点被广泛采纳,但存在的问题是不能保证某个输出信号具有良好的暂态性能。
增益调度是一种很好的非线性控制器设计方法,且已被广泛用于机器人控制和卫星控制当中[6],增益调度设计方法能保证系统在某一操作空间内满足性能指标的要求。基于增益调度设计方法的这一优点,一种被称为线性参数可变(LPV)的增益调度系统化设计方法被研究人员广泛关注[7],该方法不仅设计方法系统化,而且能满足稳定性和保性能两方面的设计要求。LPV控制器设计理论能简化常规的增益调度设计方法中的插值与实现问题;然而,LPV系统所满足的的稳定性和保性能要求只局限于某一局部操作空间内。
近来一种用于提高非线性系统性能的混合控制策略被提出[8],这种混合控制策略分别应用后步法和LPV控制的优点来弥补对方的不足,在保证非线性系统的全局稳定性的前题下,提高系统的局部性能。
本文将上述由后步法与LPV法设计的混合控制器首次应用到卫星姿态控制当中,设计的控制器既能保证系统的全局稳定性,又能提高系统的干扰抑制能力并改善系统的暂态响应性能。采用的平方和(SOS)数值计算方法弥补了文献[7]中LPV控制器的求解不能得到全局解的不足。
1 卫星姿态运动模型
刚体卫星姿态动力学模型[5]为




式(8)为LPV形式的卫星姿态运动模型,则基于后步法和LPV法的混合控制在卫星姿态控制中应用问题可表述为:在平衡点以外的大部分轨迹空间内采用以模型(2)和(4)为基础设计的后步控制器,当系统的状态进入到平衡点附近的指定区间后,系统则采用以式(8)为基础设计的LPV控制器来提高系统的局部性能,本文的性能提高是指从干扰到输出的诱导L2范数小于某一预先给定值的暂态性能提高。
2 SOS分解与Lyapunov设计方法
一个多变量多项式f(x1, …, xn)是SOS,当存在一组多项式f1(x),…,fm(x)满足
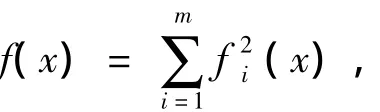
满足上式条件的f(x1, …, xn)必然是非负的;因此,SOS分解为变量多项式非负定提供了充分条件,且等价与
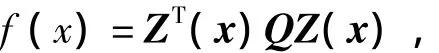
式中:Q为一半正定矩阵;Z(x)为某一单项式向量。判断一个多变量多项式为SOS比正定更容易计算,且用SOS代替非负定得到的计算结果更加精确[11]。
以下介绍基于SOS工具和Lyapunov方法的控制器设计过程。首先为了设计控制器,选定Lyapunov函数

这里 P >0;因此,V(x)>0。
沿状态空间方程对Lyapunov函数微分,得

若将式(10)代入式(8)所得闭环系统为渐近稳定,则多项式<0。而判断一个多项式是非负定问题是一个NP难题。采用SOS判断多项式的非负定就很容易[9]。
若式(12)改为SOS约束条件,则使系统稳定的控制器设计问题可表述如下。
定义1 设计 P,K(x),ε(x),使得
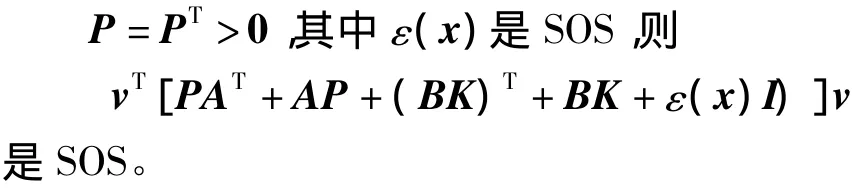
传统的LPV控制器设计最终都归结为解一个参数依赖的线性矩阵不等式(PLMI)问题,而一般的数值仿真求解得到的均为参数可变线性矩阵不等式的局部解。若采用SOS方法来代替求解参数依赖的线性矩阵不等式的方法,可以得到全局解[10]。本文采用SOS方法来求解控制器。
3 基于后步法与LPV的混合控制器设计
为了提高系统的暂态响应性能,设计一种混合控制方法。首先采用后步法设计控制器将系统的初始状态驱使进系统平衡点的某一邻域内,然后切换到LPV控制器上来改善系统的局部暂态响应性能。
3.1 后步姿态控制器设计
对于式(2)和式(4)表示的卫星姿态控制系统,假设qd(t)为期望姿态轨迹,定义qe≜q-qd为每一时刻的姿态四元数误差,为了便于控制器的设计,这里重新定义新的变量,即


这里转动惯量矩阵J被包含在系统动力学方程中,为将J分离出来,引入线性算子



3.2 应用LPV控制器提高局部性能指标
为了提高系统的暂态响应性能,设计一种混合控制方法。首先采用后步法设计的控制器将系统初始状态驱使进平衡点的某一邻域内,然后切换到LPV控制器上来改善系统的局部性能。
为了提高局部的暂态响应性能指标,首先需明确局部区域的范围。选择如下的椭球区作为LPV控制器的工作空间,即

以下称式(22)所表示的集合为LPV控制器的工作区间。
对于式(8)用LPV形式表述的卫星姿态控制问题,设计目标是找到一个状态反馈控制器 u=K(x)x,使得闭环系统为渐近稳定的,且从d到y的诱导L2范数小于γ。
定理2 对于系统(8)若存在一个对称矩阵Pl(x)和一个常数 ε1>0,以及一个 SOS ε2>0,使得下列表达式均为SOS,即



定理1的证明过程参考文献[11]。
4 仿真分析
以下实例用来验证上述设计理论的可行性。仿真目标是把初始姿态为零的刚体卫星机动至某一给定姿态。这里选择的刚体卫星的转动惯量为
I=diag(300,320,250)(kg·m2)。初始角速度为零,初始姿态的欧拉角为 θ1=(0°,0°,0°),目标姿态的欧拉角为 θ0=(75°,-175°,70°);初始姿态的四元数为(0,0,0;1),目标姿态的四元数为(0.6401,0.0614,0.0054;-0.7658),把初始数据代入式(13a)~(13c)中,给定姿态控制系统受到外部常值干扰为[1 1 1]T×10-3(N·m),对于式(19)表示的后步控制器选择的增益为k1=1,k2=0.1,k3=0.02,对于式(20)的自适应律,选取
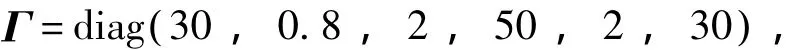

则式(19)表示的后步控制器为将初始数据代入式(8)中,选取定理1中的γ为4。应用参考文献[9]中的软件包SOStools求解出的LPV控制器为

仿真结果图1为单独应用后步法设计控制器的姿态控制系统在控制力矩存在干扰时,用四元数描述的姿态角的变化,计算出的从干扰d到姿态角输出y的诱导L2范数为17.35。图2为角速度的变化曲线。
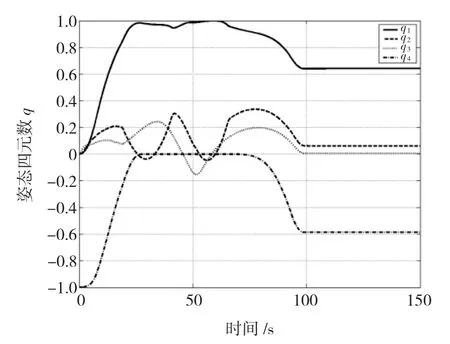
图1 应用后步控制器姿态四元数变化曲线Fig.1 Time history of attitude quaternion with back-stepping controller
仿真结果图3为应用混合控制器的姿态控制系统在控制力矩存在相同干扰时,用四元数描述的姿态角的变化,计算出的从干扰d到姿态角输出y的诱导L2范数为3.7。图4为角速度的变化曲线。
应用混合控制策略的闭环系统不仅保证了系统的全局稳定性,关键是在系统状态进入到稳定工作区后,系统的干扰抑制能力得到了提高,闭环系统从d到y的诱导L2范数不仅满足了γ<4的要求,而且要远小于单独使用后步法设计的控制器时此项指标值。

图2 应用后步控制器角速度变化曲线Fig.2 Time history of angular velocity with back-stepping controller

图3 应用混合控制器姿态四元数变化曲线Fig.3 Time history of attitude quaternion with hybrid controller
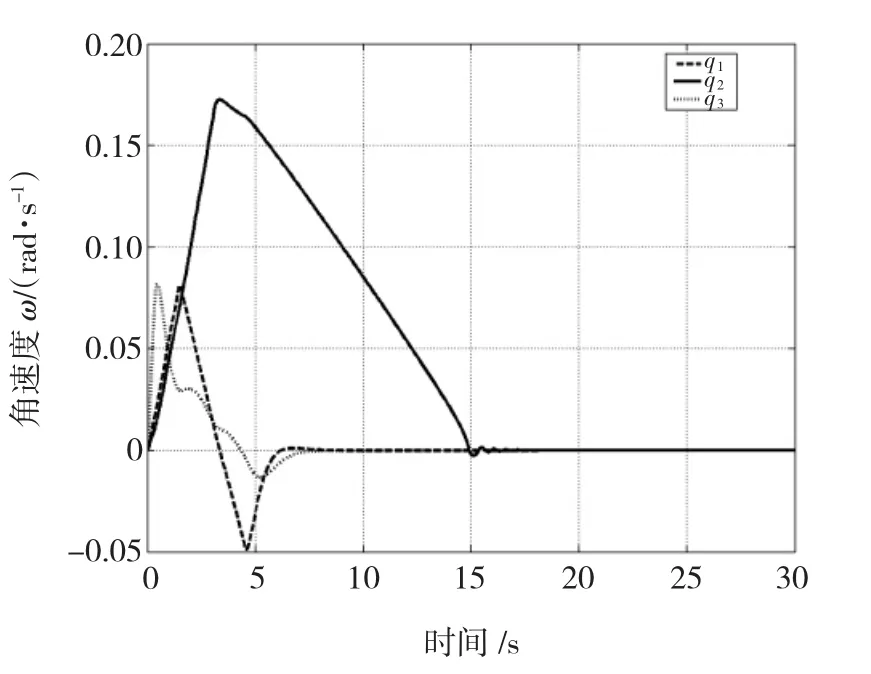
图4 应用混合控制器角速度变化曲线Fig.4 Time history of angular velocity with hybrid controller
5 结论
提出了一种混合控制策略用于提高卫星姿态控制的性能指标。首先,用后步法设计控制器来保证卫星姿态机动过程系统全局鲁棒稳定性,然后,应用基于LPV的非线性H∞控制策略来提高系统的局部性能。在系统平衡点以外的大部分空间内使用后步法控制策来保证系统的稳定性,当系统的状态轨迹进入到平衡点附近区域后则将非线性的系统视为LPV系统,进而采用基于LPV的非线性H∞控制策略来提高系统的干扰抑制能力。仿真结果表明,应用混合控制策略既能保证系统全局稳定,又能提高系统的干扰抑制能力和改善暂态性能,从而避免了使用后步法造成系统性能差,使用LPV控制不能保证系统全局稳定的不足。后续的工作可以将此方法应用到挠性飞行器控制中。
[1]CHEN Y P,CLUO S.Sliding-mode controller design for spacecraft attitude tracking maneuvers space [J].IEEE Trans.Aero.Electro.Sys.,1993,29(3):1328 -1333.
[2]SKULLESTAD A,GILBERT J M.H∞control of a gravity gradient stabilized satellite [J].Control Engineering Practice,2000,8(2):975-983.
[3]SHARMA R,TEWARI A.Optimal nonlinear tracking of spacecraft attitude maneuvers[J].IEEE Trans.Contr.Sys.Tech.,2004,12(5):677-682.
[4]KIM K S,KIM Y,Robust back-stepping control for slew maneuver using nonlinear tracking function [J].IEEE Trans.Contr.Sys.Tech.,2005,12(7):907 -912.
[5]TSIOTRAS P,Stabilization and optimality results for the attitude control problem[J].J.Guidance,Contr.Dyn.,1996,19(9):772-779.
[6]RUGH W J,SHAMMA J S.Research on gain scheduling[J].Automatic,2000,36(10):1401-1425.
[7]WU F,YANG X H,PACKARD A,et al.InducedL2norm control for LPV systems with bounded parameter variation rates[J].Int.J.Robust Non.Contr.,2005,6(9/10):983 -998.
[8]ZHENG Q,WU F.Improving nonlinear control performance with a hybrid control strategy[C]∥Proc.46th IEEE Conf.on Dec.and Contr.,Dec..Los Angeles,America:IEEE,2007:3208 -3213.
[9]BILIMORIA K D,WIE B.Time-optimal three-axis reorientation of a rigid spacecraft[J].Journal of Guidance,Control,and Dynamics,1993,16(3):446 -452.
[10]PARRILO P A.Structured Semi Definite Programs and Semi Algebraic Geometry Methods in Robustness and Optimization[D].California:California Institute of Technology,2000.
[11]WANG J,ZENG M.Nonlinear H∞control of large angle attitude maneuvers for satellite using sum of squares[C]∥IEEE International Conference on Mechatronic and Automation.Changchun,China:IEEE,2009:358-363.
(编辑:张静)
