多相集中整距绕组感应电机的建模与仿真
2010-02-10张经纬祝后权黄振华杨高戴勇
张经纬, 祝后权, 黄振华, 杨高, 戴勇
(中船重工集团第七一二研究所,湖北武汉 430064)
0 引言
在变频传动系统中,采用多相感应电机可以降低定子相电流,实现电机的低压大容量设计,避免功率器件的串并联以及由此带来的均流问题。此外,多相电机具有空间谐波含量少,转矩脉动小,可靠性高,控制方式多样化等优点,因此在国防军工等其他要求高可靠性、大功率的领域内得到广泛的应用[1]。为了提高多相电机传动系统的整体性能,考虑到变频装置供电方式的灵活性,人们设法通过对变频装置和多相电机的匹配设计,使得整个系统获得最佳的运行性能。H.A.Toliyat等人[2-3]从电机设计的角度分析认为,如果将多相电机的定子绕组设计为集中整距绕组以适应逆变器输出的方波电压(或电流),此时整个系统的性能最佳。R.O.C.Lyra等人[4]通过在双Y移30°六相感应电机的外加电压中注入三次谐波,在保证气隙磁密幅值不变的基础上提高基波电压的幅值,使得电机的转矩密度大幅提高。
采用集中整距绕组和非正弦供电是提高多相感应电机功率密度的重要途径,为分析上述措施对电机性能的影响,同时开展变频装置与电机的匹配性研究,需要建立比较客观准确的机电动力系统模型,而传统的基于d-q-n坐标变换的异步感应电机建模方法[5]则存在一定的局限性,主要是因为:①传统的建模方法仅仅考虑基波,将谐波的影响作为漏抗处理,而在多相整距绕组感应电机中,如果谐波电流产生的空间磁势与基波具有相同的转速,那么谐波也会产生有效的力矩作用,因此不能将谐波作为漏抗处理;②传统的建模方法将转子导条等效为正弦分布的三相绕组,在此基础上推导定转子之间的互感参数,从而简化分析与计算;而在m相整距绕组感应电机中由于要考虑谐波的作用,转子相数不能简单的按照m相来折算,否则定转子之间的互感参数将难以给定。例如,对于双Y移30°的六相感应电机,对基波可以视为六相系统,但是对三次谐波是一个两相系统[4]。
针对上述问题,本文采用多回路理论[6-7]建立了多相感应电机的机电动力系统模型,其优点是考虑转子的实际槽数和排布,避免传统的建模方法中所必需的简化和折算。从绕组的空间排布出发推导出各互感参数与空间位置角的线性关系,既简化了参数的计算,又考虑了各次谐波的影响,因此具有较好的通用性和准确性。
1 基于多回路理论的分析模型
如果将感应电机视为一系列由单个线圈(或单个回路)构成的电路结构,可以采用多回路理论建立感应电机的分析模型。采用这一分析模型时,对感应电机作如下的基本假设:①假设定子内表面、转子外表面光滑,以等效气隙长度反映定、转子开槽对气隙磁导的影响;②不计铁磁材料饱和、磁滞、涡流影响和导电材料趋肤效应的影响。
在上述假设之下,可以列写出通用的电压方程、磁链方程和状态方程,其转矩方程和转子运动方程与一般无异,限于篇幅,不再赘叙。
1.1 定子电压方程
假设定子相数为m,可以列写定子电压方程

式中:Us=[us1us2… usm]T是定子电压;Is=[is1is2… ism]T是定子电流;ψs=[ψs1ψs2… ψsm]T是定子磁链;Rs=rsEm×m是定子阻抗矩阵;Em×m是 m ×m维的单元矩阵。
1.2 转子电压方程
对于导条数为n的鼠笼转子,可以视为n个回路。设每个回路中的导条电阻为rb,端环电阻为re,那么根据图1,对第i个回路可以列写回路方程[7]
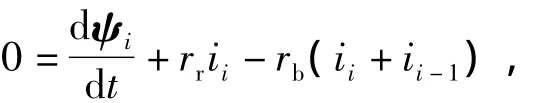
其中rr=2(rb+re)为回路总的电阻;因此对于整个转子回路可以列写回路方程

式中:Ir=[ir1ir2… irn]T为转子电流;ψr=[ψr1ψr2… ψrn]T为转子回路磁链;

为转子电阻矩阵。

图1 转子导条回路Fig.1 Current-loops in rotor
将式(1)和式(2)的定子电压方程和转子电压方程写在一起,可得

1.3 磁链方程
定转子的磁链方程为
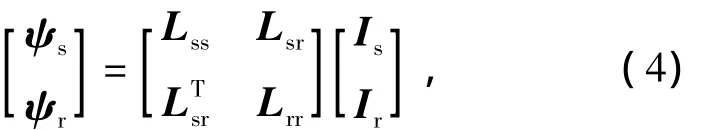
式中:Lss为定子绕组的互感矩阵;Lsr为定转子回路之间的互感矩阵;Lrr为转子导条回路之间的互感矩阵。
1.4 状态方程
根据电压方程和磁链方程,可以推导出电流的状态方程。将式(4)代入式(3)中可得式中:θr为对基波而言转子旋转的电角度;ωr为转子旋转的电角速度。

2 参数模型的参数计算方法
式(1)~(5)给出了基于多回路理论的m相感应电机的分析模型,其中式(5)中的电阻矩阵可以通过实测或者计算值给定,需要计算的主要是各互感参数及其对电角度的导数。值得说明的是,文献[7-8]中均以级数分解的形式给出了互感参数的表达式,这种表达方法比较繁琐,而且只能考虑到有限次谐波。下面通过推导各互感参数与电角度差的关系,给出互感参数的线性表达式,不仅形式简洁,利于编程实现,而且可以穷尽所有谐波,不存在截断误差。
2.1 定子绕组之间的互感矩阵Lss
假设定子绕组每相串联的匝数为Ns,通入的电流为I1,极对数为p,对于整距绕组,在一个电角度内气隙磁势的分布如图2(a)所示。假设两套定子绕组之间的电角度差为 Δθs,当 Δθs=0时,表示任一相绕组主电感;当Δθs=π时,表示两套绕组刚好相位相反,其互感等于主电感的负值;当Δθs=2π时,与 Δθs=0 相当;当 Δθs在[0,2π)的范围内变化时,由于每一相产生的是矩形波磁势,因此两相绕组之间的互感随Δθs线性变化,其互感关系如图2(b)实线所示。考虑定子相绕组的漏感,定子绕组第i相与第j相之间的互感为
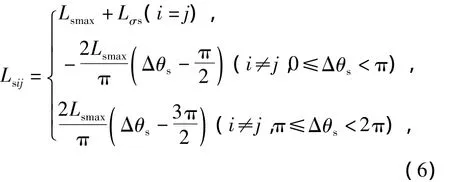
式中:Lσs是定子绕组的漏感;Lsmax为定子绕组的主电感,且
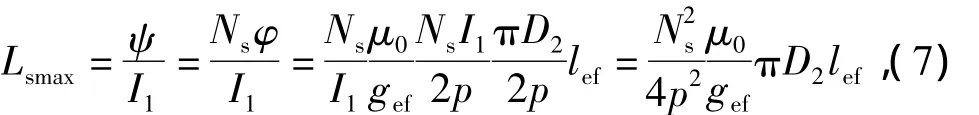
式中:μ0是真空磁导率;gef是气隙的有效长度;D2是定子内径;lef是铁心有效长度。
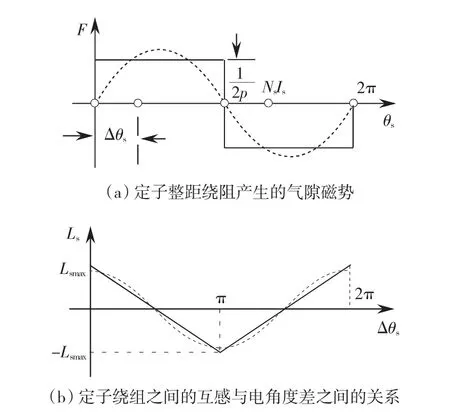
图2 定子绕组之间的互感与电角度差之间的关系Fig.2 Relationship between the mutual-inductance of stators and the difference of electrical angle
从上述的推导可知,定子绕组产生的磁势是矩形波,含有各种奇数次谐波,而在互感的推导中,磁链ψ是矩形波磁势产生的磁链;因此这种方法推导的互感包含了各种谐波的影响,而且具有简洁的表达形式。如果只考虑基波,那么定子每相绕组产生的磁势如图2(a)虚线所示,两相绕组之间的互感关系如图2(b)虚线所示,从图2(b)可见,两种方法的计算结果存在较大区别,当然,对于分布整距绕组,每极每相槽数越大,这种区别就越小。由此可见,这种参数的计算方法较好地考虑了各次谐波的影响,而且比较简洁,在下文的参数推导中均采用了这一方法。
2.2 转子导条回路之间的互感矩阵Lrr
假设转子导条数为n,某一导条回路产生的气隙磁势分布如图3(a)所示(n=6),其中以圆圈表示导条截面。设两个导条之间的电角度为Δθr,图3(b)给出了两个导条回路之间的互感与电角度Δθr之间的关系,由于Δθr是离散的,因此对应的任意两个导条之间的互感也是离散的,以黑圈表示。考虑转子导条回路之间的漏感,可以得到第i个转子导条回路与第j个转子导条回路之间的互感

式中:Le是端部产生的漏感;Lb是导条产生的漏感。采用式(15)的推导方法,Lrmax和 Lrmin分别给定为


图3 转子导条回路之间的互感与电角度差之间的关系Fig.3 Mutual-inductance of rotor relative to difference of electrical angle
2.3 定转子之间的互感
假设定子某一相绕组产生的气隙磁势分布如图4(a)所示,转子某一导条回路与该相定子绕组之间的电角度差为 Δθsr。当 Δθsr在[0,2π)内变化时,定转子之间的互感参数变化如图4(b)所示。根据上述的关系,考虑各次谐波之后的定转子之间的互感为

式中:Δθsr(0)是初始的角速度;ωr是转子旋转的电角速度。Lsrmax的计算式为


图4 定转子互感与电角度差之间的关系Fig.4 Mutual-inductance of stator winding and rotor loop relative to difference of electrical angle
2.4 定转子互感矩阵对电角度的导数
根据图4(b)所示的定转子之间互感关系,可以给出相应的互感参数对电角度的导数关系如图5所示,其表达式为


图5 定转子互感大小对电角度的求导Fig.5 Derivative of mutual-inductance of stator winding and rotor loop with respect to difference of electrical angle
2.5 饱和对参数的影响
实际电机中或多或少的存在一定程度的饱和,由于饱和的存在,使得齿部和轭部存在一定程度的磁压降。假设一相绕组产生的总的磁势为Fm,则

式中:Fδ是气隙磁势;Ft1,Ft2分别为定转子齿部磁压降;Fj1,Fj2分别为定转子轭部磁压降。定义饱和系数

根据式(14)的计算方法,互感参数满足

其中K是比例系数,与匝数、极距和铁心有效长度有关。考虑饱和以后,互感参数满足

即考虑饱和后,需要将式(14)的互感参数除以Ks(或者将等效的气隙长度增加为Ksgef)。值得说明的是,这一处理方法并不能反映饱和时气隙磁场畸变产生的高次谐波。
3 样机算例及其分析
根据上述的机电动力系统模型,对一台15相、45 kW、4极的样机在非正弦供电(注入三次谐波)下的空载起动与负载运行进行了仿真分析,并与试验结果进行了对比。外加电压基波分量频率为f1=20 Hz,有效值为U1=140 V,注入的三次谐波频率为f2=60 Hz,有效值为 U2=23.3 V(U2=U1/6),空载转矩约为15 N·m(按照额定转矩的2%估算)。仿真时,负载转矩初始值设定为Tl=15 N·m,模拟空载的情况,在t=2 s时增加至Tl=262 N·m(输出功率约15.4 kW),待稳定运行后,在t=3.5 s时,负载增加至Tl=388 N·m(输出功率约23.2 kW)。外加电压和负载转矩的波形如图6所示,其中(a)是定子第1相的电压波形us1;(b)是外加负载转矩Tl。图7给出了在此输入条件下的样机起动与负载运行响应图,其中(a)是定子第1相电流;(b)是转子导条电流;(c)是电磁转矩;(d)是转速。从图中可以看出电机起动电流约为额定电流的9倍,电机经过约1.5 s起动完毕,稳定后转速约为600 r/min,增加负载以后,转速略有下降,约为594 r/min左右。为了进一步验证仿真结果的正确性,记录了稳定以后的定子电流并与仿真的定子电流进行了对比。
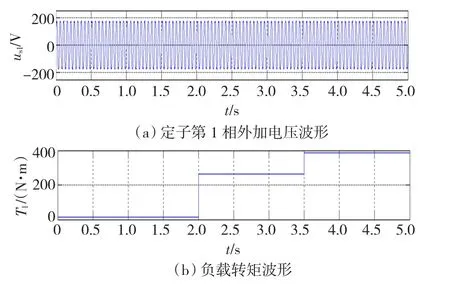
图6 定子第1相外加电压和负载转矩的波形Fig.6 Curves of voltage and load torque applied on phase 1

图7 样机在给定电压和负载下的动态响应仿真曲线Fig.7 Simulation of dynamic performance of prototype machine under given voltage and load torque
图8、图9、图10分别给出了空载、15.4 kW、23.2 kW负载功率时实测电流与仿真电流的对比,各图中图(a)是实测电流,图(b)是仿真电流。表1给出了各种负载情况下的主要谐波分析结果。从图8~图10和表1可以看出,仿真值与实测值很接近,
图8 空载时的实测电流与仿真电流
Fig.8 Measured current and simulative current on no-load说明了这一模型的正确性。当然,仿真结果与实测结果存在一定误差,这可能主要有以下几个方面的原因:①这一模型是基于一定的理想假设条件,没有考虑定转子开槽产生的磁导谐波,没有考虑趋肤效应、温升等造成的参数非线性化;②实际电机的电磁参数难以准确给定;③无法考虑饱和时气隙磁场畸变产生的高次谐波。
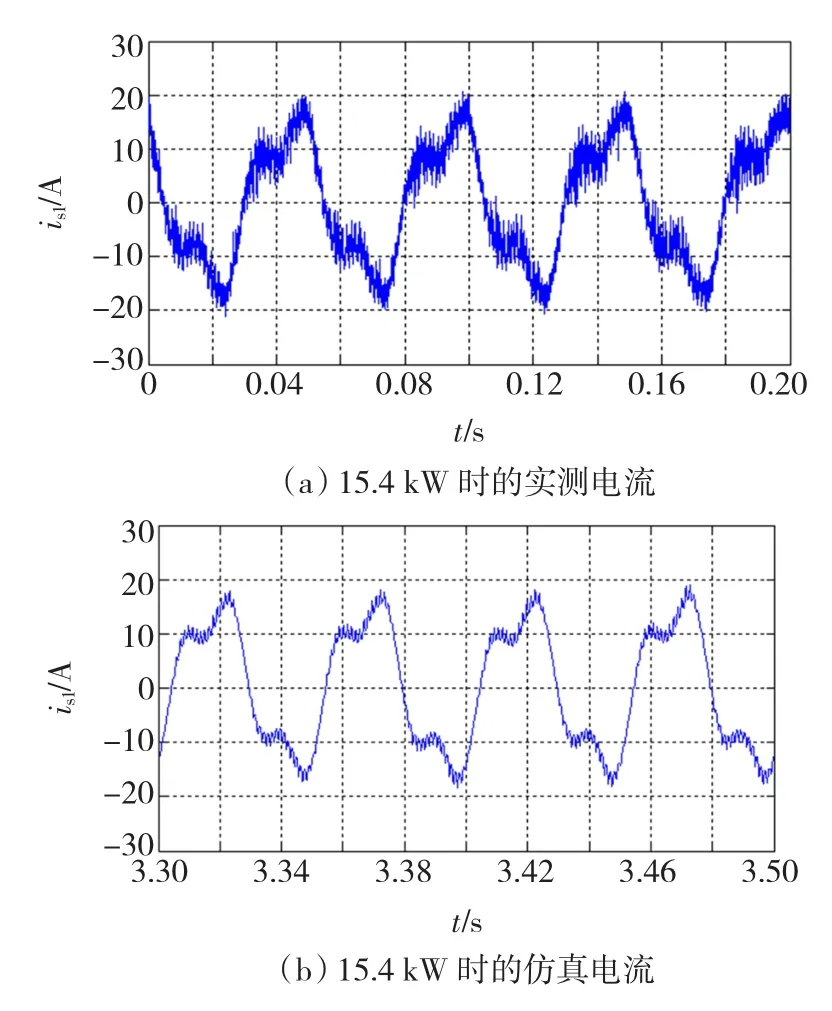
图9 15.4 kW时的实测电流与仿真电流Fig.9 Measured current and simulative current at bearing power of 15.4 kW
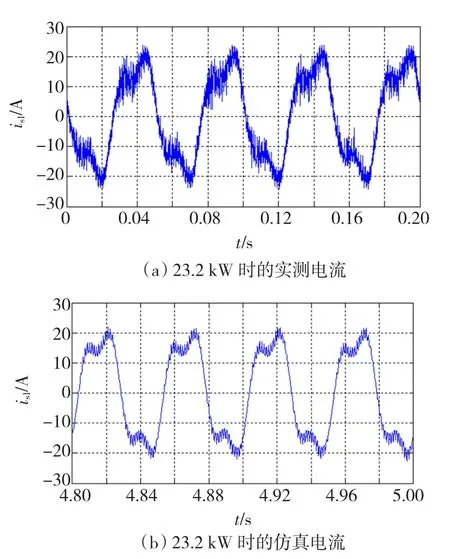
图10 23.2 kW时的实测电流与仿真电流Fig.10 Measured current and simulative current at bearing power of 23.2 kW

表1 不同负载下试验波形与仿真波形的谐波分析结果Table 1 Harmonic analysis results of measured and simulative currents under different loads
4 结论
采用多回路理论建立了多相感应电机的机电动力系统模型,这种基于多回路理论的多相整距绕组感应电机的机电动力系统模型能够客观地反映转子导条的数量和分布,并且具有简洁的参数计算方法,具有良好的通用性与准确性,适用于多相电机在非正弦供电方式下的仿真分析研究。试验与仿真结果的对比验证了这一建模方法的正确性。
当然,由于这一模型是基于一定的理想假设条件,以及实际电机的参数难以准确给定,仿真结果与实测结果存在一定误差。
[1]侯立军,苏彦民,陈林,等.多相感应电机调速系统的发展现状和应用前景[J].微电机,2001,34(5):42-44.
HOU Lijun,SU Yanmin,CHEN Lin,et al.The development state and application prospect of multiphase induction motor drive system[J].Micromotors,2001,34(5):42-44.
[2]TOLIYAT H A,LIPO T A,WHITE J C.Analysis of a concentrated winding induction machine for adjustable speed drive applications(Ⅰ):Motor analysis[J].IEEE Transactions Energy Conversion,1991,6(4):679-683.
[3]TOLIYAT H A,LIPO T A,WHITE J C.Analysis of a concentrated winding induction machine for adjustable speed drive applications(Ⅱ):Motor design and performance[J].IEEE Transactions Energy Conversion,1991,6(4):684-692.
[4]LYRA R O C,LIPO T A.Torque density improvement in a six-phase induction motor with third harmonic current injection[J].IEEE Transactions on Industry Application,2002,38(2):1351-1360.
[5] 辜承林.机电动力系统分析[M].武汉:华中科技大学出版社,2006:144-188.
[6]高景德,王祥珩,李发海,等.交流电机及其系统的分析[M].北京:清华大学出版社,2005:423-427.
[7]刘徽.计及谐波影响异步电机暂态通用仿真算法的研究[J].大电机技术,2000,(5):35-39.
LIU Hui.Generalized modeling and simulation of induction motors taking the harmonic field effect into account[J].Large Electric Machine and Hydraulic Turbine,2000(5):35 -39.
(编辑:张静)
