基于免疫克隆选择算法的无刷直流电动机速度自抗扰控制器优化设计

任海鹏， 朱峰

（西安理工大学信息与控制工程系，陕西西安 710048）

0 引言

永磁无刷直流电动机以其体积小、结构简单、可靠性高、输出转矩大、动态性能好等特点得到了越来越广泛的应用［1］，尤其是在机器人、航天航空、精密电子仪器与设备等对电机性能、控制精度要求较高的场合和领域，无刷直流电机的应用和研究受到了广泛的重视［2］。人们已经尝试将最优控制［3］、基于观测器的控制方法［4］、滑模变结构控制［5］、模糊控制［6］、神经网络控制［7］等方法应用于无刷直流电动机控制系统，但各种方法都有自己的局限性，如何改进这些方法，克服自身的局限性，获得更好的性能是值得研究的问题。

自抗扰控制器是在改进经典PID控制器固有缺陷基础上形成的一种新型控制器［8］，该控制器不仅算法简单，而且可以对系统的内外扰动进行估计并给予补偿，当被控对象参数发生变化或存在不确定性扰动时，仍能得到很好的控制效果，具有较强的鲁棒性［9－10］。但是，由于自抗扰控制器的参数较多，在参数调节时没有成熟的理论依据，只能依据设计者的经验反复调整，得到的参数往往达不到期望的控制效果，更不能实现自抗扰控制器参数的最优整定，无法充分发挥自抗扰控制器的理论效能。

免疫克隆选择是由一种重要的生物免疫学说，根据生物免疫克隆选择原理发展而来的免疫克隆选择算法是一种新的高性能优化方法［11］。一般遗传算法中，交叉是主要算子，变异是背景算子，而克隆选择算法刚好相反，它采用大量无性繁殖和高频变异，并且记忆优势抗体，以便快速识别抗原，提高问题的求解速度。实验表明克隆选择算法的性能强于遗传算法［12］，克隆算子本身具有记忆功能，因此算法本身就能够保证以概率1（最大可能性）收敛到最优解，而简单遗传算法则不能。本文提出用克隆选择算法来优化自抗扰控制器参数，得到了准则函数意义下，（准）最优的自抗扰控制器参数。在免疫克隆算法中抗体亲和度评价是一个重要步骤，考虑到在CCS（Code composer studio）中编制优化程序进行控制器参数在线优化存在如下困难:①数字信号处理器的资源有限，难以实现复杂的免疫克隆选择算法;②某些抗体对应的控制参数，可能导致电机驱动系统的不稳定，甚至是损坏装置和元件;因此，本文调用SIMULINK仿真模型［13］进行免疫克隆选择优化过程中的亲和度计算，这样可以使优化算法自动进行下去，从而避免了复杂的亲和度实验评价过程。电机驱动系统中电流环采样时间短，而自抗扰控制算法计算相对复杂，实现起来实时性较差;而电流环采用自抗扰控制器时，由于微分跟踪器的特性使得电流环调节时间加长，不利于转矩的快速建立，可能导致转矩脉动增大;因此，在本文中自抗扰控制器仅用于转速环的控制，电流环采用PI控制算法，构成双闭环速度控制系统。

1 基于自抗扰控制器的无刷直流电动机控制系统的设计

1.1 系统的硬件结构

无刷直流电动机系统的结构框图如图1所示。系统硬件主要包括由无刷直流电动机、智能功率模块IPM组成的主电路、转子位置、电流、速度的检测电路。软件部分基于TI公司TMS320LF2407A DSP来实现。速度通过光电码盘和DSP的QEP接口检测，电流信号通过霍尔元件和相应的变换电路送入DSP（数字信号处理器Digital signal processor）的A/D转换器实现两相电流检测，位置信号通过通用I/O接口检测，在DSP中利用软件算法实现速度和电流双闭环调节。

图1 无刷直流电动机转速控制系统结构框图Fig．1 Framework of brushless DC motor（BLDCM）control system

1.2 无刷直流电动机的数学模型和电流环控制器的设计

无刷直流电动机的相电压方程为

式中:ux是相电压;R是相电阻;ix和ex（x=a，b，c）分别对应a，b，c三相的相电流和反电动势;L1=L－M，其中L为绕组电感，M为绕组之间互感。

电流子系统方程为

转速子系统方程为

针对电流的动态方程，采用文献［14］的方法设计PI控制器，可以把电流环整定成典型I型系统，完成电流环设计。

1.3 基于自抗扰控制器的速度环设计

自抗扰控制器的结构框图如图2所示，自抗扰控制器由跟踪微分器（TD），扩张状态观测器（ESO）和非线性状态误差反馈控制律（NLSEF）3部分组成。框图中z11是预定的过渡过程;z12是z11微分，z21和z22是状态估计量;z23是扩张状态观测器对系统的补偿量;u为控制量;y为系统实际输出;w是所有扰动的综合。

图2 速度自抗扰控制器结构图Fig．2 Framework of speed active-disturbance rejection controller（ADRC）

自抗扰控制器只需利用系统的时间尺度信息进行控制器设计，不用考虑系统的线性或非线性，时变或时不变。在式（3）中，若令

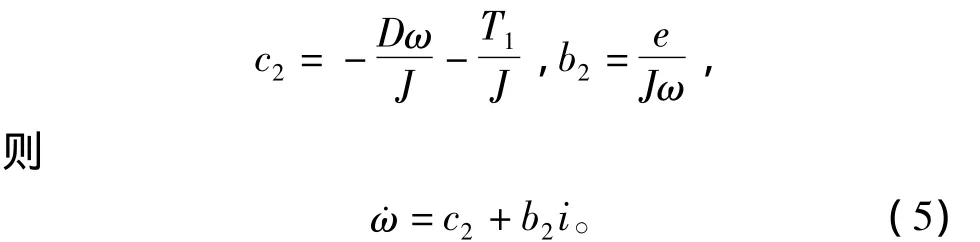
由式（5）可见，无刷直流电动机转速环节也可以近似为一阶积分线性对象，负载和其他扰动可以反映在c2中，对速度动态系统设计自抗扰控制器，其3个部分的动态方程如下。

微分跟踪器（TD）的表达式为

微分跟踪器用来安排过渡过程，快速无超调地跟踪输入信号，具有较好的微分特性，从而避免了设定值突变时，控制量的剧烈变化以及输出量的超调，很大程度上解决了系统响应快速性和超调之间的矛盾。在无刷直流电动机中，电流控制器要控制三相电流频繁在0、正、负负载电流之间变换给定，因此主要要求电流的快速性，这也是在电流环不采用自抗扰控制的一个重要原因。

扩张观测器（ESO）的表达为

式中:ε为给定误差;z21，z22为扩张状态观测器对系统状态的估计量;u 为控制量;α1，β1，β2，δ1，b0为可调参数。

扩张状态观测器是自抗扰控制器的核心部分，它将系统各种不确定因素都归结为对系统的扰动，通过扩张状态观测器估计出系统的状态，同时估计出扰动并给予相应补偿。

非线性反馈控制器（NLSEF）的表达为

式中:ε1为状态误差;β3，α2，δ2为可调参数。

跟踪微分器输出与扩张状态观测器的估计值相比较得到系统状态误差，送入非线性状态误差反馈控制器运算得到控制量，再与扩张状态观测器给出的补偿量求和，得到被控对象的最终控制量。

自抗扰控制器设计过程中，需要调整r，α1，a2，β1，β2，β3，δ1，δ2，以得到期望的控制性能;但是参数整定缺少理论指导，且参数之间的相关性很大，根据经验调整自抗扰控制器参数是繁琐耗时的工作，得到参数的效果也无法达到最优;因此下一节将采用免疫克隆选择算法优化自抗扰控制器参数。

2 基于免疫克隆选择算法的自抗扰控制器参数优化

2.1 免疫克隆选择基本原理

克隆选择原理最先由Jerne提出，Jerne认为:当淋巴细胞实现对抗原的识别（即抗体－抗原的亲和度超过一定阈值）后，B细胞被激活并增殖复制产生大量B细胞克隆，随后克隆细胞经历高频变异过程，产生对抗原具有特异性的抗体。克隆选择理论描述了获得性免疫的基本特性，只有成功识别抗原的免疫细胞才得以增殖。克隆选择的主要特征是免疫细胞在抗原刺激下产生克隆增殖，随后通过变异分化为多样性效应细胞（如抗体细胞）和记忆细胞。克隆选择对应着一个亲合度成熟（Affinity maturation）的过程，即对抗原亲合度较低的个体在克隆选择机制的作用下，经历增殖复制和变异操作后，其亲合度逐步提高而“成熟”的过程;因此亲合度成熟本质上是一个达尔文式的选择和变异的过程，克隆选择原理通过采用变异等算子和相应的群体控制机制实现。

2.2 免疫克隆选择算法的实现

免疫克隆选择算法主要考虑的免疫功能:保持功能性的记忆细胞从指令系统中分离，受刺激最强的个体被选择和克隆，未受刺激的细胞死亡;亲和力成熟和较高亲和力个体克隆的重新选择（re-selection）;多样化个体的产生和保持，与细胞个数成比例的高频变异。其算法具体步骤如下:

①生成侯选解集P，P是由记忆单元（M）和保留种群（Pr）组成，即P=Pr+M;

②根据亲合度测量，选择n个亲和度最强的个体（Pn）;

③复制（克隆）种群中这n个最好的个体，生成一个克隆临时种群（C），克隆规模与抗体－抗原的亲合度成正比;

④对克隆临时种群进行高频变异，获得了变异后的抗体群（C*）;

⑤从C*中重新选择改进的个体组成记忆单元M，P中的一些个体也被C*中其他改进的个体所取代;

⑥利用随机产生的新抗体代替P中d个旧抗体（引入多样性），亲合度低的抗体更容易被取代。

克隆选择算法流程如图3所示。该算法与一般遗传算法相比的不同点在于:首先，将基于概率的轮赌选择变为基于抗体－抗原亲合度（适应度）的比例选择;其次，构造了记忆单元，从而将遗传算法记忆单个最优个体变为记忆一个最优解的群体;另外，通过随机新抗体的引入，增加了种群多样性。

2.3 亲和度函数的定义及其计算方法

本文中亲和度定义为

式中:e（k）为e（t）=z（t）－y（t）的采样值，z（t）为系统给定，y（t）为在特定自抗扰控制器参数情况下BLDCM的输出转速;Kg为恒值常数，用来增加误差敏感度;η为很小的正常数，用来避免计算过程异常情况下出现的除零问题。

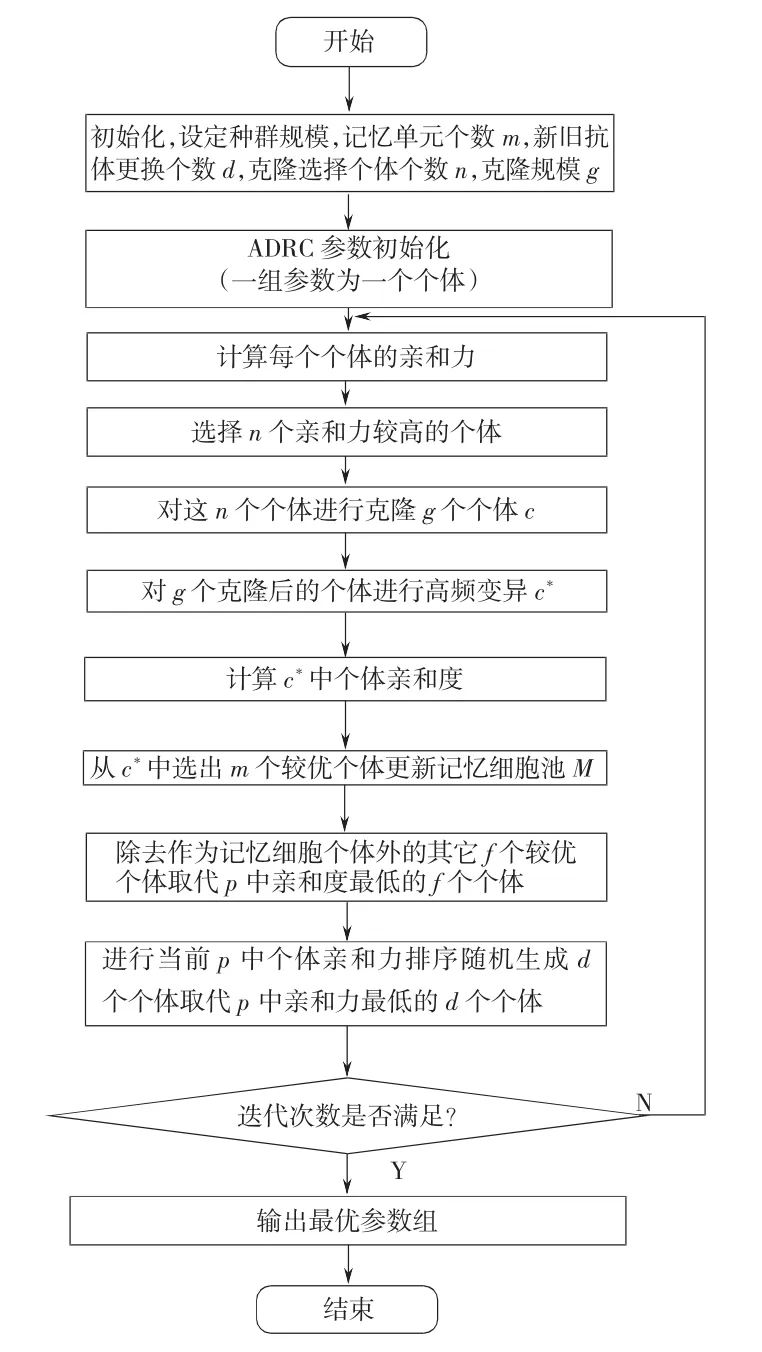
图3 参数优化流程图Fig．3 Flow chart of parameter optimization

亲和度计算的过程需要得到无刷直流电动机在特定控制器参数下的输出y，如果通过实验来得到y，显然是很困难的。为此，在MATLAB中建立了无刷直流电动机的器件模型，并构建了基于自抗扰控制器的控制系统仿真模型，利用该模型可以得到特定参数下的y（t）。采用SIMULINK建立模型的另一个好处是可以在M文件中调用该模型经行仿真得到y（t），并基于M文件中的程序自动运行克隆选择算法中除亲和度计算外的其他部分，得到最终优化结果。这一点是其他电力电子电路仿真软件如EWB，ORCAD 等所不具备的［13］。

本文建立的整个电机控制系统仿真模型如图4所示。图4中BLDCM为无刷直流电动机的器件模型，该模型中各功能模块中尽可能使用SimPower-System的工具箱的器件模型封装构建，例如图5和图6分别为相电压电流转换模块和逆变器模型。仿真模型中所用电机的参数为电机标称参数，额定转矩为0.75 N·m，额定转速为2 000 r/min，相电感为12.6 mH，极对数为3，额定线电压为97 V，系统转动惯量为0.66 kg·m2，电枢绕组电阻为12 Ω，反电势系数为 0.047 5 V/（r·min－1）。

图4 无刷直流电动机速度控制系统的仿真模型Fig．4 Simulation model of BLDCM speed control system

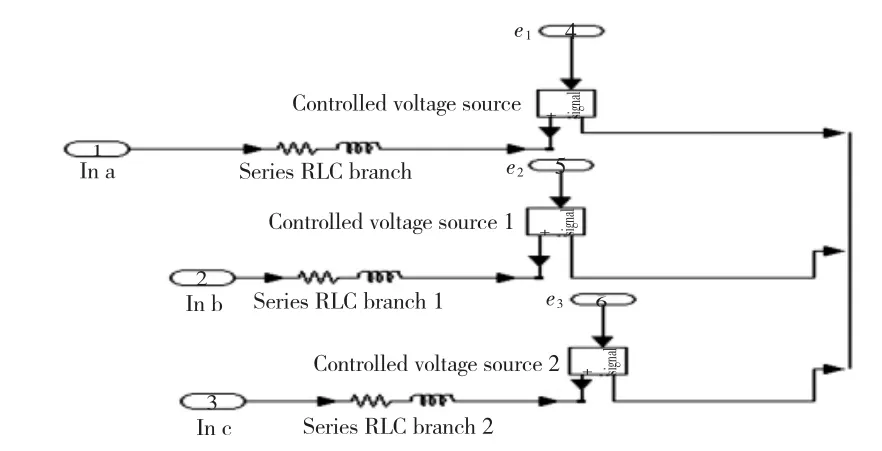
图5 电压电流转换模块Fig．5 Conversion module of voltage and current

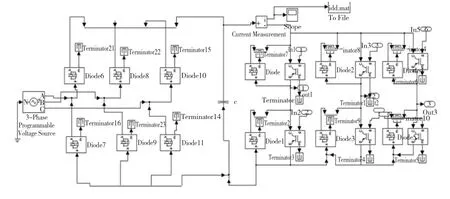
图6 逆变器模型Fig．6 Simulation model of inverter

3 试验结果

仿真中免疫算法参数如下配置:二进制编码，编码长度为22位，种群规模p=30，记忆单元个数m=10，待克隆个体规模n=10，克隆临时种群规模g=40，被取代适应度低的旧个体数 f=5，重新初始化个体数d=3。

试验系统是由无刷直流电动机，驱动系统和负载构成，负载为一直流发电机。采用传统的电流环设计方法［14］，设计电流环参数，根据经验反复调整设计自抗扰控制参数进行电机控制，得到试验结果如图7所示。

本文试验中突加负载用给发电机突加励磁的方式实现，突加负载后负载变化约为额定负载的50%。示波器图中的速度图是利用光电码盘检测速度，通过单片机计算速度，再将速度通过D/A转换变成电压值。采用本文克隆选择算法只优化外环的自抗扰控制器，得到的自抗扰控制器参数对无刷直流电动机进行控制，得到试验结果如图8所示。对比图7和图8可见，优化后控制器，在响应速度稍快的前提下，在突加负载时的转速降落明显减小，转速恢复时间短，抗扰能力有了很大提高。另外在相同电流环参数的情况下，图7中未优化控制器的转矩脉动较大，速度稳态波动也较优化后控制器大。

图7 采用经验设计ADRC参数得到的实验结果Fig．7 Experimental results with experienced ADRC parameters

图8 优化ADRC参数后的实验结果Fig．8 Experimental results with optimized ADRC parameters

为了进一步改善系统性能，对速度环的自抗扰控制器和电流环PI的参数同时进行优化。采用优化后参数控制无刷直流电动机，首先对抗扰能力进行了实验，结果如图9所示。为了比较电流环优化效果，对优化前后电流波形进行了比较，结果如图10所示。可见在双环优化后速度抗扰性能基本不变的前提下，电流波形有较明显改善。

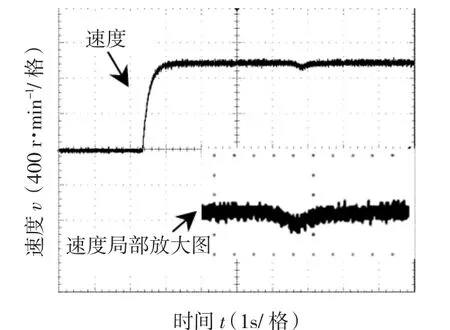
图9 优化ADRC和PI参数后的速度响应Fig．9 Speed response with optimized PI and ADRC parameters

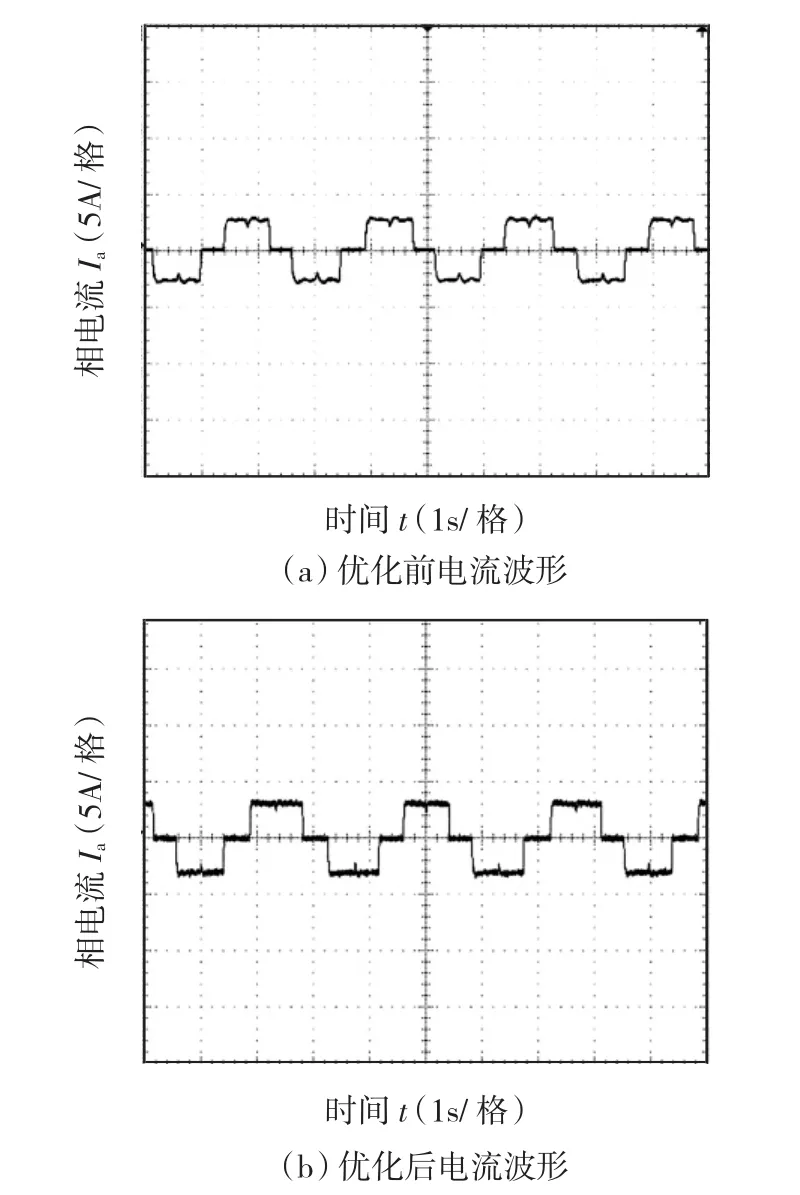
图10 优化ADRC和PI参数前后的电流波形Fig．10 Current curves before and after optimization

4 结论

利用免疫克隆选择算法实现了自抗扰控制器的参数优化，为了解决亲和度函数评价问题，利用MATLAB的SIMULINK建立了标称参数下无刷直流电动机的器件模型，在M文件中编制免疫克隆选择算法，调用SIMULINK模型进行亲和度评价，实现了免疫克隆选择算法优化自抗扰控制器参数。试验结果表明，经过优化后的自抗扰控制比优化前的自抗扰控制调节时间减小，抗干扰能力增强，转矩特性更好。

［1］张琛．直流无刷电动机原理及应用［M］．北京:机械工业出版社，2004:8－11．

［2］PILLAY P，KRISHNAN R．Modeling，simulation，and analysis of permanent-magnet motor drives（PartⅠ）:the permanent-magnet synchronous motor drive ［J］．IEEE Trans．on Industry Applications，1989，25（2）:265 －273．

［3］许镇琳，吴忠，王秀芝，等．无刷直流伺服电机换向最优控制［J］．自动化学报，1996，22（4）:428－435．

XU Zhenlin，WU Zong，WANG Xiuzhi，et al．Optimal communication control of brushless DC motor［J］．Acta Automatica Sinica，1996，22（4）:428－435．

［4］龚金国，任海鹏，刘丁．带负载转矩补偿的无刷直流电动机速度控制［J］．电机与控制学报，2005，9（6）:550－553．

GONG Jinguo，REN Haipeng，LIU Ding．Speed control of brushless DC motor drivers by load torque estimation［J］．Electric Machines and Control，2005，9（6）:550 －553．

［5］LEE C K，KWOK N M．A BLDCM servo system using a variable structure controller with an adaptive switching slope［C］∥Proceeding of IEEE Power Electronics Specialists Conference．Atlanta:IEEE Press，1995，2:1352 －1357．

［6］任海鹏，杨延西，刘丁．基于无刷直流电动机直接驱动的机床位置伺服系统的智能双模控制的研究［J］．机床与液压，1999（6）:18－20．

REN Haipeng，YANG Yanxi，LIU Ding．On intelligent bi-mode control of brushless DC motor directly drive machine tool［J］．Machine Tool and Hydraulic，1999（6）:18－20

［7］EI-Sharkawi M A，EI-Samahy A A，EI-Sayed M L．High performance drive of DC brushless motors using neural network［J］．IEEE Trans．on Energy Conversion，1994，9（2）:317 －322．

［8］韩京清．自抗扰控制器及应用［J］．控制与决策，1998，13（1）:19－23．HAN Jinqing．Auto-disturbances-rejection controller and its applications［J］．Control and Decision，1998，13（1）:19 －23．

［9］夏长亮，李正军，杨荣，等．基于自抗扰控制器的无刷直流电动机控制系统［J］．中国电机工程学报，2005，24（2）:82－86．

XIA Changliang，LI Zhengjun，YANG Rong，et al．Control system of brushless DC motor based on active-disturbance rejection controller［J］．Proceeding of CSEE，2005，24（2）:82 －86．

［10］任海鹏，张继祖，李琦，等．基于自抗扰控制器的无刷直流电动机速度控制［J］．电气传动，2008，38（4）:46－50．

REN Haipeng，ZHANG Jizu，LI Qi，et al．Brushless DC motor speed control based on active disturbance rejection controller［J］．Electric Drive，2008，38（4）:46 －50．

［11］CASTRO L N，VON ZUBEN F J．Learning and optimization using the clonal selection principle［J］．IEEE Trans．on Evolutionary Computation，2002，6（3）:239－251．

［12］焦李成，杜海峰，刘芳，等．免疫优化、计算、学习与识别［M］．北京:科学出版社，2005:12．

［13］任海鹏，刘丁．基于MATLAB的PFC boost变换器仿真研究和实验验证［J］．电工技术学报，2006，21（5）:29－35．

REN Haipeng，LIU Ding．Simulation on power factor correction boost converter based on matlab and its experimental verification［J］．Transactions of China Electrotechnical Society，2006，21（5）:29－35．

［14］任海鹏，刘丁，李琦．DSP在无刷直流电动机伺服系统中的应用［J］．微电机，2000，33（2）:21－24．

REN Haipeng，LIU Ding，LI Qi，Application of TMS320F240 DSP in brushless DC motor servo system［J］．Micromotors，2000，33（2）:21－24．

（编辑:张静）