直接驱动XY平台轮廓误差分析及法向交叉耦合控制
2010-02-10王丽梅武志涛孙宜标金抚颖
王丽梅, 武志涛, 孙宜标, 金抚颖
(沈阳工业大学电气工程学院,辽宁沈阳 110178)
0 引言
随着复杂型面零件加工精度要求的不断提高,机床进给系统的轮廓加工精度已成为其重要的精度指标。XY平台系统的轮廓误差是由轮廓运动所涉及的X、Y两轴的位置误差共同决定。在直线电机直接驱动XY平台的机械加工中,负载扰动、进给系统的机械延迟以及两轴驱动系统参数不匹配等因素对XY平台的轮廓加工精度产生较大影响[1]。
为提高XY平台系统的轮廓精度,许多研究方法侧重于设计控制器以减小单轴的跟踪误差,进而减小整个系统的轮廓误差[2]。Koren首先提出了交叉耦合(Cross-coupled)控制以减小轮廓误差的思想[3]。文献[4-5]设计了交叉耦合轮廓控制器以提高多轴CNC机床的轮廓精度。已有的研究表明,传统交叉耦合控制系统较之常规的非耦合控制系统有更好的轮廓精度,但不足在于对任意曲线轨迹轮廓误差系数的计算量较大,控制器设计复杂。
本文将永磁同步直线电机(PMLSM)作为XY平台的驱动部件以发挥其可直接驱动的优点,采用H∞速度反馈控制、零相位误差跟踪控制(ZPETC)与法向交叉耦合控制相结合的策略对两轴的运动进行协调控制,实现跟踪精度与轮廓精度的同时提高。H∞速度反馈控制具有较强的鲁棒性,可消除扰动对系统的影响。在单轴控制回路中引入ZPETC以削弱系统的机械延迟效应,提高系统的跟踪精度。法向交叉耦合控制器作用于两轴之间,将轮廓误差作为直接被控目标,根据各轴的反馈信息,进行实时补偿控制,可有效提高轮廓精度。
1 XY平台的轮廓误差分析
XY平台由两台PMLSM直接驱动轴向相互垂直的XY两轴进行平面运动,以完成精密轨迹运动。运动中各轴的跟踪误差不协调反映到轨迹曲线轮廓上形成轮廓误差,如图1所示,其中R为指令位置,P为实际加工位置,ε为轮廓误差,e为跟踪误差。
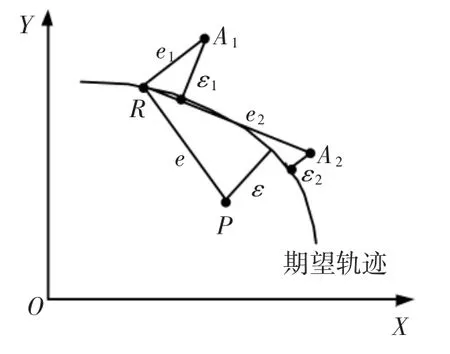
图1 跟踪误差与轮廓误差Fig.1 Tracking error and contour error
对于任意曲线轨迹轮廓,如图2所示,P(Xa,Ya)为实际加工位置,(Xo,Yo)为实际位置的曲率中心,ρ为曲率半径,θ为期望轨迹R点的切线与X轴的夹角,ex为X轴位置误差,ey为Y轴位置误差,ε'为近似轮廓误差。

图2 任意轮廓曲线的轮廓误差Fig.2 Contour error of arbitrary contour trajectory
传统轮廓误差计算为

达到XY平台的高精度要求需要同时满足跟踪精度和轮廓精度。单独提高各轴的跟踪精度并不能很有效地解决两轴共同作用时的轮廓精度问题,图1中,A1与A2比较,A1点的跟踪误差e1小,但其轮廓误差ε1大于ε2,因此需要综合考虑设计轮廓控制器与单轴控制器协调配合,使实际位置尽可能趋近于指令位置,达到高精度要求。
2 XY平台的控制器设计
对于PMLSM采用d-q坐标系下的模型,电流内环采用电流在d轴上的分量id=0的控制策略,使定子电流矢量与永磁体磁场在空间上正交,其机械运动方程为

式中:iq为q轴上的定子电流;B为黏滞摩擦系数;Fe为电磁推力;FL为负载阻力;Kf为推力系数;M为动子及所带负载的总质量;v为速度。令iq为输入量,v为输出,则被控对象模型的传递函数为

2.1 H∞速度反馈控制
为了减小或消除PMLSM存在的负载扰动对系统鲁棒性的影响,设计速度环H∞反馈控制器,使实际被控对象的输出趋近于标称被控对象的输出[6]。设δ1(t),δ2(t)分别为系统中B/M和1/M的不确定摄动参数,依据PMLSM运动方程可写出增广被控对象的状态空间方程为

式中:状态变量x=[X1X2]T,X1为标称被控对象与实际被控对象的速度输出误差,X2为该误差的积分项;ξ为干扰信号;u为控制输入信号;z为评价信号;加权系数q1>0,q2>0用来调整允许误差量。为充分考虑扰动的影响,ξ项的系数取摄动范围内的最大值,则可将问题归结为如下的H∞鲁棒性能准则设计问题。
设具有参数摄动及外部扰动的被控对象

有正定解 X>0,其中 R2=I+λ-2FTbFb,则状态反馈控制器为

控制输入为u=Kx,K=[K1K2],使得闭环系统满足H∞鲁棒性能准则:对于任意的Q∈Ω,闭环系统内部稳定;ξ到 z的传函 Tzξ(s)满足‖Tzξ(s)‖ <1。
假设摄动最大值已知,即|δ1(t)|≤σ1,|δ2(t)|≤σ2,且 σ1>0,σ2>0 为已知常数,取

则有Q∈Ω且ΔA和ΔB满足式(8)。利用MATLAB求解式(9)、(10)即可求得需要的控制器K。
2.2 零相位误差跟踪控制(ZPETC)
XY平台驱动系统在跟踪控制时,由于存在着电磁惯性和机械惯性使输出响应和输入指令之间存在滞后现象,两信号间存在着较大的相位误差。为补偿时间延时对系统跟踪精度的影响,采用Tomizuka提出的零相位误差跟踪控制(ZPETC),它是一种结合零、极点对消和相位对消,能在较大的带宽范围内对闭环动态系统进行逆处理的前馈控制[7]。实际被控对象的传递函数为式(5)中的G(s),标称对象传递函数为G(s)=,单轴位置控制器参数
n为K,则基于H∞速度反馈控制的闭环系统传递函数为

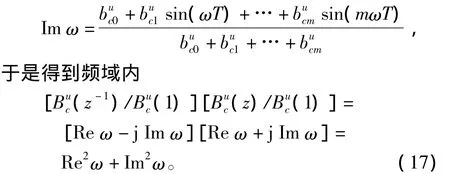
2.3 法向交叉耦合控制
为了解决两轴驱动系统参数不匹配对轮廓精度的影响,在单轴控制的基础上采用交叉耦合控制方法进行实时补偿控制,实现跟踪误差与轮廓误差的同时减小[8],其控制思想是将各轴的误差在耦合控制器中首先进行综合,然后将综合后的误差信息分配给各轴以产生相应的实时附加补偿作用。设Cx和Cy为交叉耦合控制器的耦合增益[4],则

传统轮廓耦合增益需要计算轮廓轨迹的二阶微分,本文采用一种简单近似算法将其化为只需计算一阶微分的法向单位向量。考虑实际位置、指令位置及期望轨迹之间的几何关系,将实际位置与过期望轨迹上指令位置点的切线的垂直距离向量定义为估计轮廓误差向量。在高精度直线伺服系统中,跟踪误差较小,估计轮廓误差向量可以近似为实际轮廓误差向量,如图2所示,可以直接计算轮廓误差向量的幅值ε·为

设跟踪误差向量e和期望轨迹上指令位置处的法向向量n为





基于H∞速度反馈控制和ZPETC的XY平台法向交叉耦合控制框图如图3所示,Xd,Yd和 Xa,Ya分别表示各轴的位置输入输出,ξx和ξy为X、Y轴的扰动项,Kx与Ky为X、Y轴的位置控制器,Ⅰ、Ⅱ表示X、Y轴的零相位跟踪控制器,Ⅲ、Ⅳ表示X、Y轴的H∞速度反馈控制器,Ⅴ表示法向交叉耦合控制器。
以内蒙古自治区阿荣旗为研究区域,以自治区全国第一次地理国情普查数据、森林资源二类调查小班数据、Landsat-OLI遥感影像为研究资料,设置并提取RS与GIS因子作为自变量,以小班的平均平方千米蓄积量作为因变量建立基于最小二乘估计的多元线性回归模型,反演2016年立木蓄积量,对森林蓄积量的遥感估测做了相关研究。
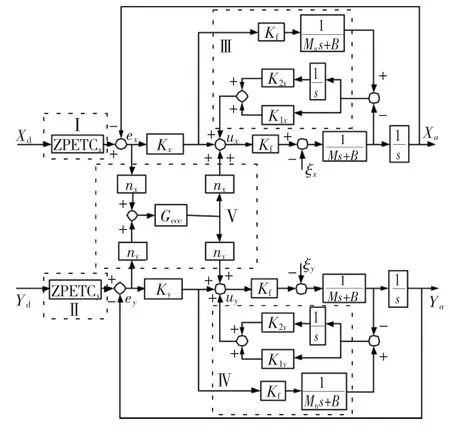
图3 XY平台综合控制框图Fig.3 Block diagram for XY table control system
3 仿真结果及分析
采用2台参数相同的永磁同步直线电机作为XY平台的驱动部件进行仿真研究,电机参数为Mn=11.0 kg,B=8 N·s/m,Kf=29 N/A,动子质量变化为M=1.1 Mn(Mn为动子质量,B表示粘滞摩擦系数,Kf`表示推力系数,M代表变化后的动子质量)。X、Y轴的期望轨迹分别为Xd(t)=10sin(πt)mm,Yd(t)=10sin(π(t+0.5))mm,即轮廓轨迹为不规则椭圆,采样周期为0.001 s。
选取B/M和1/M的不确定摄动参数最大值为σ1=0.25,σ2=0.125,反复试选加权系数得到q1=50,q2=2500,λ=3.1。根据式(9)(10)通过MATLAB 求得H∞控制器为[K1xK1y]=[K2xK2y]=[72 2511]。

为便于比较,对传统PI控制的系统也进行了仿真,权衡稳定性和跟踪性的要求,其比例、积分增益分别为kpx=69,kix=28,kpy=71,kiy=28.7,仿真结果如图4和图5所示。
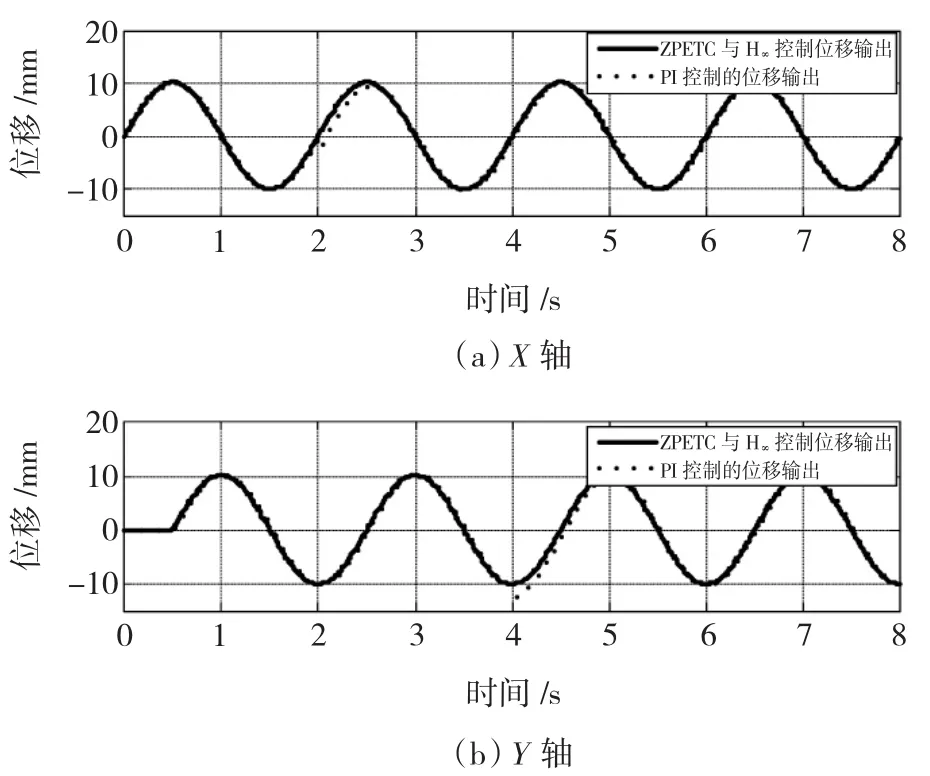
图4 不同控制方法在负载扰动下的X、Y轴位移输出曲线Fig.4 Position responses of X axis and Y axis using different controllers with load

图5 不同控制方法在负载扰动下的单轴跟踪误差输出曲线Fig.5 Tracking errors of X axis and Y axis using different controllers with load
由图4、图5可看出,传统PI控制下的输出响应具有一定的延迟,并且在突加扰动后波动较大,恢复时间较长,而ZPETC与H∞速度反馈控制下的系统位移基本无滞后,跟踪误差较小,具有较强的跟踪性和抗扰性。
由于系统实时性较强,交叉耦合控制器Gccc采用PID控制形式,针对上述两轴参数不匹配情况,经反复调试得其比例、积分、微分增益分别为kp=1 255.4,ki=100 000,kd=42,仿真结果如图6所示。

图6 不同控制器在参数不匹配时的轮廓误差输出曲线Fig.6 Contour errors of XY table using different controllers with parameter mismatch of two axes
由图6可看出,单轴ZPETC与H∞速度反馈控制虽能保证系统的跟踪精度和抗扰性,但其轮廓误差仍然很大,而加入法向交叉耦合控制的系统轮廓精度大幅度提高,能够达到系统高精度要求。
4 结论
采用ZPETC控制、H∞速度反馈控制及法向交叉耦合控制相结合的策略有效地削弱机械系统的时间延迟效应、负载扰动以及两轴驱动系统参数不匹配等因素对直线电机直接驱动XY平台轮廓加工精度的影响。H∞速度反馈控制提高了系统的鲁棒性,ZPETC实现了快速准确跟踪,基于ZPETC与H∞速度反馈控制的法向交叉耦合控制在保证系统跟踪性和鲁棒性的同时大幅度减小了系统轮廓误差。仿真结果表明,所设计控制系统具有较好的跟踪性、鲁棒性和轮廓精度。
[1]王广炎,张润孝,帅梅,等.数控机床的轮廓误差的控制[J].机床与液压,1999,6(1):59-61.
WANG Guangyan,ZHANG Runxiao,SHUAI Mei,et al.Contour error controller in NC machine tools[J].Machine Tool&Hydraulics,1999,6(1):59 -61.
[2]王波,梁迎春,董申.超精密机床模糊轮廓控制技术研究[J].哈尔滨工业大学学报,2005,37(6):830-832.
WANG Bo,LIANG Yingchun,DONG Shen.Fuzzy contour control strategy for the ultra precision machine tool[J].Journal of Harbin Institute of Technology,2005,37(6):830 -832.
[3]曲永印,赵希梅,郭庆鼎.基于零相位误差跟踪控制器的轮廓误差交叉耦合控制[J].中国机械工程,2006,17(11):1135-1137.
QU Yongyin,ZHAO Ximei,GUO Qingding.Cross coupling control of contour errors based on zero phase error tracking controller[J].China Mechanical Engineering,2006,17(11):1135 -1137.
[4]SUN Dong,SHAO Xiaoyin,FENG Gang.A model-free cross-coupled control for position synchronization of multi-axis motions[J].IEEE Transactions on Control Systems Technology,2007,15(2):306-314.
[5]CHENG Mingyang,LEE Chengchien.Motion controller design for contour-following tasks based on real-time contour error estimation[J].IEEE Trans.on Industrial Electronics,2007,54(3):1686-1695.
[6]蓝益鹏,郭庆鼎.直线电动机伺服系统的鲁棒H∞控制[J].电工技术学报,2003,18(5):54-58.
LAN Yipeng,GUO Qingding.Robust H∞control for linear motor servo system[J].Transactions of China Electrotechnical Society,2003,18(5):54-58.
[7]赵希梅,郭庆鼎.为提高轮廓加工精度采用 DOB和ZPETC的直线伺服鲁棒跟踪控制[J].电工技术学报,2006,21(6):111-114.
ZHAO Ximei,GUO Qingding.Linear servo robust tracking control based on DOB and ZPETC to improve the contour machining precision[J].Transactions of China Electrotechnical Society,2006,21(6):111-114.
[8]YEH Syh-Shiuh,HSU Pau-Lo.Estimation of the contouring error vector for the cross-coupled control design[J].IEEE/ASME Trans.on Mechatronics,2002,7(1):44 -51.
(编辑:张静)
