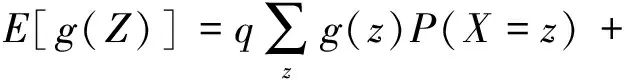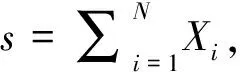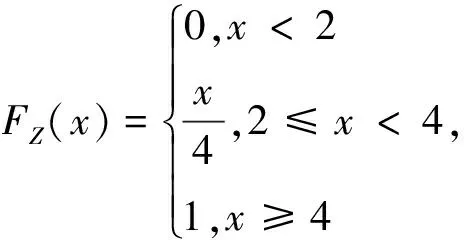混合分布与风险

王丙参,罗英勇,田玉柱

(1.天水师范学院 数学与统计学院,甘肃 天水 741001;2.河南大学 数学与信息科学学院,河南 开封 475001)

在统计学中，所有随机变量(r.v)或者是离散型或者是连续型，然而保险领域却不总这样，许多被用来模拟保险理赔支付的分布函数(cdf)有连续部分，同时也有离散的、正的跳跃部分.例如，在责任险中，理赔额有很大的取值范围，每一种理赔额都对应一个非常小的发生概率.有两种例外情况不容忽视：无理赔(理赔额为0)发生的概率很大，以及理赔额等于最大保险金额的概率(即损失超过某一门限值的概率)，能够产生这种类型r.v的一个简单而灵活的模型是混合模型[1].本文研究了混合分布的性质，引出用微分法构造混合风险的形式，作为保险风险中最常见的应用，给出保费的确定方法.

1 预备知识

微分dF(x)=FX(x)-FX(x-dx)表示x点概率，即若有概率存在，则该微分表示cdf在x点的跳跃高度.若在x处cdf没有跳跃，则该微分等于F′(x)dx，其中dx表示一个无穷小量.在寿险中，R-S积分也称为广义黎曼积分.

定理1[2]条件期望具有下面的性质:

(1)E(aξ+bη|G)=aE(ξ|G)+bE(η|G)，其中a,b∈R，且假定E(aξ+bη|G)存在；

(2)E[E(ξ|G)]=E(ξ)；

(3)如果ξ为G可测，则E(ξ|G)=ξ；

(4)如果ξ与σ代数G独立，则E(ξ|G)]=E(ξ)；

(5)如果G1是σ代数G的子σ代数，则E[(E(ξ|G))|G1]=E(ξ|G1)；

(6)(Jensen不等式)如果f是R上的下凸函数，则f(W(ξ|G))=E(f(ξ)|G)；

定理2 如果条件期望E[Y|X]以及X的边缘分布已知，则E[Y]=E[E[Y|X]]，Var(Y)=E[Var[Y|X]]+Var[E[Y|X]].

证明E[Y2]=E[E[Y2|X]]=E[Var[Y|X]]+E[(E[Y|X])2]

左边减去E[Y]的平方，右端减去E[E[Y|X]]的平方便可得结论.

2 混合分布

设X,Y均为r.v，I为示性r.v，取值为0和1，其中I=1表示某个事件发生，事件发生的概率为q=p(I=1),0

假设Z代表某个风险保单的理赔支付，则一般有3种情况：

(1)保单合同无理赔，Z=0；

(2)保单合同的索赔额大于最大的保险金额M，Z=M；

(3)保单合同产生正常的索赔额，0

Z的cdf在0和M处各有一个跳跃，跳跃的跨度是Z在该点相应的概率；对于中间部分，用一个连续cdf描述，此时Z的cdf既不完全离散也不完全连续，而是一个离散与连续cdf的混合分布.显然有如下结论：

Fz(z)=P(Z≤z)=

P(X≤z,I=1)+P(Y≤z,I=0)=

qFX(z)+(1-q)FY(z)

Fz(z)-Fz(z-0)=qP(X=z)，

EZ=qEX+(1-q)EY，

mgfmz(t)=qmX(t)+(1-q)mY(t).

值得注意的是，凸组合T=qX+(1-q)Y的cdf并不都具有如此形式.如假定X,Y相互独立且有共同分布N(0,1)，则T～N(0,q2+(1-q)2).又因为Fz(z)=qFX(z)+(1-q)FY(z)=FX(z)，所以Z～N(0,1).显然，T的cdf不具有上述形式.

E[g(Z)]=E[E[g(Z)|I]]=

qE[g(X)|I=1]+(1-q)E[g(Y)|I=0]=

qE[g(X)]+(1-q)E[g(Y)]

如果风险X=IB，I为Bernoulli(q)r.v，B为任意r.v，且I与B相互独立，则

E[X]=E[I]E[B]=qE[B]，

Var[IB]=E[Var(IB|I)]+Var[E(IB|I)]=

E[I2]Var[B]+Var[IE[B]]=

E[I2]Var[B]+Var[I](E[B])2=

qVar[B]+pq(E[B])2

Ms(t)=MN(logMX(t))=

可见S的mgf是常数0的mgf与指数分布的mgf的一个混合.

cdfFs(x)=p+q(1-e-px)=1-qe-px,x≥0，

这是一个在0点有跳度p而其它处为指数型的cdf.

已知混合分布的cdf，如何确定离散型和连续型r.v用来构造混合分布?下面就此问题举例分析[6].

我们首先求cdf的微分形式dFZ(x)，在跳跃点2，4处dFZ(2)=FZ(2)-FZ(2-)=0.5，dFZ(4)=

例2 (有最大保险金额的责任险)考虑承包责任损失为S的保单，免赔额为100，最大理赔支付为1000.即如果S≤100，则保单理赔支付X=0；如果

S≥1100，则X=1000，否则，X=S-100.已知P(

S>100)=0.1，P(S>1100)=0.02，当100

P[B=1000|I=1]=0.02,

P[B∈(x,x+dx)|I=1]=

0.00008dx,0

FX(x)=P(IB≤x)=

P(IB≤x|I=0)P(I=0)+

P(IB≤x|I=1)P(I=1)=

密度函数(pdf)形式为:

例3 (有索赔且索赔服从指数分布)假定风险X有如下分布，P(X=0)=0.5，P(X∈[x,x+dx])=0.5βe-βxdx,β=0.1,x>0，X的均值是多少？对于风险厌恶系数为α=0.01具有指数效用函数的人，愿意为风险X支付的最大保费是多少？

在保险领域，混合分布是常见的一种两阶段模型.通过研究混合分布及其构造形式，讨论如何利用微分法确定混合风险的保费及混合风险的各种统计特征，可以更全面、简便地掌握混合风险的统计规律.

参考文献：

[1]R.卡尔斯,等.现代精算风险理论[M].唐启鹤,等译.北京:科学出版社,2005.

[2]刘嘉锟,王公恕,等.应用随机过程[M].北京:科学出版社,2004.

[3]汉斯U.盖伯.数学风险论导引[M].成世学,严颖译.北京:世界图书出版公司,1997

[4]魏瑛源.混合随机变量的分布[J].河西学院学报,2008,27(02):19-22.

[5]张博.精算学[M].北京:北京大学出版社,2005.

[6]张梅,马建静.微分法在混合风险中的应用[J].内蒙古师范大学学报:自然科学汉文版,2008.37(1).