函数极限中等价无穷小的应用探讨

李 强

（ 铜仁学院 数学系，贵州 铜仁 554300 ）

函数极限中等价无穷小的应用探讨

李 强

（ 铜仁学院 数学系，贵州 铜仁 554300 ）

利用等价无穷小量作代换是计算极限的一种常用、方便、有效的方法。围绕无穷小之比、变上限积分的极限、幂指函数极限和Taylor公式，利用等价无穷小代换思想进行分析应用，以此达到极限求解中化繁为简、化难为易的目的。

等价无穷小； 函数； 极限； 应用

极限的计算方法是多样灵活的，也很有技巧性。其中等价无穷小代换是计算未定式极限的常用方法。但许多教材和工具书对其没有作深入讲解，只是一带而过，致使很多学生对这一概念理解不够，对其应用颇感茫然，更有人不明就里、胡乱套用。如果恰当选择用来替换的无穷小，可以使计算简化，但替换中要严格遵守无穷小替换法则，即下述的定理1。

该定理的证明见参考文献[1]。

定理1说明，无穷小替换只能在商运算中使用。其实不然，下面介绍另外三种用法。

1.无穷小之比

无穷小代换在商式中使用时，必须满足一定条件，否则就会出现错误。比如：究其原因，无穷小代换在商式中使用时，必须满足一定条件，即定理2。

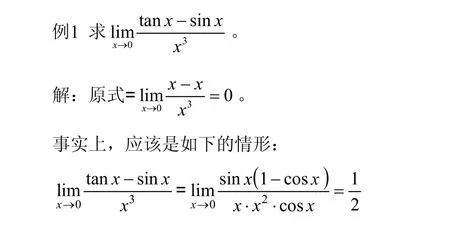
2.变上限积分的极限

常用的变上限积分的等价无穷小有：

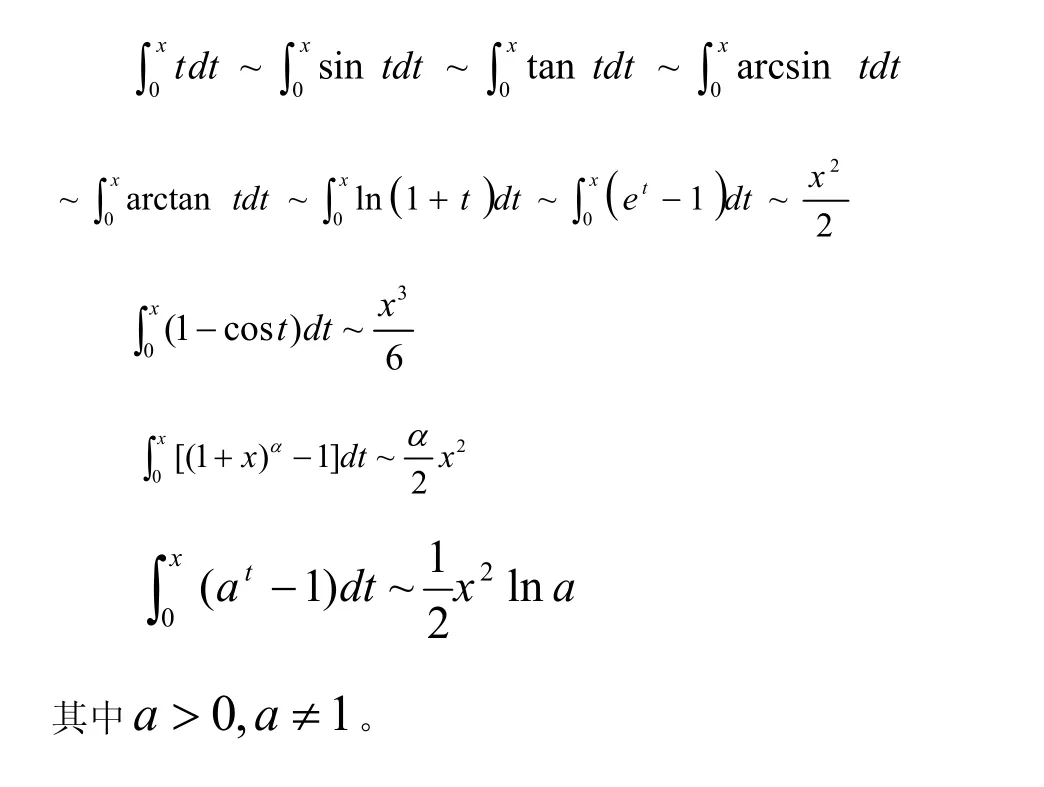
上述等式可以用洛必达法则直接证明，证明中我们可以看到被积函数之间均是等价无穷小，由此可得将被积函数用等价无穷小代换后的变上限积分仍是等价无穷小，即是：

3.幂指函数极限和Taylor公式使用

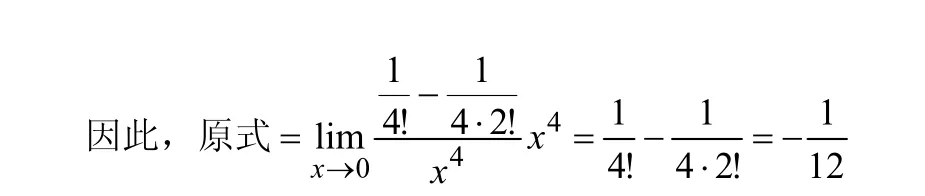
综上所述，我们看到等价无穷小的应用非常广泛，但还是要具体情况具体分析，同时结合洛必达法则，选择合理恰当的方法进行求解。

[1]同济大学数学教研室.高等数学（上册）（第4版）[M].北京：高等教育出版社，2006.

[2]符世斌.幂指函数极限的一种简捷求法[J].高等数学研究，1999，2（3）：20-21.

[3]杨春林，张传芳.变上限积分的等价无穷小[J].高等数学研究，2004（11）.

[4]肖岸纯.等价无穷小性质的理解、延拓及应用[J].数理医药学杂志，2007，20（5）.

Application of the Equivalent Infinitesimal in Functional Limit

LI Qiang
( Department of Mathematics, Tongren University, Tongren, Guizhou 554300, China )

Using the Equivalent Infinitesimal is a common, convenient and effective method to calculate limits. This paper centers on the ratio between polynomials and infinitesimal, the limit of variable upper limit integral and the limit of power-exponent function, as well as Taylor Formula, adapting three kinds of limits and analyzing their application by using the thought of equivalent infinitesimal replacement so as to simplify the process of calculating the limit.

equivalent infinitesimal; function; limit; application

（责任编辑 王婷婷）

O171

A

1673-9639 (2009) 06-0142-03

2009-09-24

李 强（1977-），男，贵州省铜仁市人，贵州铜仁学院数学系讲师。研究方向：数学教育。方程。