纳什平衡的计算问题

许道云

（ 贵州大学 计算机科学与技术学院，贵州 贵阳 550025 ）

纳什平衡的计算问题

许道云

（ 贵州大学 计算机科学与技术学院，贵州 贵阳 550025 ）

本文介绍了博弈的形式描述系统，混合博弈实质上是基于纯博弈系统框架下在策略集上引入概率分布。局中人之间的不合作性表现分布之间的独立性。给出了囚犯二难概型博弈系统与其纯博弈系统纳什平衡之间的联系，并对概率纳什平衡的计算进行了讨论。

纯博弈系统； 离散概型博弈系统； 纳什平衡； 支付计算

博弈论的产生背景主要源于经济学中经济行为冲突的量化分析与行为推断[1]。随着不同博弈系统（模型）的提出以及在其它领域的应用，人们开始注意到：博弈论的应用不仅局限于经济领域。除了经济学家以外，数学家和计算机科学家对博弈论的基本理论、数学描述、应用联系展开了更加深入的研究。如：参考文献[2]用非线性分析方法对纳什平衡的存在性及性质展开系统研究，参考文献[3]则将纳什平衡与（优先）逻辑程序的回答集相联系，等等。

我们感兴趣如下问题的研究：

（1）博弈论中的一些思想和结论在布尔公式可满足性问题（SAT问题）、以及在一般约束可满足性问题（CSP问题）中的联系和应用。

（2）弱纳什平衡问题。混合博弈（本文称概型博弈）的纳什平衡总是存在的。但是，纯博弈的纳什平衡不一定存在。而由一个纯博弈系统可以诱导出一个概型博弈系统。一种自然的想法是：如果一个纯博弈系统的纳什平衡不存在，如何从对应的概型博弈系统的纳什平衡近似决定原系统的近似纳什平衡（称为弱纳什平衡问题）。

（3）纳什平衡判定问题。纯博弈的纳什平衡不一定存在。于是自然有如下判定问题：

NE问题（Nash Equilibrium Problem）：

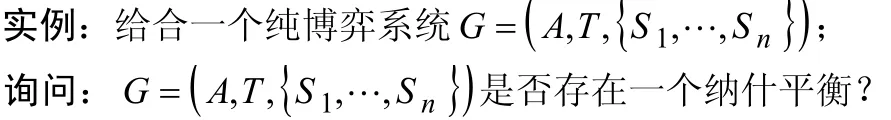
NE问题应该是一个NP-完全问题。

我们关心的是：哪种类型，或在何种充分条件下，纳什平衡必然存在？

（4）计算纳什平衡（如果存在）的有效算法及计算复杂性。

基于上述动机，本文首先给出了博弈系统的形式描述，提出了概型博弈系统的概念，并指明通常的混合博弈实质上是基于一个纯博弈系统框架产生的扩展系统，博弈中的不合作性表现为分布之间的相互独立性。这些有助于理解两类系统之间的联系，以及概率论方法在研究博弈论中的应用。基于此，概率论的工具可以用于讨论更复杂的博弈系统（如：连续型博弈系统等）。其次，我们对一个典型的概型博弈系统的纳什平衡的性质及其计算方法作了进一步的探讨和研究。

1.博弈论基础知识

例1 （囚犯二难问题）

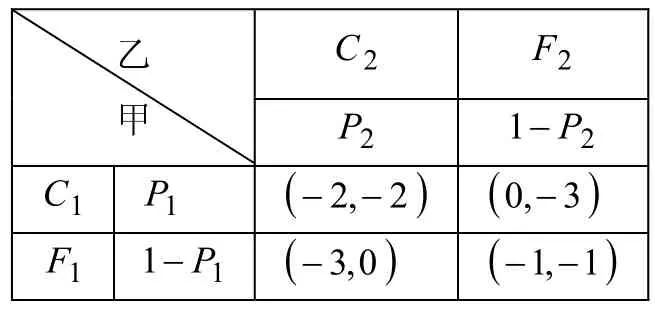
设有甲、乙两人共同犯罪，被囚于不同房间。两人都知道获刑规则：如果两人都坦白，各被判2年监禁；如果两人都保持沉默（抵赖），各被判1年监禁；如果一个坦白，另一个抵赖，坦白者可以释放，抵赖者被判3年监禁。甲、乙之间进行博弈，如何选择自己的策略，才能使被监禁时间最短。

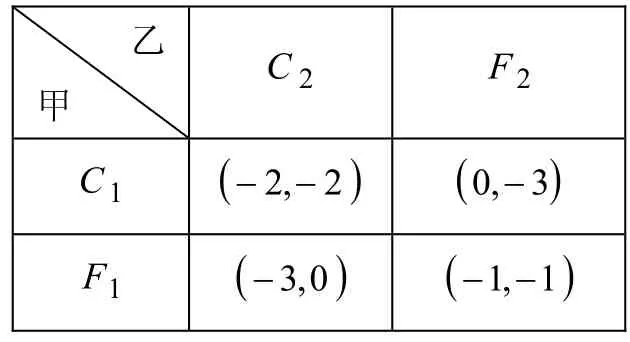
乙甲C2 F2 C ( )2 1− ( )3 2,−0,−F ( )0 1− ( )1 3,−1,−

请注意：纯博弈系统的纳什平衡可能不存在，即使存在，也可能不唯一。

自然地，我们会提出如下两个问题：

（1）纳什平衡的存在性判定问题；（2）如果纳什平衡存在，如何计算？

对于问题（1），我们建立如下判定问题：

NE问题：

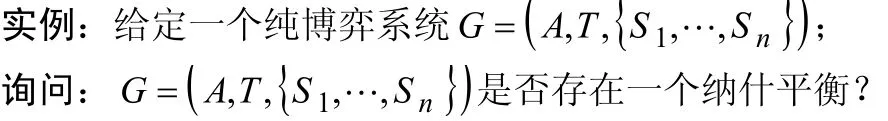
2.离散概型博弈系统

在纯博弈系统G=(A,T,{S1,…,Sn})的基础上，我们考虑在策略集上引入一个概率分布，从而引入离散概型博弈。通常称为混合博弈（参见参考文献[1]和参考文献[2]）。

我们在此称为离散概型博弈，是因为在离散策略集上引入了概率分布，从如下的讨论将会看到：形式上我们将以概率分布代替策略先择，以分布下的数学期望表示支付。

例2 （囚犯二难问题对应的概型博弈）

（1）以例1中的纯策略博弈系统为基础框架。在策略集上引入概率分布。

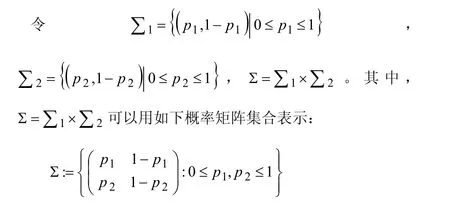
信息表T可以改写为：

乙甲 P2 1−P2 CF2 2 CP1 ( )2 1− ( )3 2,−0,−F1 1−P ( )0 1− ( )1 3,−1,−

A B CF2 2 C ( )b 1−, ( )d b− − a ,−F ( )a 1− , ( )c d− −c,−

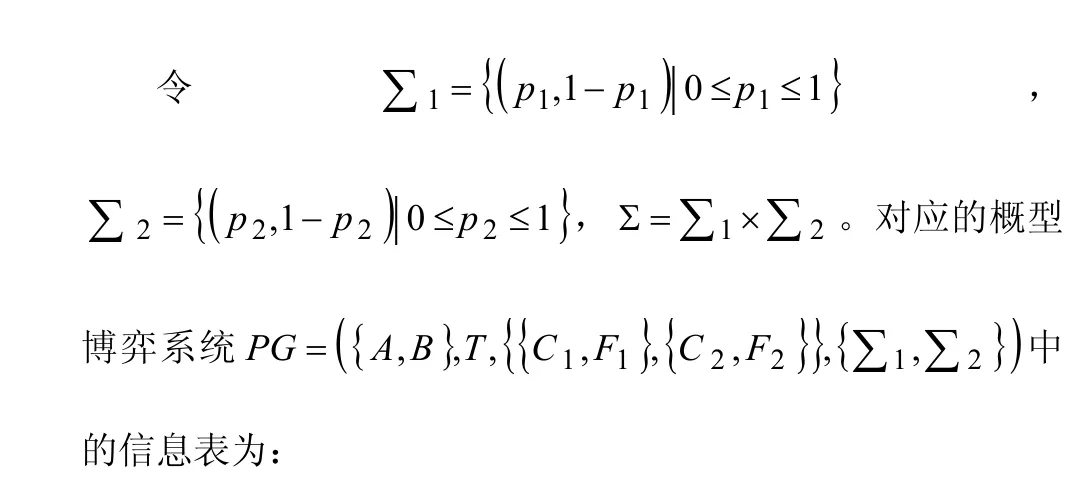
B AP2 1−P2 CF2 2 CP1 ( )b 1−, ( )d b− − a ,−F 1−P1 ( )a 1− , ( )c d− −c,−

信息表T为：

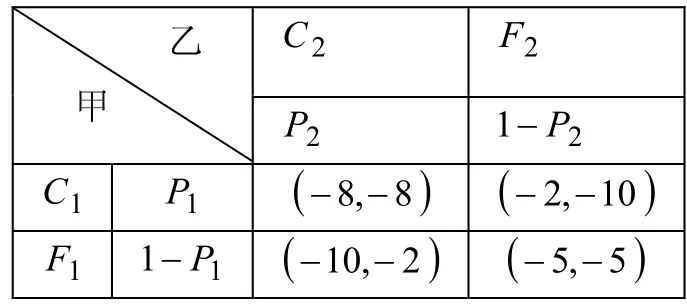
乙甲 P2 1−P2 CF2 2 CP1 ( )8 1− ( )10 8,− −2,−F1 1−P ( )2 1− ( )5 10,− −5,−

3.双人概型博弈系统

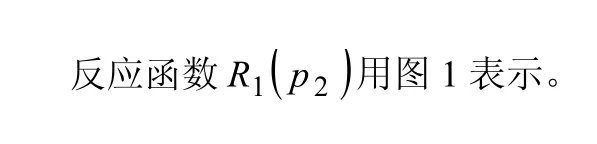
图1 反应函数 R1(p2)

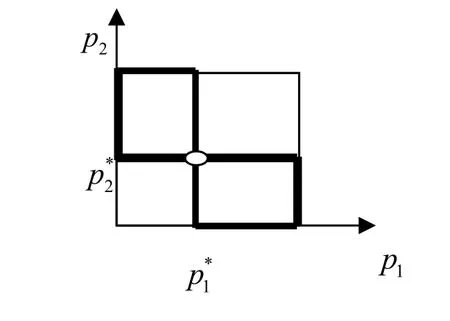
图2 两个函数合并图

两个函数的合并用下图表示：

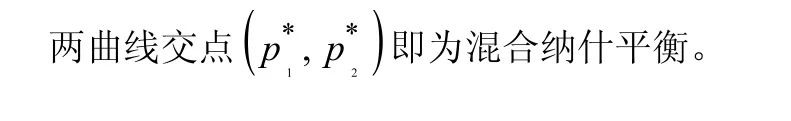
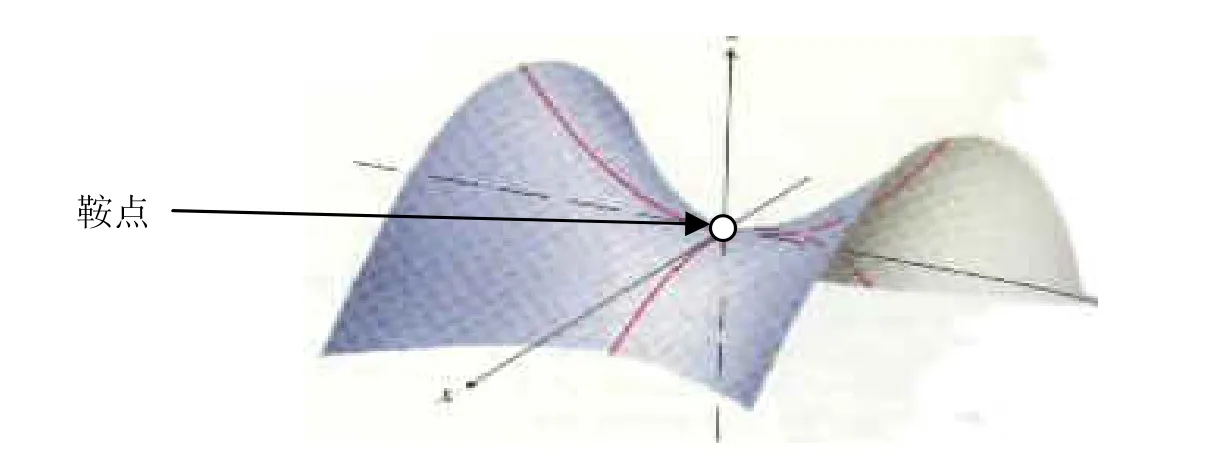
图3 鞍点

纳什平衡几何上表现为三维空间中曲面的“鞍点”。从下图看出："鞍点"表现为一个稳定点。

本文首先给出了博弈系统的形式描述，混合博弈实质上是基于纯博弈系统框架下在策略集上引入概率分布。局中人之间的不合作性表现分布之间的独立性。这有助于理解两类系统之间的联系，以及概率论方法在研究博弈论中的应用。此外，我们还对一个典型的概型博弈系统的纳什平衡的性质及其计算方法作了进一步的探讨和研究。

[1]张维迎.博弈论与信息经济学[M].上海：上海三联书店，上海人民出版社，2004.

[2]俞建.博弈论与非线性分析[M].北京：科学出版社，2008.

[3]N. Foo, T. Meyer, and G. Brewka. LPOD answer sets and Nash equilibra[M].. Avvance in Computer Science, 9thAsian Computer Science Conference, LNCS 3321: 343-351,2004.

Calculation of Nash Equilibrium

XU Dao-yun
( College of Computer Science and Technology, Guizhou University, Guiyang, Guizhou 550025, China )

This paper describes formal-description system of the game; mixed game essentially means introducing probability distribution to strategy sets based on the framework of pure game system. Non-cooperativeness among players shows the distribution independence. It gives the connection between prisoner’s dilemma scheme game system and Nash equilibrium of pure game system, and makes a discussion on the calculation of probability Nash equilibrium.

pure game system; discrete scheme game system; Nash equilibrium; payment calculation

（责任编辑 王婷婷）

TP301.5

A

1673-9639 (2010) 01-0131-08

2009-01-19

贵州省优秀科技教育人才省长基金。

许道云（1959-），男，博导，教授，主要研究领域为计算复杂性，可计算分析。