在“问题”的深层挖掘中培养学生的创新精神
2009-10-23梅兆全
梅兆全
新课程标准提出:通过义务教育阶段的数学学习,使学生具有初步的创新精神和实践能力。课程改革以后,由于教材的变化,教师不再是教教材,而是用教材教学。新教材中出现的问题,大多和学生的生活实际有着密切联系,有些问题学生既感到有趣,又觉得难以下手。教师教学时要善于教会学生找准切入口,分解问题,理清思路,逐层深入,让学生在问题的深层挖掘中灵活地自我提问,自我解决,让学生在实践中寻找乐趣,体现价值。
义务教育课程标准实验教材三年级(上册)第13页有一道练习题:42个小朋友集中去公园游玩,坐小船每条5元,坐大船每条6元,大船限乘4人,小船限乘3人,你准备怎样租船?这道题是在教学了一位数除两位数的除法以后编排的,自然和除法有一定的联系。教学时我引导学生分步提问,逐层深入。
首先解决怎样乘船的问题。学生通过讨论可以提供两种方案。方案一是全部乘大船,列式为42÷4=10条……2人,结果要租11条大船;方案二是全部乘小船,列式为42÷3=14条,结果要租14条小船。在肯定了学生提供的方案的正确性的基础上,告诉学生这样解决问题的思路是单一的,既不能锻炼自己解决实际问题的能力,也不能涵盖教材的编排意图。由此再引导学生讨论第二个问题:是否可以大、小船同时租呢?聪明的学生在老师提出问题以后,很快发现了可以将方案一进行修改,可以让40人乘10条大船,余下的2人乘1条小船。此方案出来以后,学生发现了可以用小船换大船,所以立即又有学生提出了,2人坐一条小船,还有一个空座位,所以还可以增加一条小船,减少一条大船,即可以租9条大船,2条小船。
教者适时点拨,提示学生可以先假定大船的条数,再根据乘船人数计算出小船的条数。学生计算以后得出了多种不同方案,教者帮助学生将乘船方案列成表一:

讲到这里,不同的租船方案都有,似乎这道题的讨论可以结束了。然而一个新的问题又激起了同学们热烈的讨论。在以上各种方案中,到底哪种方案最好呢?大家都知道谁的方案租金最少,谁的方案就最好。那么怎样计算租金呢?又需要什么条件呢?学生这时回过来看书才发现,原来坐每条小船5元和坐每条大船6元,是用来计算租金的必要条件。根据这一条件,学生很快可以口算出不同方案所需要的租金。将同学们口算的结果填入表二。
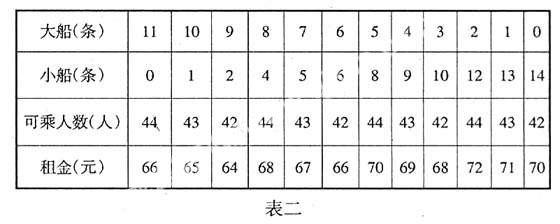
通过观察比较,学生很快确立了最佳租船方案:既要尽可能多乘大船,减少租金,同时又要尽可能使每条船都没有空位置,这样才能使租金最少。这样的教学活动既充分调动了学生的学习积极性,又使学生的创新精神在实践活动中得到了锻炼和培养。
作者单位:扬州市邗江区李典学校
