组织好两项活动 促进学生自主建构

傅建霞

由于数学知识的抽象性和小学生思维的形象性之间存在着矛盾，所以小学生在理解抽象的数学知识时，常常是勉强知其然，很难知其所以然，实际运用时稍有变化就会不知所措，从而使数学课堂教学的效果很难令人满意。随着新一轮课程改革的实施，如何运用新理念来改善数学教学的方法，努力解决好这一对矛盾，增强数学学习的效果，这是每一位数学教师关心并思考的问题。下面结合教学实践谈一谈我们的认识和做法。

一、积极引导学生“亲自做”，获得深刻的数学体验

建构主义理论认为，儿童数学学习的过程是建立在他们校内、校外经验基础上的一个主动建构的过程。要使课堂教学能够促进学生有效学习的进行，必须重视学生“主动建构”的必要条件和主要过程。“做”是指学生运动产生问题后，在教师的帮助下，自己动手、动脑尝试着解决问题。由于数学具有高度的抽象性，学生只有通过亲自“做”，才能对数学材料、数学事实等获得深刻的认识和体验，为“主动建构”创造必要条件。因此，“亲自做”是学生理解、掌握数学知识的必要活动，课堂上教师应积极引导学生亲自做。由于学生年龄小，“做”的能力还很弱，教师要注意加强指导，帮助学生借助合适的方法，亲自“做”成功，从“做”中获得正确的、深刻的数学体验。

1动手操作。研究表明，小学生对数学的体验主要来自于动手操作。在学习抽象的数学知识时，我们尽可能地引导学生去操作。借助操作，让学生获得丰富的深刻的数学体验，为理解抽象的算理、发现数学的内在规律铺路搭桥。例如，学习圆周率这一内容时，我们首先让学生测量一些圆的周长与直径或半径，并让学生求出周长与直径或半径的比，通过这一系列的探索活动学生就能很快发现，圆周长与直径或半径之间的比总是3倍或6倍多一点，然后再引出圆周率。虽然这样做不如教师直接告知学生简单省时，但却为后面真正理解、掌握圆周长的计算方法及灵活运用周长的计算方法解决实际问题奠定了坚实的基础，增强了学习效果。

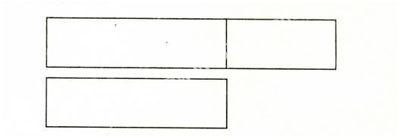
2建立模型。有些数学知识抽象程度比较高，学生在学习这类知识时，常常借助直观能够理解和运用，一旦离开直观就无从下手。由于课堂教学的时间有限，不可能一直让学生借助直观解题。因此在加强实际操作积累感性经验的基础上，还要注意引导学生利用简单明了的直观图，在头脑中构建数学模型，让他们在一段时间内能够借助数模解决问题。如教学求比一个数多几的数的应用题时，首先让学生借助操作领会大数可以分成两部分，一部分是和小数同样多的，另一部分是比小数多的。接着引导做“例题”，开始建模，即一边引导学生分析：哪个多，哪个少?多的可以分成哪两部分?一边根据学生的回答相应的画出长条图：

然后引导学生借助长条图弄清要求的数是两部分的和还是一部分，从而确定算法。后面的“想想做做”，在引导学生分析哪个多，哪个少，多的可以分成哪两部分时，教师都要相应的指长条图。通过说和指，促使比较数量多少的过程与长条图有机结合起来，使黑板上的直观图变成学生头脑中这类数量关系的模型。当离开直观图解题时，随着两个数量的比较，学生头脑中就会出现这一长条图，从而顺利找到解题思路，为抽象概括这类应用题的数量关系积累丰富的活动经验。

二、适时引导学生“悉心悟”，把握抽象的数学规律

通过“做”，学生已初步获得了对新知的认识，但这些认识只是具体的、零散的、浅层次的。如不适时进行抽象概括，自主建构，学生将永远停留在感性认识的层面上，难以摆脱对具体形象的依赖，解决问题的效率和解决问题的能力会受到严重影响，抽象思维能力得不到提高。因此，在引导学生“亲自做”的基础上，教师还要重视引导学生在不断的体验中，悉心地“悟”，适时建构，顺利完成认识上的飞跃。因而，“悟”是学生真正理解、掌握数学知识的关键性活动，是学之道。由于“悟”非外部活动，学生往往难以把握，教学中教师要根据教学内容和学生的特点，采用合适的方式，适时地加以引导。

1址“做”边“悟”式。对于抽象程度不太高的数学知识，在学生“做”时或“做”后，我们及时引导学生对做的过程、结果及其中出现的现象等进行反思，帮助他们将新知识在头脑中逐步完善、丰富和系统化，顺利建构。如认识长方形和正方形，先让学生折一折、量一量，发现并及时概括出长方形和正方形的特征；然后再让学生找图形，先找出所有的长方形，再找出所有的正方形，结果发现，大多数学生找出的长方形中包括正方形，有的同学找出的长方形中不包含正方形，立即反问：“这是怎么回事?”学生通过反思，及时悟出长方形、正方形的特性，从而形成完整的认知结构。

2“水到渠成”式。对于抽象程度比较高的数学知识如数量关系、算理等，我们先让学生借助操作和数模去“做”，获取广泛的深刻的活动经验。在学生积累了丰富的数学活动经验的基础上，再引导他们对所学的新知进行比较，通过异中求同，帮助学生悟出新知中蕴藏的规律性的东西，从而顺利摆脫直观形象的束缚。如教学求比一个数多几的数的应用题时，先引导学生借助长条图做“例题”及“想想做做”，顺利地找到算法。在他们借助数模积累了一定的解题经验后，再引导学生将做过的题目进行比较，说一说为什么都用加法算?学生借助数模和解题经验，不仅很快明白“大数可以分成两部分，求大数，就要将两部分合起来，用加法算”，而且此后就会自觉运用这一规律去解题，顺利完成向抽象思维的飞跃。

3“一点即通”式。有些数学知识很难让学生有具体直观的数学体验如运算定律、性质等，要让他们悟出其中之道就更难。对于这类知识，我们可以根据数学来源于生活及与世间万物都是有联系的观点，采用打比方的方法，借助学生在生活中经历过的、印象较深的事情，以简单明白的事理来说明抽象的数理，通过两者之间的共通性促进学生对这类知识的理解和感悟。如教学角的初步认识时，由于学生在生活中见到的角都是跟面联系在一起的，因此很难真正理解“角的大小与边的长短无关”。当让学生比较度数相同、边的长度不同的两个角时，意见发生了分歧，有的学生认为一样大，有的学生认为是第二个角大。我未作评判，先让他们分别说说是怎么比的。持第二种意见的同学认为第二个角上端两边叉开得大些，我边听边点头说：好像也有道理。随即请班上最瘦小的一位同学起立，让其他同学来比一比老师和这位同学的手臂，谁的粗?在大家一致认为是老师的手臂粗后，我却说是这位同学的手臂粗，并当众将自己手腕处和学生的大臂处进行了比较，证明我的结论是正确的。这时所有的同学都大叫：不公平，不是比的同一处。此时我顺势而上：你们刚才比较两个角的大小时是比的同一处叉开的大小吗?持第二种意见的同学顿时不好意思地笑了起来。这时再用多媒体将两个角重叠，并把角的两条边不断地延长，使学生清楚地看到两个角同一处叉开的大小始终一样，从而真正明白“角的大小与边的长短无关”。没想到通过多种方法都没能让学生真正明白的道理，在此只借用了“比手臂粗细”这件事，就使学生茅塞顿开。

学习是一个主动建构的过程。我们只有遵循儿童的认知规律和数学学科的特点，抓实“做”和“悟”这两个环节，才能把握好形象与抽象之间的平衡度，从而促使学生顺利完成自主建构过程，真正提高数学课堂教学的有效性。