“基本数学经验”的教学利用与思考

杨　玲

在学习数学的过程中，由对数学知识的认识而产生的一些体验和意识的积累，就会渐成为一种经验——基本数学经验。这种经验在教学中如果能得到充分利用，就能更加有效推进学生的数学学习。

一、“基本数学经验”的教育价值

1“基本数学经验”为学生掌握基本数学知识，形成数学技能，学会数学方法夯实基础，起铺垫作用。

学生对于新知识的认识和理解必须通过已有经验，将新旧知识联系，并进行内化，达到形成新的经验和技能的目的。

在小学阶段，学生已经积累的数学经验，对于学习新的知识，形成新的技能，体会数学思想方法都有着桥梁和铺垫的作用，不可忽视和忽略对经验的积累。

2“基本数学经验”密切了数学与生活的联系，为学生解决实际问题再现了现实情境。

[案例广小数乘法中求积的近似值”教学片断

情景导入：老师逛超市时，发现大米优惠销售，优惠价是每千克2.74元，老师买了5.7千克。一共用了多少钱?

师：怎样列式?

生：2.74×5.7=

师：你能快速算出结果吗?

生在练习本上计算，老师巡视，然后指两生板演(竖式略)：

生1：2，74×57=15.618(元)

生2：2.74×5.7=15.618(元)≈15.62(元)

师：两位同学横式后的结果不一样，谁的更合适?为什么?

小组讨论。

生3：我认为第二个同学的答案更合适，因为超市结账时的小票就是两位小数，没有三位的。

生4：我也认为第二个同学的答案更合适，因为人民币的最小单位是分，没有比分更小的单位。

显然，两位学生的认识都來自于生活经验，学生用自己逛超市使用人民币的经验来解释数学问题，这个过程就是生活经验转化为数学知识和数学活动经验的过程。

3“基本数学经验”提倡内省，突出个性化，促进学生把握数学的本质和意义。

[案例广平行线”教学片断

师：请大家在纸上任意画两条直线。

生在纸上画，老师巡视。

师：你能根据两条直线的关系，把你画的图形分分类吗?

小组合作继续探究。

生、：我们组是这样分的：①②③不相交的分在一组，④相交的分在一组。

生2：我们组是这样分的：②不相交的分在一组，①④相交的分在一组，③延长后重合的分在一组。

生3：我们组是这样分的：②延长后也不相交的分在一组，①③相交或延长后相交的分在一组。

师：①②为什么不放在一组?你们为什么认为①组两条直线是相交的?③为什么不和①④放在一组?

生争论……

在这一环节，学生自主探究时，个性化的经验决定了不同的思路，而个人的思维又左右着小组同伴的想法，大家通过内省产生争论，在争论中促进思考，逐渐统一了认识。

二、“基本数学经验”的教学利用与思考

1在经验申建立几何概念，发展学生的空间观念，培养想象力。

[案例尸体积和体积单位”教学片断

一上课，教师把两个大小一样形状完全相同的杯子放在讲台桌上，向里面倒了同样多的水(见图一)。

师：这两个杯子一样大，里面装了一样多的水。

(老师把一个小球皮放进其中一个杯子里)

师：你们看见了什么?

生1：老师您把一个小球放进一个杯子里。

师：仔细看，还发现了什么?

生2：我发现杯子里的水面升高了。

师：那是不是说明这只杯子里的水多呢?

(生纷纷摇头表示否定)

师：那是为什么呢?

生2：小球放进去后占地方，就把水挤上来了。

老师又把一个大球轻轻放进另一个杯子里(见图二)。

师：这次你又发现了什么?

生：把大球放进这个杯子，水面上升得更高了，超过了另一个杯子(见图三)。

师：你知道这是为什么吗?

生：这是因为大球比小球占的空间大。

本环节教师从生活中找到了研究体积的切入点，使学生在轻松、愉快的课堂气氛中，对体积的意义有了非常感性的认识：物体不仅要占据空间，而且占据的空间有大、小之别。

2在经验申理解算理优化算法，提高学生的计算能力，培养良好数感。

[案例]“一位数乘两位数”教学片断

师：看下图，每头大象搬了多少根木头?

你是怎么知道的?

生1：我先数一堆是10根，两堆就是20根。

生2：我用10×2得到20根。

师：想得都很好，那么3头大象一共运来少根木头?你能用算式表示吗?

生2：我用20×3。

生4：我用3×20。

生5：我用20+20+20。

师：三个同学都不简单，列出了三道算式，今天我们来研究前两种方法。那20×3等于多少呢?

生1：我用20+20+20等于6。根。

生2：我是看图上有‘堆，每堆10根，就是60根。

生3：我先想“二三得六”，再添上。就是60。

师：你这种方法有意思，想乘法口诀“二三得六”，那后来添。是什么意思?

生4：我是先不看这个0，乘出来后再添上。

师：噢，你是先不看0，先算2个十乘3得六个十，就是六十，所以要在6的后面添ho，对吧?非常好!

显然，学生能充分利用已有的知识经验——整数加法以及一位数乘一位数的口诀，不仅正确列出算式，而且想出了算法。由于题中有图，学生自然而然地又联想到图意，想到“6堆，每堆10根，就是60根”，这种将数与形有机结合的经验帮助学生理解了算理。在得出不同算法时，自然有所比较，优化了方法，得出了乘法的简便性。

3利用数学活动经验收集和处理数据，掌握统计和概率知识。

新的数学课程加强了对统计知识的教学，《数学课程标准》明确指出，要让学生“掌握统计和概率的基础知识和技能，并解决简单的问题”。也就是说，学生需从事一定的数学活动，在活动中认识到统计与现实生活的联系，在经验中掌握统计的知识与技能，获得必要的思维训练。

例如，六年级上册实践活动课“算出它们的普及率”。

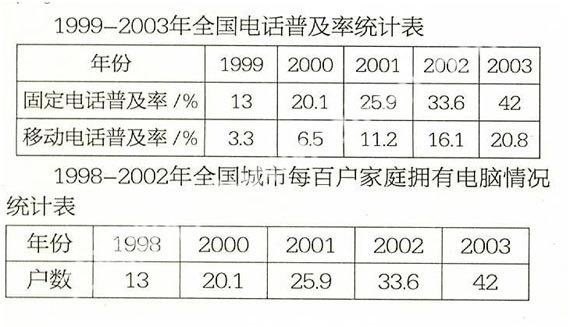
1999-2003年全国电话普及率统计表

1998-2002年全国城市每百户家庭拥有电脑情况统计表

小组讨论：

(1)电话和电脑的普及率哪一个高一些?你们调查统计的结果能反映本地区电话、电脑普及情况吗?为什么?

(2)通过这次调查活动，你有哪些体会?

以上的学习过程，最大限度地体现了学生运用已有知识经验和生活经验来解决实际问题的方法，学生在活动中通过讨论体会了统计结果的意义，增强了应用意识。

4别用数学经验寻求解题策略，提高实践与综合应用能力。

现行的苏教版教材，关于解决问题的策略内容安排得比较丰富，它满足了学生在数学知识应用上的需求。

例如六年级上册“鸡兔同笼”是安排在例题2后的练习中，问题如下：

“鸡和兔一共有8只，数一数腿有22条。你知道鸡和兔各有多少只吗?”

因为有了例2的知识基础，本题教师采用分组讨论交流的形式，要求学生可以用不同的方法寻求解题思路。学生在4人一组的学习环境中，充分发挥了自主能动作用，想出不同的解题方法，包括本课新学的假设法，以前的画图法，还有列方程法。

解法一：画图法。分两步，第一步把8只都看成鸡，画8个头，每只2条腿，一共画16条腿。(如下图)

第二步发现22-16少了6条腿，因为兔有4条腿，在1只鸡上添上2条腿，使之变成1只兔，一共添2个2只，所以有3只兔，那么有鸡8-3=5(只)。(如下图)

解法二：假设法。先假设8只都是兔，那么一共有腿8×4=32(条)，多出了32-22=10(条)，每减少2条得到1只鸡，所以一共有鸡10÷2=5(只)，兔有8-5=3(只)。

解法三：列方程法。解：设鸡有x只，那么兔有8-x(只)。

解得鸡有5只，兔有3只。

学生通过不断反思，不仅学会运用替换和假设的策略分析数量关系，确定了解题思路，有效解决了问题。同时，在已有的数学经验——画图策略和方程知识的基础上，还想出了不同的解题方法。在寻求解题策略的过程中，学生进一步积累了解决问题的策略意识，提高了实践与综合应用能力。

在数学教学中，教师要善于将生活经验转化为学生“火热”的思考，进而形成和积累“基本数学经验”，让学生涌动激情，从中体验学习成功的快乐，真正达到顺缕成帷、水到渠成的境界。