迁移能力培养下的小学主题单元教学

随着时代的发展，“运算能力”作为核心素养被提出来，它的意义不再仅仅局限于简单的计算技能，而是追求对运算背后知识、方法、思想、原理的理解。核心素养下的数学运算被赋予了更多维度的要求和更深层次的内涵。

苏教版教材中整数乘法教学始于二年级上册第三单元“表内乘法”，止于四年级下册第三单元“三位数乘两位数”。在这期间，三年级上册安排“两、三位数乘一位数的笔算（含估算）”，三年级下册安排了“两位数乘两位数”。每个单元学习内容相互关联、层层递进，进一步分析，可以将整数乘法分为两个层次进行教学，第一层次是乘法的意义及表内乘法；第二层次是多位数乘一位数、两位数乘两位数和两位数乘三位数，目标是运用分与合的思想迁移运用表内乘法相关知识进行计算。

“两位数乘两位数”属于整数乘法第二层次教学内容，在笔算乘法中具有承前启后的重要作用，有着与两、三位数乘一位数相同的口算算理和算法，又是笔算教学中的一个转折点，即从以前的“一层”跨入了“两层”，也是四年级下册“三位数乘两位数笔算”教学的一个正迁移。教学时可以通过迁移运用多位数乘一位数的相关知识来解决两位数乘两位数。但在以往单课时的教学实践中，笔者有这样的感受：“只见树木，不见森林。”即不仅忽视了不同阶段笔算学习之间的内在关联性，而且没有从乘法的意义、算理等高位视角进行整合。因此，学生在缺乏联系的点状学习中难以迁移运用已有知识结构解决问题，导致迁移能力的培养未能达到预期效果。这种现象不禁让人反思，能否以相同的算理和算法作为迁移点，以单元主题教学的形式，帮助学生构建笔算乘法的整体知识，培养学生的运算能力和推理能力呢？这就是笔者研究“两位数乘两位数”主题单元教学想要突破的。

一、促进迁移能力培养的数学主题单元教学

在新知识的初学阶段，其意义的建构和获得还没有真正完成。按照有意义学习理论，新旧意义之间的联系有一个同化、迁移的过程。所谓迁移，就其字面意思而言，就是搬动、转移；从心理学视角来说，是指一种学习对另一种学习的一个影响。在学习活动中，迁移能力的培养与形成至关重要。具备迁移能力意味着学生能够通过已学过的知识，寻找到前后知识之间的关联性，将未知问题转化为已知问题来解决，并能做到举一反三、灵活运用。这一能力对于提高学生自主学习效率具有积极的促进作用。主题单元教学以知识结构为线索，以落实素养为根基，以促进意义理解和实现迁移运用为目的，通过结构化和整合化的教学活动，促进学生深度学习，同时深化学生对单元主题的理解和掌握。

二、学生迁移能力现状分析

学情分析是主题单元教学的逻辑起点。为了了解学生的迁移能力，笔者对所带两个班级90名学生进行了前测：想一想，24×12的意义是什么？怎么计算？尝试将你的计算方法表示出来。该题侧重对以下两方面内容进行分析：（1）学生能否将多位数乘一位数的算理和算法经验迁移运用到两位数乘两位数的运算中。（2）若无法迁移，学生计算时的主要难点是什么？需要教师如何进行指导？

（一）学生的迁移能力

前测结果显示，17%的学生计算过程和结果完全正确，10%的学生只有结果；22%的学生无论用横式还是竖式计算时都出现了共性错误：24×12=2×24＋1×24=72，这种算法是学生受到了多位数乘一位数的影响，忽略了中间交叉乘积的计算，其根本原因是不理解两位数乘两位数的本质；50%以上的学生虽然能够理解乘法算式的意义，并能借助点子图进行表征，但对两位数乘两位数的算理和算法却无法用准确的语言进行表述，如先算什么、后算什么，更无法提炼两位数乘两位数的算法规律。

（二）学生的难点分析

将24×12的运算过程进行分解：首先是2×4等于8，然后是2×2等于4，当然是40，接下来是1×4等于4，也是40，最后是1×2等于2，然后再将它们相加。这里存在五个步骤，哪一步是学生的学习难点呢？从调研数据来看，学生对个位数上的2×4、2×2的计算基本没有困难，这是之前学过的一位数乘一位数的计算；学生真正的计算难点在于12中十位上的1×4为什么是40，而且在列竖式时为什么要从左下方往右上方去乘，且这个4的书写位置为什么对应的是十位，而不是个位。这也是学生计算两位数乘两位数频繁出错的点。这个难点的根源在于学生对算理的不理解。竖式计算从以前的一层跨入现在的两层，怎样突破这个难点，也是笔者本次教学研究的重点。

三、以迁移能力培养重构单元教学内容

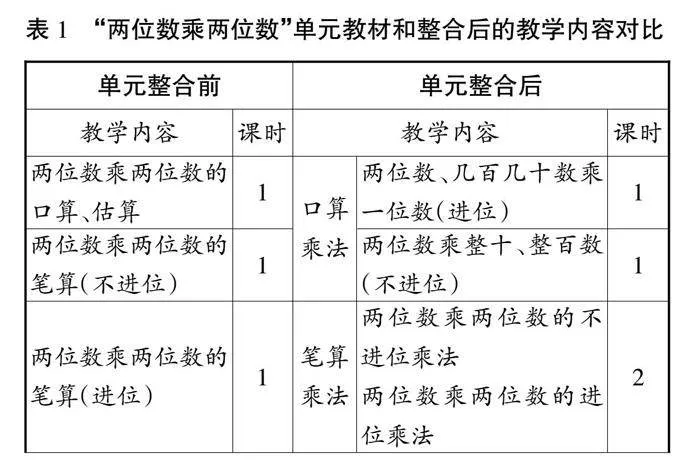
基于以上分析，笔者尝试以培养学生的迁移能力为主线，对教材内容进行整合，以“多位数乘两位数”为单元主题，将两位数乘两位数的口算、笔算融入其中，让学生经历算理探究和算法归纳的全过程，发展学生的运算能力，并迁移运用到多位数乘两位数的运算中（见表1）。

重构后的主题单元教学将笔算乘法作为核心内容，同时联结了四年级下册第三单元“三位数乘两位数”的计算，通过4个课时的教学，帮助学生沟通笔算与其他算法之间的联系，并将两位数乘两位数的算理和算法迁移运用到多位数乘两位数的计算中，从而实现迁移能力的培养。

四、基于迁移能力培养的主题单元教学过程

基于迁移能力的培养，笔者在这里重点对口算乘法和笔算乘法两个板块教学活动的设计进行论述。

（一）口算乘法，回顾乘法运算算理

1.激活经验，回顾乘法意义和两位数乘一位数算理

任务一：出示情境图，李叔叔买了2盒草莓，每盒草莓14个，一共有多少个草莓？自主列式，说一说为什么用乘法，14×2表示什么，14是由什么组成的。

学生活动：大部分学生能够列出算式14×2或2×14，表示的意义都是2个14是多少，只有极少部分学生会列出14+14。

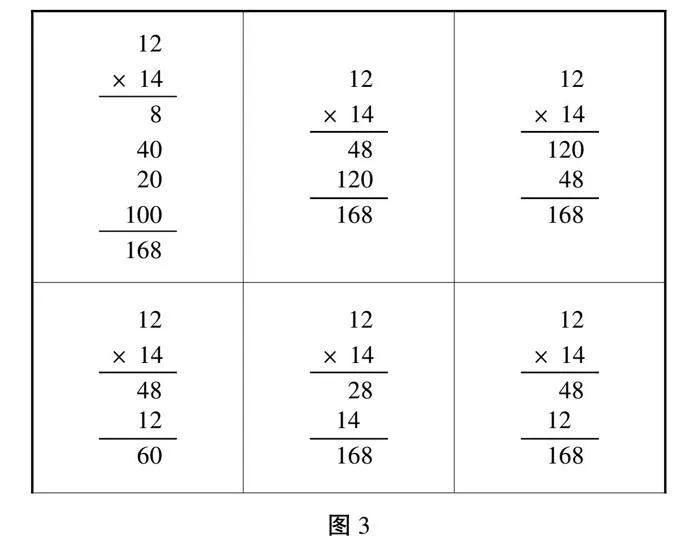
教师提问：你能口算出14×2的结果吗？并解释自己的口算方法。这些口算方法各自有什么特点？说一说你喜欢哪种口算方法。（见图1）

（设计意图：这一环节从乘法的“零认知”出发，根据情境图列算式，引导学生回顾乘法的意义和数的组成，奠定乘法的基础知识，明确“先分后合”的计算思路，为新知学习打好基础。）

2.自主探究，感悟从未知到已知的转化过程

任务二：出示情境图，李叔叔培育出一批新品种菜椒，送给敬老院10盒，每盒12个。一共送给敬老院多少个菜椒？12×10的结果是多少呢？

生：利用一位数乘两位数的计算方法进行口算，把10盒分成9盒和1盒进行计算，12×9＝108，12×1＝12，108＋12＝120（个）。

生：我把每盒的12个菜椒分成10个和2个进行计算。10×10=100，2×10=20，100+20=120（个）。

生：把10盒分成2个5盒，先算5盒有多少个，再算2个5盒有多少个，12×5=60，60+60=120（个）。

教师提问：对比分析，这些口算方法，你最喜欢哪一种？它们有什么共同点？

显而易见，三个学生都迁移运用了两位数乘一位数口算中“先分后合”的计算思路。这样一拆分就把两位数乘两位数转化成了原来学过的两位数乘整十数和两位数乘一位数。

生：这样太麻烦，我利用学过的一位数乘整十数的方法进行口算，直接算12×1等于12个一，12×10就等于12个十，也就是120。

追问：计算12×10，为什么可以先用12×1，然后再添0呢？道理是什么？

学生小组讨论。小组讨论结束后，师生共同总结算理：口算两位数乘整十数时，先把0前面的数相乘，然后再把0添上去。特殊的，对于几十乘几十时，先算几乘几，再添两个0。

（设计意图：对于乘法口算而言，在计算时最关键的步骤是对因数进行拆分。在两位数乘一位数的口算中，学生发现将14拆分成10和4更容易口算。于是在两位数乘整十数的口算中，学生也尝试迁移运用以上方法，以探寻最为简便的方法。）

从未知到已知，初步实现了理解乘法算理和算法的正向迁移。

（二）笔算乘法，突破多位数乘两位数计算难点

在笔算乘法部分，将其分为两位数乘两位数（不进位）、两位数乘两位数（进位）以及多位数乘两位数三个部分。

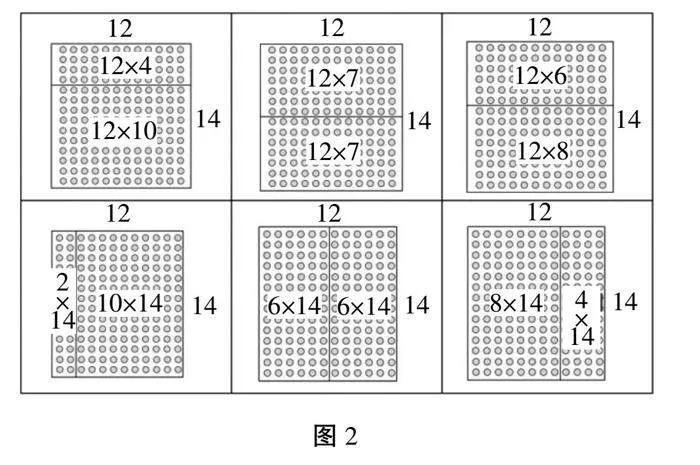
任务三：结合点子图（见图2），在点子图上圈一圈、画一画、找一找、算一算12×14，并具体说一说是怎么计算的。学生利用手中的点子图自主探究，并汇报成果。

生：我将14分成10和4，12×10利用两位数乘整十数的方法等于120，12×4等于48，120+48=168。

生：我将14分成7和7，12×7利用两位数乘一位数的方法等于84，84+84=168。

生：我将12分成10和2，14×10=140，14×2=28，140+28=168。

教师提问：这些拆分法有什么区别吗？小组比较不同的拆分方法，将其分类，并从中选出最优的方法。大多数小组认为，将14拆成10和4，或将12分成10和2计算最简便。

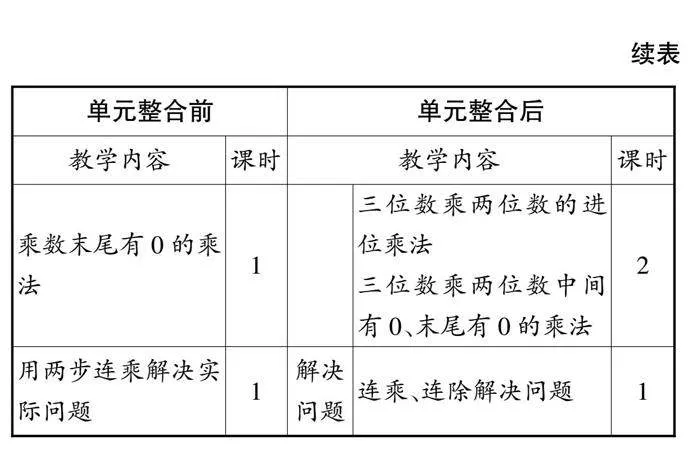
追问：我们通过分步计算得到了12×14的积。你能用一个竖式来计算12×14吗？（见图3）

在列竖式计算时，只有少数同学第二步计算是12×1=12，将2写到个位上，得到48+12=60的错误结果。对于笔算乘法，这是学生第一次构建两层楼的竖式，所有的竖式都需要经历表征、横式到竖式记录的过程。因此，针对学生的错误，笔者再次让学生在点子图上分一分，并把四次相乘得出的结果在图上圈出来，以此帮助学生理解算法和算理的关系。

追问：比较我们计算两位数乘以两位数的方法，看看它们有什么相同之处。两位数乘两位数的算理是什么？

师生讨论发现，两位数乘两位数的算理是根据数和乘法的意义，把其中一个因数拆分成不同计数单位的数之和的形式，然后再分别相乘，把积加起来。它们都是把两位数乘两位数这一新知识转化成学过的两位数乘整十数或一位数乘一位数的旧知识，其中运用到了迁移和转化的思想方法。

（设计意图：本环节引导学生通过把“两乘一加”的横式推算过程在竖式中表示出来，自主完成由横式推算走向竖式算法建构的过程。）

任务四：列竖式计算43×65，并说明笔算过程及竖式中每一步的含义。（答案见图4）

（设计意图：43×65的计算涉及两位数乘以两位数进位的运算规律。这一环节让学生迁移前面所学的规律自己列竖式计算，并说明笔算过程及竖式中每一个数字的含义。这样既帮助学生进一步掌握竖式计算的顺序和方法，又加深学生对竖式含义的理解，从而达到真正理解两位数乘两位数笔算乘法的算理，巩固算法。）

（三）迁移探究，多位数乘两位数计算方法

三位数乘两位数的算理、算法与多位数乘一位数、两位数乘两位数是一致的，只不过三位数乘两位数多了一个计算步骤。在教学过程中，笔者放手让学生进行自主探究，将已有的乘法竖式方法迁移到当前的学习中，以促进学生迁移能力的提升。两位数乘两位数和三位数乘两位数，都是先用第一个因数去乘第二个因数的个位，得到几个一，再用第一个因数去乘第二个因数的十位，得到几个十，最后把两次乘得的结果合起来。两位数乘两位数，先用两位数去乘第二个因数的个位，得数从个位写起，表示多少个一，再用两位数去乘第二个因数的十位，得数从十位写起，表示多少个十，最后再把两次的得数合起来。三位数乘两位数同样也是先用第二个因数的个位去乘两位数，得数从个位写起，表示多少个一，再用两位数去乘第二个因数的十位，得数从十位写起，表示多少个十，最后再把两次的得数合起来。通过对比可以发现，三位数乘两位数与两位数乘两位数的方法相同，都是在“先分再合”，这样自然而然地就把两位数乘两位数的计算方法迁移到三位数乘两位数中了。根据这样的规律，学生可以进一步推理出三位数乘三位数、四位数、五位数等的算理和算法，接着类推到多位数乘多位数。

五、结论

在本单元教学中，笔者利用前测结果了解学生迁移能力及对两位数乘两位数的学习起点，明确学生的学习难点在于对算理的理解；在教学中引领学生回顾乘法的意义、两位数乘一位数的算理，激活学生已有知识和经验。在这个基础上，笔者牢牢抓住乘法的本质，引导学生明确两位数乘两位数运算的本质就是将其中一个因数进行拆分，将其转化成一位数或整十数乘两位数来计算。笔者在类比探究的过程中，帮助学生搭建新旧知识的沟通桥梁，学会迁移运用旧知识来解决新问题，最终促进学生迁移能力的提高。

（作者单位：泗阳县实验小学）

编辑：常超波