分子动力学模拟中压强和局部压强的计算

摘 要：快速精确计算系统的压强在分子动力学模拟中是非常重要的。文章对具有势能限制和周期性边界条件的立方型模拟盒子的不同密度系统进行了分子动力学模拟。模拟结果表明压强计算存在较明显的涨落，而保持系统温度恒定等特定方法引入的随机力等将显著增大涨落，但对压强的统计平均值影响较小。将系统中多体作用的维里按作用粒子均分，在此基础上获得单粒子压强，可用于局部区域的压强计算。

关键词：分子动力学模拟；压强；局部压强；涨落

中图分类号：TQ021.2； O642.5"" 文献标识码：A"" 文章编号：1673-1794（2024）05-0001-04

作者简介：冯剑，滁州学院材料与化学工程学院教授，博士，研究方向：分子模拟（安徽 滁州 239000）。

1 前言

压强（或压力）是描述系统（或体系）性质的一个重要物理量，系统的状态和其他性质一般会随压强变化而发生变化。在分子动力学模拟中，精确计算系统的压强在流体性质研究、相平衡计算等多种场合有着广泛的应用。

分子动力学中计算压强的表达式主要通过维里定理^[1]获得，也可以定义一个形状参数^[2]或者从广义能量均分定理并结合经典力学的维里定理导出^[3]。尽管通过这些方法获得的是容器限制系统的压强计算式，但这个表达式也可以稍加变化而适用于周期性边界条件系统^[2]。该压强计算式还可以利用统计力学的径向分布函数理论导出^[4]。通过这些方法获得的压强计算式由两项组成，一项是忽略粒子间相互作用的理想气体贡献，该项与系统的温度有关，它反映了粒子动量流施加的压强。另一项是考虑粒子间相互作用的贡献项，它可以看作是偏离理想气体的校正项，它的贡献来自一个称之为维里的物理量。在分子动力学模拟中计算的压强一般都有较大的涨落，如使用Berendsen恒温恒压方法，进行300K、1atm的模拟，其压强涨落达到几百个大气压^[5]。分子动力学模拟中通常采用维里公式计算压强，一些学者尝试采用其他方法来计算系统的压强，如de Miguel等^[6]使用体积微扰来计算系统的压强。对于刚性分子体系，Glaser等^[7]通过统计力学导出了一种压强计算方法，修正了早期文献中的错误。

对于非均匀系统，如多相平衡系统以及稳态流动等非平衡系统则需要能正确计算出局部区域的压强。Heinz等^[8]在解决多体局部压强的计算时，将空间划分为微小局部区域，根据区域再将多体划分为二体来计算。Lion等^[9]则将多体按其在局部区域的分布情况，划分为两体作用，维里在两体作用距离上均匀分配，进而获得局部压强。这些方法需要先给出系统的局部区域形状再考虑多体与局部区域的交叠情况进行计算，不具有通用性。很多软件没有提供局部压强计算的方法，需要研究者获取模拟过程中产生的粒子速度、力和位移等数据自行根据研究对象编程解决。

2 计算方法

2.1 系统压强

对于一个具有N个粒子的系统，获得压强计算的统计公式且具有启发意义的推导是从以下的形状量I开始^[3]：

I=12∑Ni=1miri·ri（1）

其中mi是i粒子的质量，ri是i粒子的位移。对于刚体来说，该量就是转动惯量的一半。将该量对时间t求导两次，并利用牛顿第二运动定律，得：

d2Idt2=∑Ni=1miv2i+∑Ni=1Fi·ri（2）

式中vi为i粒子的瞬时速度，Fi为i粒子受到的瞬时作用力。右侧第一项为系统动能的2倍，第二项为系统的维里。考虑该N个粒子系统被外场或容器限制在一定的体积内。右侧的力Fi进一步划分为内部粒子间的作用F^int和壁面及外场对粒子的作用F^ext（并非每个内部粒子都受到外力作用，没有则值为0）。对上式进行时间平均（使用SymbolaC@SymbolqC@表示），在无穷长的统计时间下，由于粒子的位置和速度是有限的，（2）式的统计值等于0^[1，3]，则

〈∑Ni=1miv2i〉+〈∑Ni=1F^inti·ri〉+〈∑Ni=1F^exti·ri〉=0（3）

移项，得

〈∑Ni=1miv2i〉+〈∑Ni=1F^inti·ri〉=〈∑Ni=1－F^exti·ri〉（4）

外力用作用于壁面的平均压强p乘以容器壁面面积代替，再利用高斯定理^[1]可获得（4）式右侧值为3pV，V是系统的体积。如果考虑容器为方形这一特殊模拟盒子，坐标原点在盒子中心，盒子边长为Lx、Ly和Lz，则盒子边缘的坐标为±Lα/2，αSymbolNC@（x，y，z）。在α方向，垂直该方向的盒子表面积为Aα，压强为p，其作用力为pAα。据此，同样可以得出相同结果。

〈∑Ni=1－F^exti·ri〉=∑α∈（x，y，z）pAαLα=3pV（5）

由此，可以获得容器中的压强计算式为

p=13V〈∑Ni=1miv2i〉+〈∑Ni=1F^inti·ri〉（6）

它完全通过容器内部粒子的相互作用来计算。利用（3）式，同样可以通过统计容器壁面对容器内粒子施加的外力来计算系统的压强，即

p=13V〈∑Ni=1－F^exti·ri〉（7）

将（6）式获得的压强记为p^int，（7）式获得的压力记为p^ext，则（3）式反映了这两种方式计算的压强差值，即

Δp=13V〈d2Idt2〉=p^int－p^ext（8）

前面推导的公式是容器限制系统中的压强计算式。可以证明^[3，4]，（6）式适用于具有周期性边界条件的系统。其中内力的计算时须考虑粒子间及粒子与映像粒子间的最短距离。

对于周期性模拟盒子，处于边界粒子受到的外力来自中心模拟盒子中其他粒子的映像。将上面的形状量定义用于该系统，同样可得

Δp=13V（〈∑Ni=1miv2i〉+〈∑Ni=1F^inti·ri〉+〈∑Ni=1F^exti·ri〉）（9）

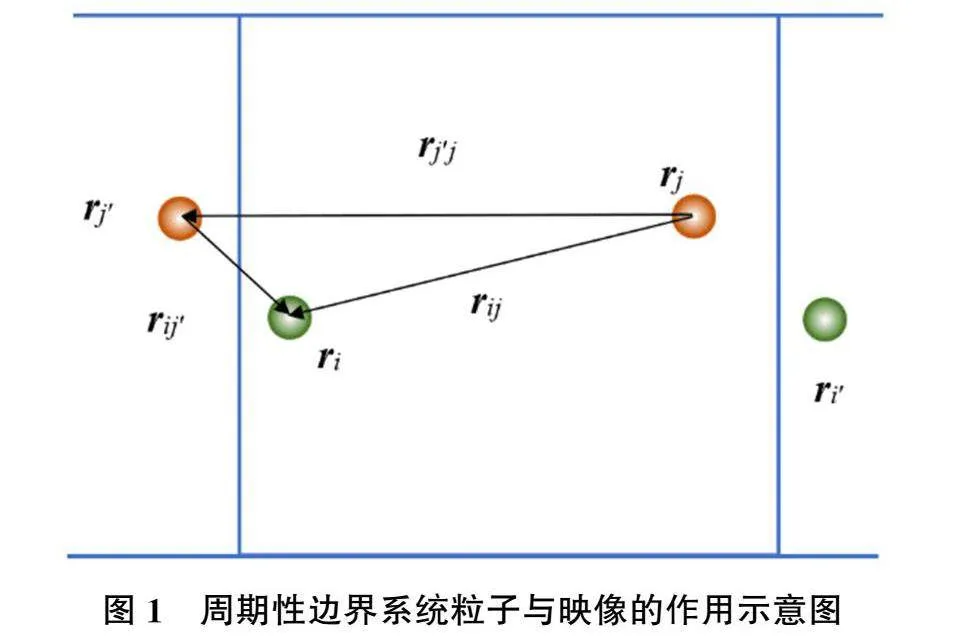
图1是具有周期性边界的二维模拟盒子示意图。其中i、j粒子是中心模拟盒子中的两个发生相互作用的粒子。它们分别与相应粒子的映像j′和i′作用，其中用撇号表示某粒子的映像。对于中心盒子，这种作用属于外力。则这两个粒子的维里为

F^extij′·ri+F^extji′·rj=F^extij′·（ri－rj）=F^extij′·（ri－rj′+rj′－rj）=F^extij′·rij′+F^extij′·rj′j（10）

其中rij=ri-rj，其他项以此类推。如果粒子间的力为两体作用，则（9）式可变形为：

Δp=13V〈∑Ni=1miv2i〉+〈∑Ni=1∑i－1j=1Fij·rij〉+13V〈∑iFij′·rj′j〉（11）

其中

rj′j=lLx+mLy+nLz（12）

从图1可以看出，（11）式中l、m和n取值根据rij值大小和符号取1、0或-1。（11）式右侧括号中的项为通过系统内部作用计算的压强p^int。其中rij是考虑粒子间以及粒子和映像间的最短距离，即处在边界附近的i粒子和j粒子将和映像作用，其取值实际为r′ij，见图（1）。右侧最后一项是一个粒子与另一个粒子映像的作用力与另一个粒子和其映像矢量的点乘，该项对应的压强记为p^ext。对于具有周期性边界条件的系统，对中心盒子中的粒子施加外力的映像粒子位置不是固定的，仅使用该力计算的压强没有考虑这些映像粒子运动对压强的贡献。

2.2 局部压强

如果图（1）中的中心区域并非整个模拟盒子，而是模拟盒子中的一个区域，则这个区域之外的粒子将不再是该区域粒子的映像。对于这样的局部区域的压强计算就需要考虑跨越区域的二体或多体作用产生的维里如何在这些区域中分配^[8，9]。如对于一个二体作用，它的维里为：

wij=Fi·ri+Fj·rj=Fic·ric+Fjc·rjc=Fij·rij（13）

其中第二个等式中的c为rij上的任意参考点。将参考点设为j，则得出第三个等式，该式也是前面计算二体作用的维里式。一个合理的想法是，将c点设置在rij与局部区域的边界处，这样第二个等式中的二项分别是该二体对的维里在这两个区域中的分配。如果i粒子和j粒子均落在计算区域之外但与该区域有2个交点，则按这两个点间的距离与总作用距离占比分配^[9]。如果是三体作用，如键角作用，将区域内外的2个粒子看作一个粒子，再与另外1个粒子形成二体^[9]。通过计算这个三体围成的三角形与计算区域的重叠的面积来计算维里的分配也不失为一个方法。由此可见，对于多体作用按照这样的方法分配维里是非常复杂的，也无法给出通用程序，必须具体问题具体对待。

压强由粒子与真实或虚拟壁面的相互作用产生，因而系统的压强也是每个粒子作用的表现。对于二体和多体问题，一个合理的考虑是系统压强在每个粒子上的分配。通过（6）式可以看出，主要需解决维里在粒子上的分配问题。遗憾的是，对于二体或多体作用，无法找到唯一的净作用力为0的力心，如二体连线上任意点的净作用力都为0。考虑到流体粒子总是在不停的运动，因而不同时刻（13）式中的c点处在不同位置。处于边界两侧的两个粒子，距边界的距离在不停地变化。在长时间平均下，二个粒子距离边界的平均距离应相差很小，一个可行的做法是将c点取在两个粒子连线的中点，使得两个粒子均分该作用对的维里。对于三体及以上作用对，也可以类似处理，即先计算作用对维里，然后将维里均匀分配给该作用对中的每个粒子。再将这些单个粒子维里作为粒子的性质存储，在需要计算某个区域的压强时只需要取出该区域内每个粒子的速度和维里即可计算。

2.3 模拟方法

文章中的模拟采用NVT系综，其恒温方法是Langevin方法。该方法的粒子运动方程为：

mii=Fi－γmi i+Ri（t）（14）

上式右侧是i粒子质量与其加速度的乘积。右侧为i粒子受到的总作用力，其中第一项为粒子受到的物理作用力，第二项为与速度有关的摩擦力，其中SymbolgA@为摩擦系数，第三项为随机力。后两项的引入是使得系统维持在指定温度。由于压强的贡献来自粒子的速度和受力，为了进一步降低压强的统计误差，对于没有整体运动和外场的系统，在计算时需要使系统的总动量和净作用力为0。模拟采用粗粒化模型，粒子间的作用势能为Lennard-Jones（LJ）势能，见式（15），其中εij是粒子i和粒子j的能量参数，SymbolsA@ij是两个粒子间的距离参数。（14）式中的Fi来自LJ势能的梯度负值。单位是约化的，即粒子的质量m、长度单位SymbolsA@、能量单位ε和时间单位SymboltA@等均设为1，因此文中出现的所有物理量都是没有单位的无因次量。

V（rij）=4εijσijrij¹²－σijrij6（15）

3 结果与讨论

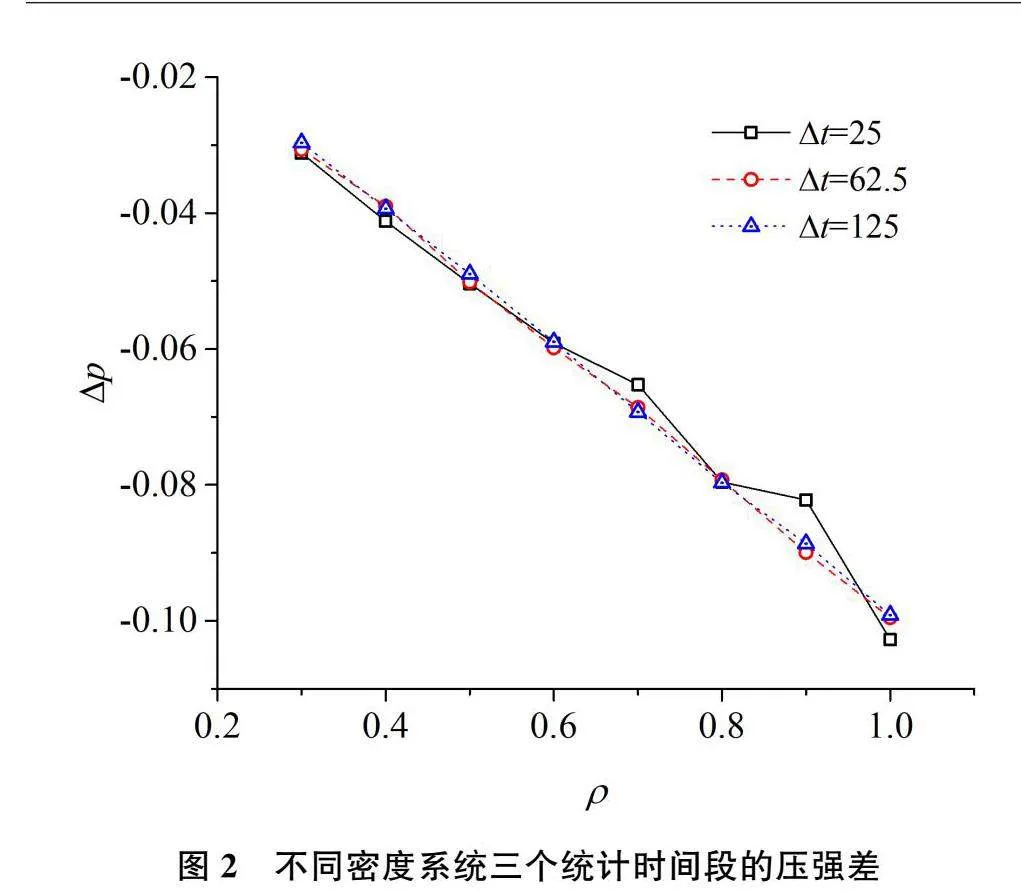
对边长为11的立方型盒子，盒子边缘具有12-6的LJ势能，它将模拟盒子中的粒子限制在盒子中运动。粒子间以及粒子与盒子壁面的LJ作用能参数为1，截断距离为2.5。将盒子与粒子作用势能为0处看作粒子可自由运动的自由空间边界，因此，自由空间的边长为10，体积为1000。分别向模拟盒子中插入300、400至1000个粒子，即彼此粒子数差100的八个系统。其数密度（简记为密度）分别为0.3、0.4、0.5、0.6、0.7、0.8、0.9、1.0。模拟的时间步长为0.00125。分别每20000、50000和100000步，即SymbolDA@t=25、62.5和125下统计系统的压强和压强差。图2就是压强差与系统密度的变化关系。由图2可以看出，按（8）式计算的压强差结果并不为0，而是接近于0的较小数值。统计时间越长，其结果越接近于0，但变化并不显著。也就是说，很难通过使用更长的统计时间来让这些系统的压强差接近于0。由该图可以看出，系统的粒子数越多，密度越大，压强差偏离0越远，这可能是误差累积的结果。压强差的负号反映了由系统内部粒子作用计算的压强略小于由容器壁面产生的外力计算的压强。

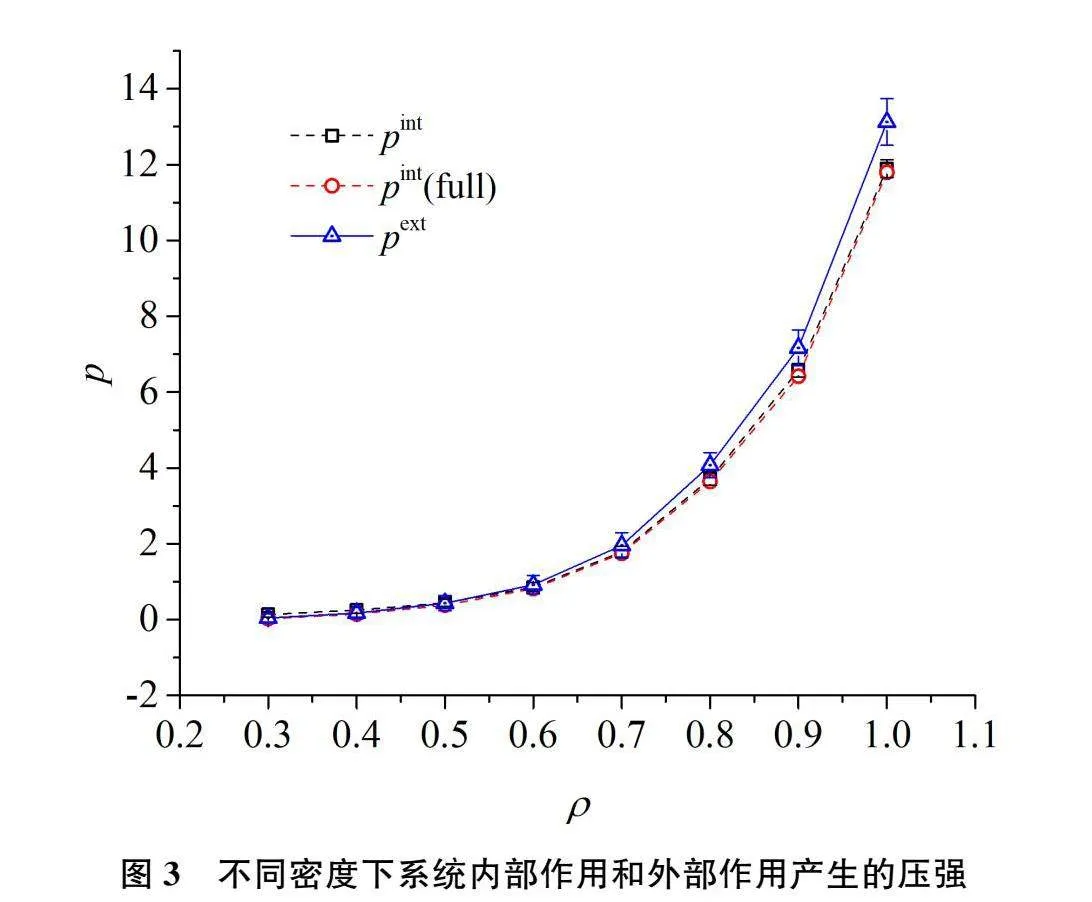
图3是统计时间间隔SymbolDA@t=62.5时，由系统内部作用统计的压强和外部作用统计压强随系统数密度的变化关系。其中p^int未包含Langevin恒温法中摩擦力和随机力的维里对压强的贡献，而p^int（full）则包括了这两个力的维里贡献。图中p^int和p^int（full）几乎重合表明，摩擦力和随机力的考虑与否对系统的压强平均值影响较小。但p^int（full）的涨落比p^int大得多。由于p^int（full）的偏差太大，图3中给出了p^int和p^int（full）数据的误差范围，而无法给出p^int（full）的误差范围。p^int的相对偏差在2%～50%之间，如ρ=0.3时压强为0.03751±0.01784；ρ=1.0时压强为11.8929±0.23753。而p^int（full）的相对偏差则大得多，如ρ=0.3时压强为0.025968±11.767；ρ=1.0时压强为11.794±25.691，其偏差约是平均值的453倍和2倍。出现这种情况的原因是这两种力均是单体力，在较小空间其净作用力不为0；尤其是随机力，它不是一个关于位置的连续函数，对压强涨落的影响尤为显著。系统密度越小，压强的相对偏差越大。由此可见，不考虑摩擦力和随机力对维里的贡献，统计的压强值相对偏差较小，考虑它们的贡献则偏差达到几倍至几百倍。也就是说，在使用Langevin恒温方法时，计算系统压强可以不考虑摩擦力和随机力对维里的贡献。图3也显示了系统内部作用统计的压强略小于通过外力统计的压强。其差异比图2略大是因为指定粒子自由运动的自由空间边长为10，这没能准确反映由软粒子组成模拟盒子与系统粒子发生作用的实际边界。

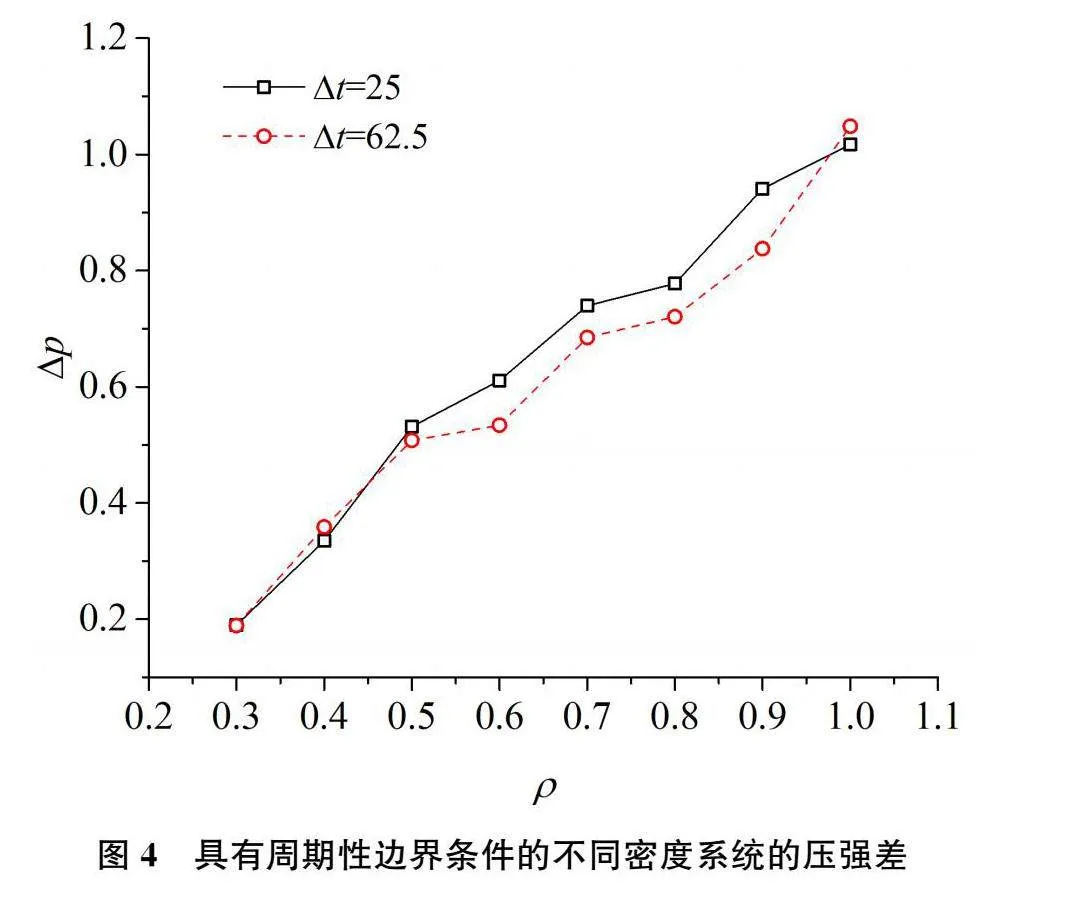
对于三个方向均具有周期性边界的三维立方体模拟盒子，同样模拟了数密度从0.3、0.4、0.5、0.6、0.7、0.8、0.9、1.0的八个系统，其中立方型盒子边长为10。图4给出了两个统计时间间隔，按（11）式计算的压强差。可以看出，周期性边界条件的系统，压强差与0的偏离值明显大于具有壁面限制的系统。延长统计时间虽能减小偏离值，但与0的偏离依然较大。从正的数值可以得出按系统内部作用计算的压强大于将映像作用看作外力的压强。究其原因，可能在于虽将与模拟盒子边缘粒子的映像作用看作外力，但不同于前述的固定边界，该粒子是运动的，动量对压强有贡献，而按（11）式右侧最后一项计算的压强忽略了动量贡献。对于密度ρ=0.3的系统，SymbolDA@p=0.19，按理想气体方程pV=NkT计算，需考虑模拟盒子外部190个映像粒子的动量贡献就可以将压强差变为0。对于ρ=1.0，则该粒子数在1000个左右。

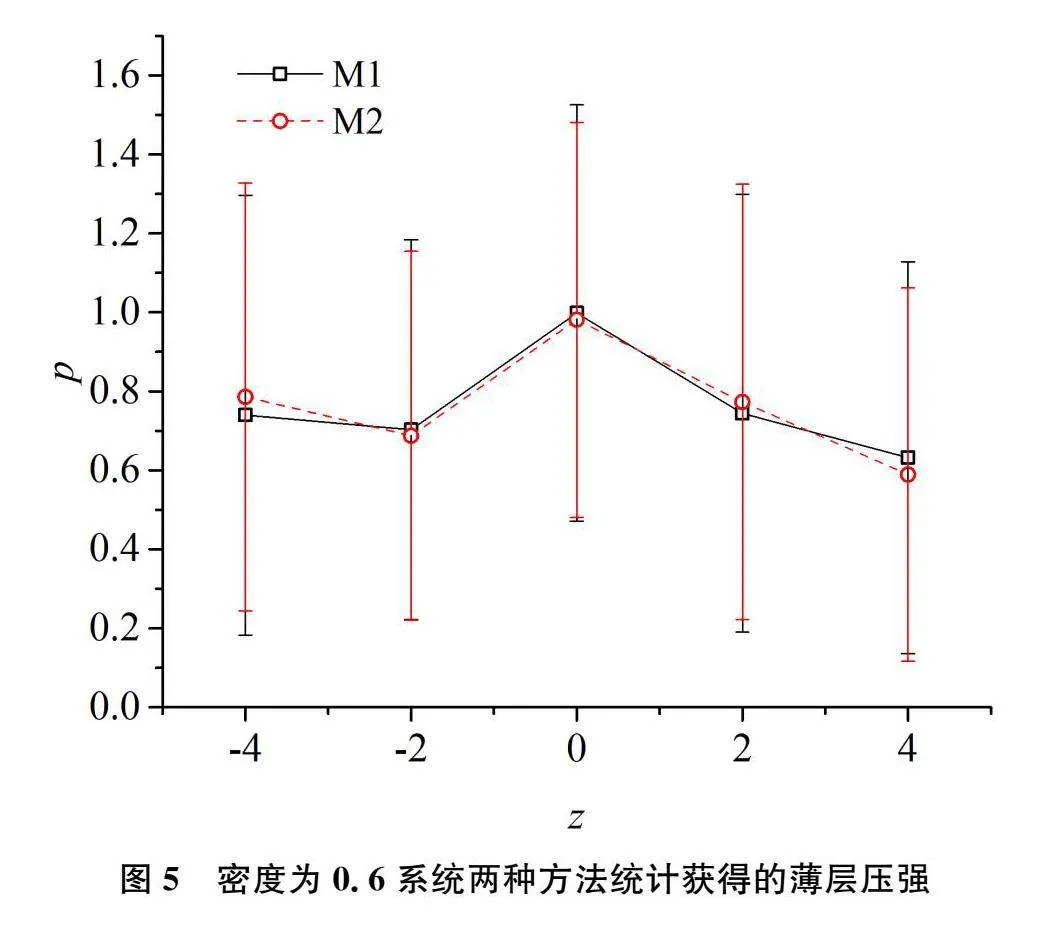
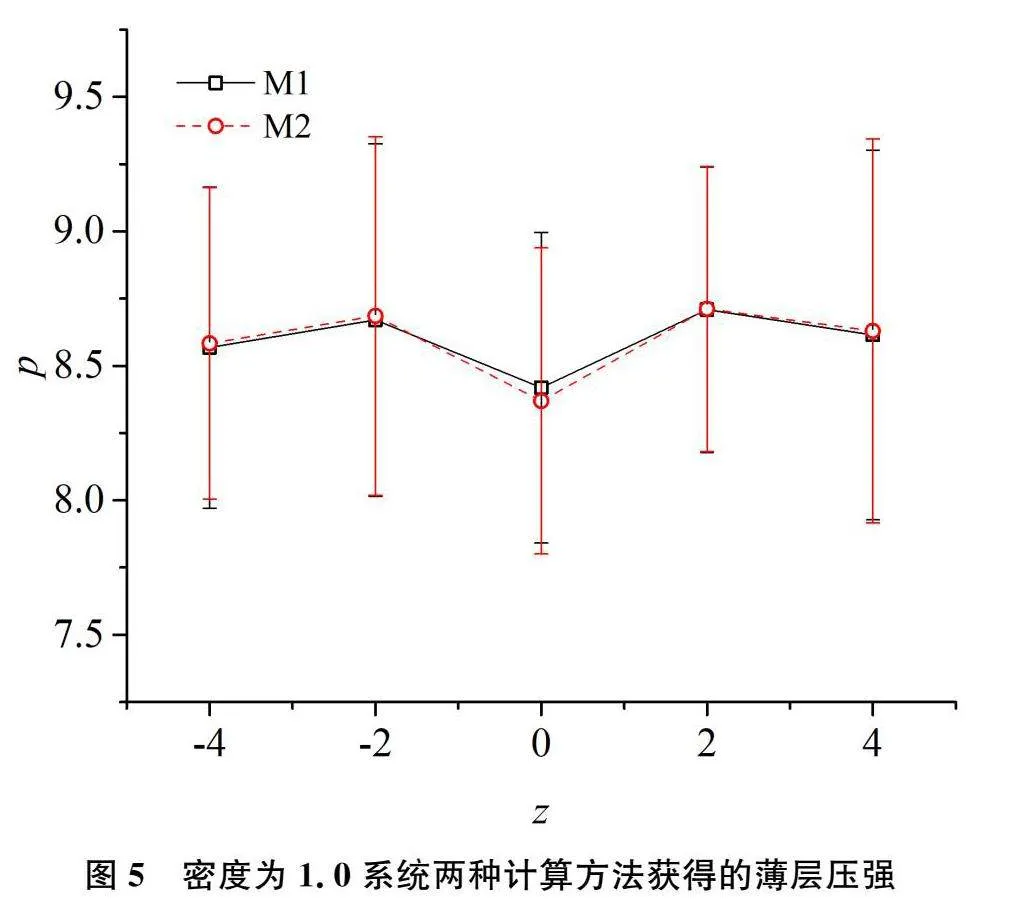
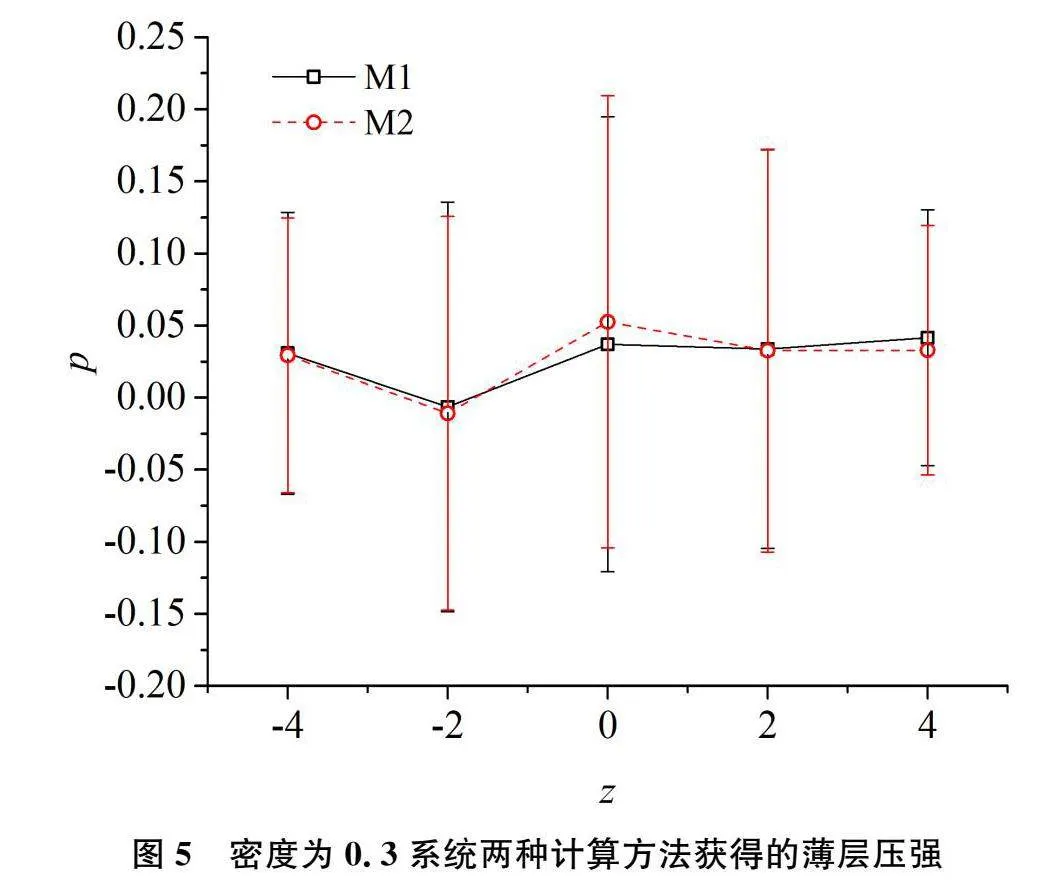
将该边长为10的模拟盒子沿z方向均匀划分为5个薄层，其中每层厚度为2。采取前述的两种局部压强统计方法统计这5个薄层的压强。第一种是将维里按作用距离分配^[9]。系统内粒子相互作用的截断距离为2.5，薄层厚度为2。按该方法，有一些作用粒子对的2个粒子尽管均未落入同一薄层，也会对该层有较大贡献。该方法记为M1。本研究将压强分配到每个粒子的方法记为M2。对于密度从0.3到1.0的八个系统进行模拟比较，两种统计方法给出的结果是一致的。图4和图5分别给出了ρ=0.3和ρ=1.0的系统由这两种压强统计方法获得结果的比较。由这两个图可以看出，两种统计方法获得的结果接近，统计值差异均在统计误差范围内。

为了进一步验证作用粒子对的质量差异是否影响压强的按粒子均分方法，模拟了两种粒子等密度混合，其总密度从0.3至1.0的八个系统。即对于总密度为0.3的系统，其中每种粒子密度为0.15。两种粒子的质量分别为1和10。为了更好地考察方法的差异，LJ作用势的能量参数选择为ε11=ε22=2，ε12=1，让同种粒子有更强的自聚性。距离参数SymbolsA@ij均为1。系统的温度为2。模拟结果表明两种方法统计的压强值是一致的。图6给出了ρ=0.6下两种方法获得的薄层压强。由该图可以看出，每个薄层两种方法计算的压强接近，其差异均在压强的统计误差范围之内。也就是说，两种粒子尽管质量相差10倍，但均分维里同样是有效的。由（15）式可以看出，粒子相互作用的LJ势能仅是能量和距离的函数，与粒子的质量无关，更大质量的粒子并不会分得更多的维里。

4 结论

当前分子动力学模拟中的压强计算主要由系统中粒子运动的动能和相互作用产生的维里获得。由于粒子的速度和维里存在一定的分布，压强的计算值必然存在一定的涨落。但更显著的涨落常常是对运动方程改造而引入的额外作用所致，如Langevin恒温方法中的随机力和摩擦力。在系统压强计算中忽略随机力等的维里对压强的贡献，不仅不会带来明显的误差，还有助于获得更加稳定的平均值，从而也能获得稳定的其他性质。对于多体作用的系统，将多体作用的维里按多体粒子数均分，再将各类作用中每个粒子所分配得到的维里累积，连同其动能可获得单粒子压强，该压强可方便地用于任意区域压强计算而不会产生明显的差异。

［参 考 文 献］

［1］ GOLDSTEIN H，POOLE C，SAFKO J.Classical mechanics（3rd edition）[M].北京：高等教育出版社，2005：83-86.

[2] PATHRIA R K，BEALE P D.Statistical Mechanics[M].4th edition.Oxford：Academic press，2022：62-65.

[3] HAILE J M. Molecular dynamics simulation.Elementary methods[M].New York：Wiley，1992：332-339.

[4] TUCHERMAN M E.Statistical mechanics：Theory and molecular simulation[M].Oxford：Oxford university press，2010：160-166.

[5] FIELD M J.A practical introduction to the simulation of molecular systems （2nd edition）[M].北京：世界图书出版社，2014：245-246.

[6] DE MIGUEL E，JACKSON G.The nature of the calculation of the pressure in molecular simulations of continuous models from volume perturbations[J].J Chem Phys，2006，125：164109.

[7] GLASERA J，ZHA X，ANDERSON J A，et al.Pressure in rigid body molecular dynamics[J].Computational Materials Science，2020，173：109430.

[8] HEINZ H，PAUL W，BINDER K.Calculation of local pressure tensors in systems with many-body interactions[J].Phys. Rev. E， 2005，72：066704.

[9] LION T W，ALLEN R J.Computing the local pressure in molecular dynamics simulations[J].J Phys： Condens Matter，2012，24：284133.

Pressure and Local Pressure Calculations in Molecular Dynamics Simulations

Feng Jian

Abstract： Rapid and accurate calculation of the pressure of the system are very important in molecular dynamics simulations. In this paper， molecular dynamics simulations are performed on a different-density system of cubic simulation boxes with potential energy confinement and periodic boundary conditions. The simulation results show that there is a significant fluctuation in the pressure calculation， while the random force introduced by specific methods such as keeping the system temperature constant will significantly increase the fluctuation， but have little influence on the statistical average of pressure. The Virial of the many-body interaction in the system is divided equally according to the acting particles， and the single-particle pressure is obtained on this basis， which can be used for the calculation of the pressure in the local region.

Key words：molecular dynamics simulation; pressure; local pressure; fluctuation

责任编辑：陈星宇