例谈空间几何体的“降维”方法

【摘要】空间几何体是高中数学立体几何板块的重要研究对象，是空间中点、线、面位置关系的主要载体．空间几何体的“降维”分析，即将空间立体几何问题转化为平面几何问题，是研究立体几何的一般方法，亦可培养学生的化归转化能力和直观想象素养．

【关键词】空间几何体;“降维”分析;化归转化;直观想象

高中数学的立体几何问题，尤其是与几何体有关的问题，常常需要转化为平面图形进行分析，本文称之为“降维”．几何体中常见的夹角问题、截面形状问题、距离问题、位置关系问题以及动点的轨迹问题，大都可以通过适当转化得以简化．本文主要提出三种“降维”分析的角度，以供读者参考、讨论、补充．

1“降维”方式1：展开

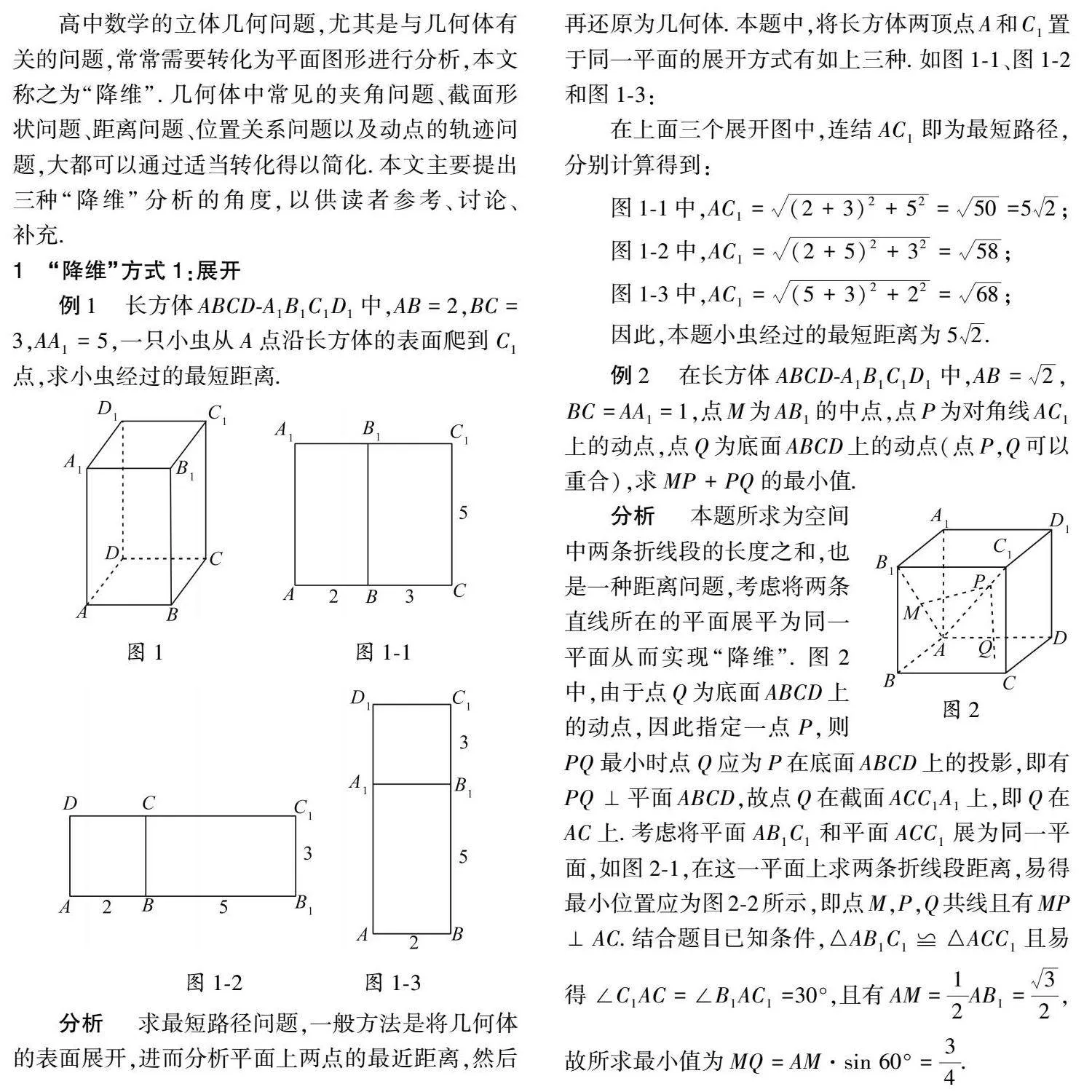
例1长方体ABCD-A1B1C1D1中，AB=2，BC=3，AA1=5，一只小虫从A点沿长方体的表面爬到C1点，求小虫经过的最短距离．

分析求最短路径问题，一般方法是将几何体的表面展开，进而分析平面上两点的最近距离，然后再还原为几何体．本题中，将长方体两顶点A和C1置于同一平面的展开方式有如上三种．如图1-1、图1-2和图1-3：

在上面三个展开图中，连结AC1即为最短路径，分别计算得到：

图1-1中，AC1=（2+3）2+52=50=52；

图1-2中，AC1=（2+5）2+32=58；

图1-3中，AC1=（5+3）2+22=68；因此，本题小虫经过的最短距离为52．

例2在长方体ABCD-A1B1C1D1中，AB=2，BC=AA1=1，点M为AB1的中点，点P为对角线AC1上的动点，点Q为底面ABCD上的动点（点P，Q可以重合），求MP+PQ的最小值.

图2分析本题所求为空间中两条折线段的长度之和，也是一种距离问题，考虑将两条直线所在的平面展平为同一平面从而实现“降维”．图2中，由于点Q为底面ABCD上的动点，因此指定一点P，则PQ最小时点Q应为P在底面ABCD上的投影，即有PQ⊥平面ABCD，故点Q在截面ACC1A1上，即Q在AC上．考虑将平面AB1C1和平面ACC1展为同一平面，如图2-1，在这一平面上求两条折线段距离，易得最小位置应为图2-2所示，即点M，P，Q共线且有MP⊥AC．结合题目已知条件，△AB1C1≌△ACC1且易得∠C1AC=∠B1AC1=30°，且有AM=12AB1=32，故所求最小值为MQ=AM·sin 60°=34．

展开图是将空间几何问题平面化最为直接的方法之一，通过这样的方式，我们可以将立体几何问题转化为平面几何问题，借助平面几何有关定理即可得解．

2“降维”方式2：截面

图3例3如图3，正方体ABCD-A1B1C1D1的棱长为23，动点P在对角线BD1上，过点P作垂直于BD1的平面α，记这样得到的截面多边形（含三角形）的周长为y，设BP=x，则当x∈［1，5］时，求函数y=f（x）的值域．

分析本题涉及到正方体中垂直体对角线的截面问题．图3中所示三角形应为平行于平面AB1C的等边三角形，因此随着x增大，三角形周长也在不断增大，直至△AB1C处．x继续增大，截面开始出现六边形，如图3-1，此时六边形的六条边可以看成三对，每一对即为图中的MN和NQ.实际上，MN+NQ的值始终等于AB1，可参考图3-2理解，也就是说，截面虽然变为六边形，其周长并没有改变，直至截面再次转为△A1DC1，而后周长逐渐变小．因此不难得出，当x∈［1，5］时，函数y=f（x）的值域为［36，66］．

例4正方体ABCD-A1B1C1D1的棱长为1，点P，Q，R分别是棱A1A，A1B1，A1D1的中点，以△PQR为底面作正三棱柱，若此三棱柱另一底面三个顶点也都在该正方体的表面上，求这个正三棱柱的高.

图4分析例题3的设问直接指向了几何体的截面问题，我们只需要对截面的特征熟练掌握即可，而本题的问题需要我们转化为截面问题．如图4，根据前面的分析，我们很容易判断出平面PQR平行于平面AB1D1，因此三棱柱另一底面必然也与平面AB1D1平行．此外，在正方体中，还有A1C⊥平面AB1D1，因此正三棱柱的三条侧棱都与A1C平行，取其中一条研究，不难将问题转化为：过图4中的P点，求作直线A1C的平行线，故问题只需要在点P和直线A1C所在的平面上研究.进一步地，在△A1AC中，取AC中点T，则必有PT∥A1C，因此正三棱柱的高即为PT=12A1C=32．

在例题3和例题4中，分别用到了几何体的截面图，相对于展开图，截面图更多的用于定性分析之后的“降维”操作，也就是说，我们已经对题中的线线关系或线面关系有了具体的认识，而后根据其所在的截面进行进一步分析．

实际上，几何体的截面问题是非常好的空间想象能力训练的素材，以正方体为例，其特殊截面如图4-1所示，可以根据具体问题再行补充．

3“降维”方式3：投影

新教材[1]中弱化了对几何体三视图的要求，但在很多情境中，将几何体或某条直线投影到特定平面之后分析仍然会对计算有所简化．

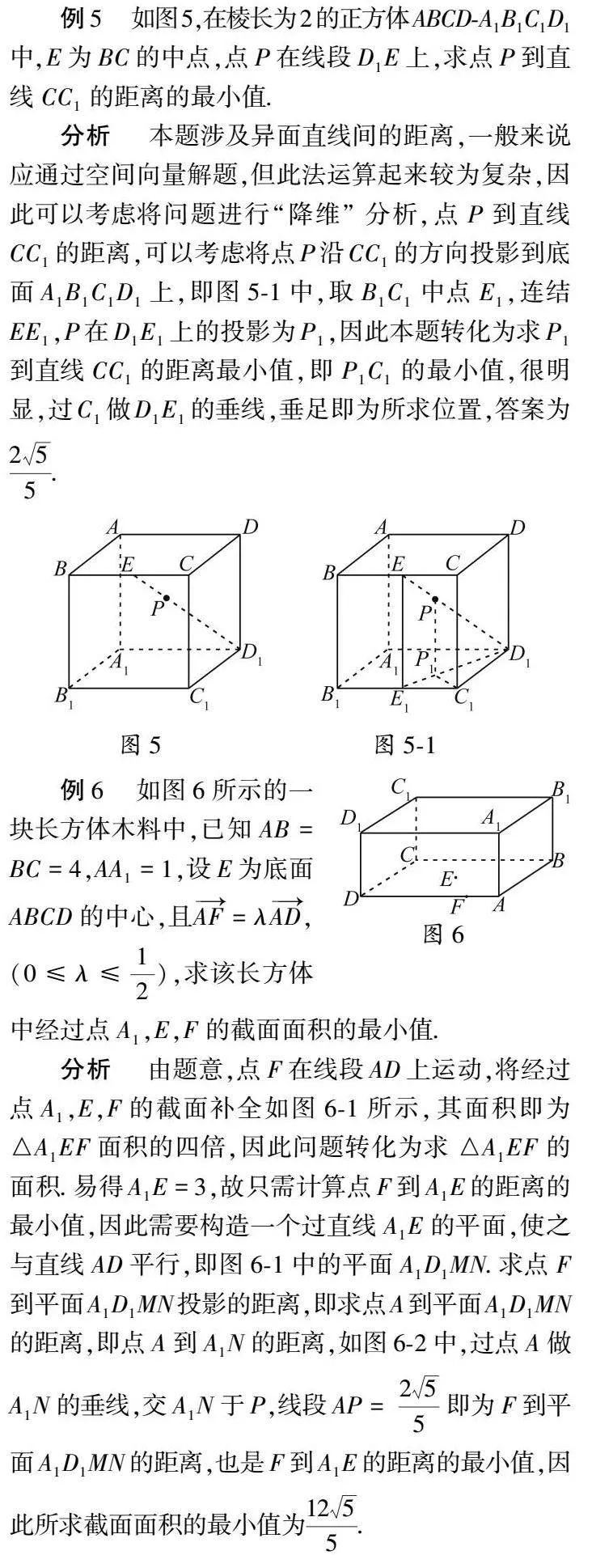
例5如图5，在棱长为2的正方体ABCD-A1B1C1D1中，E为BC的中点，点P在线段D1E上，求点P到直线CC1的距离的最小值．

分析本题涉及异面直线间的距离，一般来说应通过空间向量解题，但此法运算起来较为复杂，因此可以考虑将问题进行“降维”分析，点P到直线CC1的距离，可以考虑将点P沿CC1的方向投影到底面A1B1C1D1上，即图5-1中，取B1C1中点E1，连结EE1，P在D1E1上的投影为P1，因此本题转化为求P1到直线CC1的距离最小值，即P1C1的最小值，很明显，过C1做D1E1的垂线，垂足即为所求位置，答案为255．

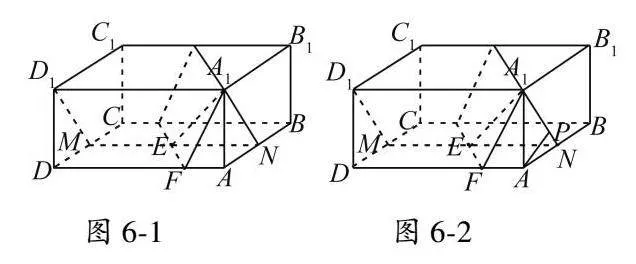
例6如图6所示的一块长方体木料中图6，已知AB=BC=4，AA1=1，设E为底面ABCD的中心，且AF=λAD，（0≤λ≤12），求该长方体中经过点A1，E，F的截面面积的最小值．

分析由题意，点F在线段AD上运动，将经过点A1，E，F的截面补全如图6-1所示，其面积即为△A1EF面积的四倍，因此问题转化为求△A1EF的面积．易得A1E=3，故只需计算点F到A1E的距离的最小值，因此需要构造一个过直线A1E的平面，使之与直线AD平行，即图6-1中的平面A1D1MN．求点F到平面A1D1MN投影的距离，即求点A到平面A1D1MN的距离，即点A到A1N的距离，如图6-2中，过点A做A1N的垂线，交A1N于P，线段AP=255即为F到平面A1D1MN的距离，也是F到A1E的距离的最小值，因此所求截面面积的最小值为1255．

这里所提到的投影，实际上是通过对题意的转化，将题中所求的距离问题转化为其他特殊点到投影面的距离，进而转化为点到直线的距离．在涉及其他空间位置关系时，也可以通过将几何体投影到指定平面进行分析，例如研究异面直线夹角问题，运用三垂线定理解决线面关系等等，这些问题都比较熟悉，此处不再展开．

以上的三种“降维”方法是分析空间几何体中位置关系和数量关系的常用方法，“立体问题平面化”是我们分析复杂几何体问题的首要思考方向，通过展开图、截面图和适当的投影可以将问题进行转化或简化；“平面问题三角化”实际上是转化后的继续分析，例如平面几何中的正、余弦定理，平面向量甚至是解析几何，都可以恰当的融入其中，这在本文中的几道例题中均有充分的体现．

当然，解决立体几何问题的方法还有很多，例如平移、延展、截割、补形、构造辅助几何体以及运用空间向量等等，无论是哪种方法，其根本抓手都是空间几何体的基本性质以及空间点线面的基本结论，只有熟知这些基本内容，掌握研究立体几何的基本方法，才能不断生发出新的解决问题思路，从而恰当的运用化归转化思想使问题得以简化，进而不断运用平面几何中的素材强化空间几何问题的直观想象素养[2]．

参考文献

[1]人民教育出版社，课程教材研究所，中学数学课程教材研究开发中心. 普通高中课程标准实验教科书·数学：B版[M]. 北京： 人民教育出版社，2020.

[2]章建跃. 树立课程意识，落实核心素养[J]. 数学通报，2016，55（05）：1-4.

作者简介

崔鹏（1984—），男，北京人，中学高级教师、年级组长、北京数学会会员、北京市骨干教师、海淀区学科带头人；研究方向为数学课堂教学、教材教法分析以及数学学科德育理论研究与课堂实践.

基金项目

北京市海淀区教育科学“十四五”规划课题“深度学习视域下的数学教学情境建构与应用”（HDGH20230373）.