基于GGB对极点极线背景下圆锥曲线问题的探究与推广

【摘要】极点极线背景下的圆锥曲线问题是高考数学的高频考点，GGB是一款能够同时处理几何与代数问题的功能强大的动态数学软件.对近五年来极点极线背景下的圆锥曲线高考题进行梳理，并借助GGB软件对极点极线背景下的定点问题、定直线问题、平行垂直问题和倾斜角与斜率问题进行了探究与推广.

【关键词】极点极线；圆锥曲线；GGB；信息技术

1引言

GeoGebra软件（以下简称GGB）是由美国佛罗里达州亚特兰大学的数学教授Markus Hohenwarter设计的一个动态数学软件，只需点击或者输入命令就可以实现画图、作切线极线等功能，给解析几何的研究带来了极大的便利.

极点极线背景下的圆锥曲线问题一直是高考考查的重点与难点，选取近年来极点极线背景下的高考圆锥曲线大题，分析其背景，并借助GGB对其进行探究与推广，以期为教学、命题、解题带来一定的参考与启示.

2极点极线的相关概念

2.1极点极线的定义

代数定义：二次曲线C：Ax2+By2+Cxy+Dx+Ey+F=0（A2+B2≠0），点P（x0，y0）与直线Ax0x+By0y+Cx0y+y0x2+Dx0+x2+Ey0+y2+F=0是二次曲线C的一对极点与极线.

几何定义：以椭圆为例如图1，点P不在圆锥曲线上，过点P作圆锥曲线的两条割线，分别交曲线于A，B，C，D四点，弦AC与BD的交点为M，直线AD与BC的交点为N，则直线MN为点P的极线，直线PN为点M的极线，直线PM为点N的极线.△PMN称为自极三角形，其中每一顶点与其对边所在的直线为一组极点极线[1].

2.2调和点列与调和线束

调和点列：对于线段AB的内分点C和外分点D，若满足CACB=DADB，则称点列A，C，B，D是调和点列，点列D，B，C，A也是调和点列.以椭圆为例，如图2，过点Q作直线与圆锥曲线交于A，B两点，与点Q的极线交于点P，则A，Q，B，P是调和点列.

调和线束：如图3，若A，C，B，D是调和点列，O为直线外任意一点，则直线OA，OC，OB，OD为调和线束.另一直线截调和线束，则截得的四点A′，C′，B′，D′仍成调和点列.

直线OA，OC，OB，OD的斜率分别记为k1，k2，k3，k4，则满足2（k1k3+k2k4）=（k1+k3）（k2+k4）.特别地，当调和线束四条直线中有一条直线如OD的斜率不存在时，调和线束的斜率满足k1+k3=2k2；当有一条直线的斜率为0，如k4=0时，调和线束的斜率满足1k1+1k3=2k2（调和线束斜率的等差模型）.

3题目探究与推广

统计了2020年到2024年近五年来全国卷关于极点极线问题的考查情况如表1，可以发现极点极线为背景的圆锥曲线问题是高考数学不折不扣的热点问题，借助GGB对其常见的四种考查形式进行探究与推广.

3.1定点问题

例1（2020年全国Ⅰ卷理/文·20/21）已知A，B分别为椭圆E：x2a2+y2=1（a>1）的左、右顶点，G为E的上顶点，AG·GB=8，P为直线x=6上的动点，PA与E的另一交点为C，PB与E的另一交点为D.

（1）求E的方程；

（2）求证：直线CD过定点.

极点极线背景分析：易得椭圆的方程为x29+y2=1，如图4，设AB与CD交于点M，CB与AD交于点Q，则△PQM为自极三角形，点M和直线PQ是一对极点极线.设点M的坐标为（xM，0），则直线PQ为x=9xM，又因为点P在直线x=6上，所以9xM=6，解得xM=32，所以直线CD恒过定点（32，0）.

探究1已知A，B分别为椭圆E：x2a2+y2b2=1（a>b>0）的左、右顶点， P为直线x=m（m>a）上的动点，PA与E的另一交点为C，PB与E的另一交点为D，直线CD过定点（a2m，0）（直线过定点与圆锥曲线的形状无关）.

如图5，设置数值滑动条a，b，m，区间范围分别为［0，5］，［0，a］，［a，10］，绘制椭圆E：x2a2+y2b2=1；设置点P（m，0），PA与E的另一交点为C，PB与E的另一交点为D；对直线CD开启跟踪，改变P点位置，可以发现直线CD随着P点的变化而变化，但是CD始终过定点；拖动滑动条改变a，b，m的值重复操作，发现直线CD仍然始终过定点，说明该性质与圆锥曲线的形状无关.

探究2 已知A，B分别为双曲线E：x2a2－y2b2=1的左、右顶点， P为直线x=m（0<m<a）上的动点，PA与E的另一交点为C，PB与E的另一交点为D，直线CD过定点（a2m，0）（以双曲线为例，直线过定点与圆锥曲线的类型无关）.

如图6，设置数值滑动条a，b，m，区间范围分别为［0，5］，［0，5］，［0，a］，绘制双曲线C：x2a2－y2b2=1；设置点P（m，0），PA与E的另一交点为C，PB与E的另一交点为D，对直线CD开启跟踪，改变P点位置，可以发现直线CD随着P点的变化而变化，但是CD始终过定点；拖动滑动条改变a，b，m的值重复操作，发现直线CD仍然始终过定点，说明该性质与圆锥曲线的类型无关.

探究3 已知A，B分别为椭圆E：x2a2+y2b2=1（a>b>0）的左、右顶点， 过点（m，0）（0<|m|<a）的直线与E交于C，D两点，AC与BD交于点P，点P过定直线x=a2m（互换条件与结论问题变为定直线问题）.

如图7，设置数值滑动条a，b，m，区间范围分别为［0，5］，［0，a］，［－a，a］，绘制椭圆C：x2a2+y2b2=1；设置M（m，0），过点M的直线与E交于C，D两点，直线AC，BD交于点P；对点P开启跟踪，改变C点位置，可以发现P点随着直线CD的变化而变化，但是P点始终在一条定直线上；拖动滑动条改变a，b，m的值重复操作，发现P点仍然始终在一条定直线上，说明互换本题的条件与结论仍然成立.

3.2定线问题

将例1中圆锥曲线的类型改为双曲线，互换条件与结论将题目改为定直线问题，就可以得到2023年新课标Ⅱ卷圆锥曲线大题，该题和2020年全国Ⅰ卷圆锥曲线大题同出一源，背景相同，其探究推广略.

例2（2023年新课标Ⅱ卷·21）已知双曲线C的中心为坐标原点，左焦点为（－25，0），离心率为5.

（1）求C的方程；

（2）记C的左、右顶点分别为A1，A2，过点B（－4，0）的直线与C的左支交于M，N两点，M在第二象限，直线MA1与NA2交于点P，证明：点P在定直线上.

极点极线背景分析：易得双曲线的方程为x24－y216=1，如图8，设MN与A1A2交于点B，设MA2与NA1交于点Q，则△PQB为自极三角形，直线PQ与点B互成一对极点极线，则点P在点B对应的极线x=－1上.

3.3平行垂直关系

例3（2024年全国甲卷理/文·20/21）设椭圆C：x2a2+y2b2=1（a>b>0）的右焦点为F，点M（1，32）在C上，且MF⊥x轴.

（1）求C的方程；

（2）过点P（4，0）的直线与C交于A，B两点，N为线段FP的中点，直线NB交直线MF于点Q，证明AQ⊥y轴.

极点极线背景分析：易得椭圆的方程为x24+y23=1.如图9，PA∩FM=D，点D在P的极线上，则A，D，B，P为调和点列，以Q为束心，QA，QD，QB，QP为调和线束.QD的斜率不存在，则kQA+kQP=2kQN，又N为PF的中点，可得kQB=kQN=2kQP，所以kQA=0，即AQ⊥y轴.

探究4设C：x2a2+y2b2=1（a>b>0）的右焦点为F，c=a2－b2，点M（c，b2a）在C上，过点P（a2c，0）的直线与C交于A，B两点，N为线段FP的中点，直线NB交直线MF于点Q，则AQ⊥y轴（AQ⊥y轴与圆锥曲线的形状无关）.

如图10，使用GGB作图，设置数值滑动条a，b，区间范围分别为［0，5］，［0，a］，绘制椭圆C：x2a2+y2b2=1；令c=a2－b2，设置F（c，0），M（c，b2a），P（a2c，0），N为线段FP的中点，过点P的直线与C交于A，B两点，直线NB交直线MF于点Q，连接线段AQ；对直线AQ开启跟踪，改变A点位置，可以发现直线AB、点Q随着A点的变化而变化，但是直线AQ始终垂直于y轴；拖动滑动条改变a，b的值重复上面操作，发现直线AQ仍然垂直于y轴，说明该性质与圆锥曲线的形状无关.

探究5设C：x2a2－y2b2=1（a，b>0）的右焦点为F，点M（c，b2a）在C上，过点P（a2c，0）的直线与C交于A，B两点，N为线段FP的中点，直线NB交直线MF于点Q，则AQ⊥y轴（以双曲线为例，探究AQ⊥y轴与圆锥曲线的类型无关）.

如图11，使用GGB作图，设置数值滑动条a，b，区间范围分别为［0，5］，［0，5］，绘制双曲线C：x2a2－y2b2=1；设置F（c，0），M（c，b2a），P（a2c，0），N为线段FP的中点，过点P的直线与C交于A，B两点，直线NB交直线MF于点Q，连接线段AQ；对直线AQ开启跟踪，改变A点位置，可以发现直线AB、点Q随着A点的变化而变化，但是直线AQ始终垂直于y轴；拖动滑动条改变a，b的值重复上面操作，发现直线AQ仍然垂直于y轴，说明该性质与圆锥曲线的类型无关.

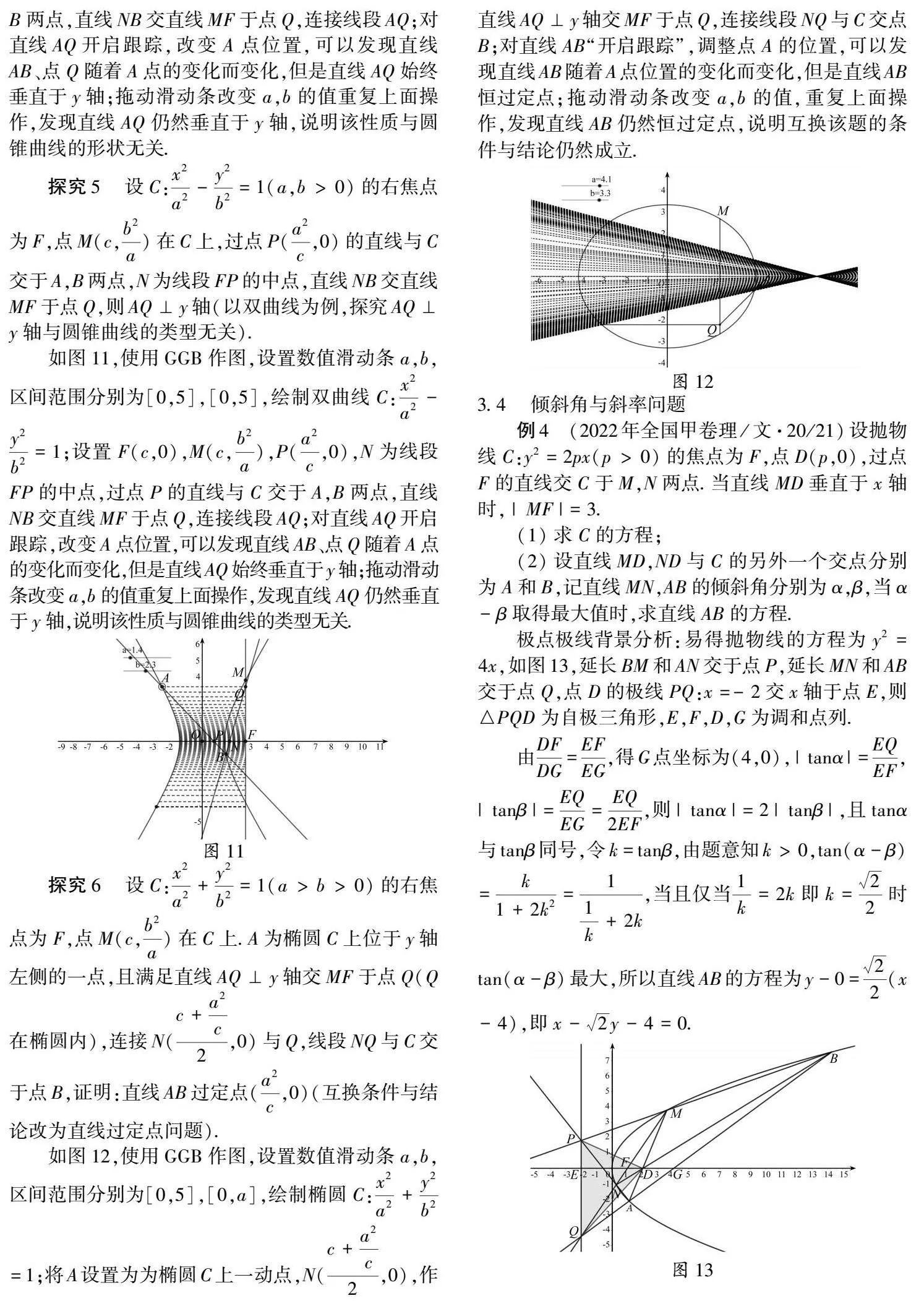
探究6设C：x2a2+y2b2=1（a>b>0）的右焦点为F，点M（c，b2a）在C上.A为椭圆C上位于y轴左侧的一点，且满足直线AQ⊥y轴交MF于点Q（Q在椭圆内），连接N（c+a2c2，0）与Q，线段NQ与C交于点B，证明：直线AB过定点（a2c，0）（互换条件与结论改为直线过定点问题）.[HJ1.3mm]

如图12，使用GGB作图，设置数值滑动条a，b，区间范围分别为［0，5］，［0，a］，绘制椭圆C：x2a2+y2b2=1；将A设置为为椭圆C上一动点，N（c+a2c2，0），作直线AQ⊥y轴交MF于点Q，连接线段NQ与C交点B；对直线AB“开启跟踪”，调整点A的位置，可以发现直线AB随着A点位置的变化而变化，但是直线AB恒过定点；拖动滑动条改变a，b的值，重复上面操作，发现直线AB仍然恒过定点，说明互换该题的条件与结论仍然成立.

3.4倾斜角与斜率问题

例4（2022年全国甲卷理/文·20/21）设抛物线C：y2=2px（p>0）的焦点为F，点D（p，0），过点F的直线交C于M，N两点.当直线MD垂直于x轴时，|MF|=3.

（1）求C的方程；

（2）设直线MD，ND与C的另外一个交点分别为A和B，记直线MN，AB的倾斜角分别为α，β，当α－β取得最大值时，求直线AB的方程.

极点极线背景分析：易得抛物线的方程为y2=4x，如图13，延长BM和AN交于点P，延长MN和AB交于点Q，点D的极线PQ：x=－2交x轴于点E，则△PQD为自极三角形，E，F，D，G为调和点列.

由DFDG=EFEG，得G点坐标为（4，0），|tanα|=EQEF，|tanβ|=EQEG=EQ2EF，则|tanα|=2|tanβ|，且tanα与tanβ同号，令k=tanβ，由题意知k>0，tan（α－β）=k1+2k2=11k+2k，当且仅当1k=2k即k=22时tan（α－β）最大，所以直线AB的方程为y－0=22（x－4），即x－2y－4=0.

探究7抛物线C：y2=2px的焦点为F，点D（p，0），过点F的直线交C于M，N两点，直线MD，ND与C的另外一个交点分别为A和B，直线AB过定点（2p，0）（定点问题）.

如图14，使用GGB作图，设置数值滑动条p，区间范围设为［－5，5］，绘制抛物线C：y2=2px；设置点D（p，0），过点F的直线交C于M，N两点，直线MD，ND与C的另外一个交点分别为A和B；对直线AB“开启跟踪”，调整点M的位置，可以发现直线AB随着点M位置的变化而变化，但是直线AB恒过定点；拖动滑动条改变p的值，重复上面操作，直线AB仍然恒过定点.

探究8抛物线C：y2=2px的焦点为F，点D（p，0），过点F的直线交C于M，N两点，直线MD，ND与C的另外一个交点分别为A和B，MN和AB的交点为P，AN和BM的交点为Q，点P，Q在定直线x=－p上（定直线问题）.

如图15，使用GGB作图，设置数值滑动条p，区间范围设为［－5，5］，绘制抛物线C：y2=2px；直线MN和AB的交点为P，AN和BM的交点为Q，对点P，Q“开启跟踪”，调整点M的位置，可以发现P，Q在定直线上；拖动滑动条改变p的值重复上面操作，P，Q仍在定直线上.

探究9抛物线C：y2=2px的焦点为F，点D（p，0），过点F的直线交C于M，N两点，直线MD，ND与C的另外一个交点分别为A和B，过点A和B作抛物线的切线，两条切线的交点在定直线x=－2p上（定直线问题）.

如图16，使用GGB作图，设置数值滑动条p，区间范围设为［－5，5］，绘制抛物线C：y2=2px；过点A和B作抛物线的切线，两条切线的交点为P；对点P“开启跟踪”，调整点M的位置，可以发现点P在定直线上；拖动滑动条改变p的值重复上面操作，P仍在定直线上.

探究10抛物线C：y2=2px的焦点为F，点D（p，0），过点F的直线交C于M，N两点，直线MD，ND与C的另外一个交点分别为A和B，以AB为直径的圆过原点（圆过定点问题）.

如图17，使用GGB作图，设置数值滑动条p，区间范围设为［－5，5］，绘制抛物线C：y2=2px；以AB为直径作圆，对圆“开启跟踪”，调整点M的位置，可以发现以AB为直径的圆恒过原点；拖动滑动条改变p的值重复上面操作，以AB为直径的圆仍然恒过原点.

5结束语

高考压轴题并非无源之水，而是有根可寻，极点极线蕴含着丰富的内容，是考试考查的重点，是命题取之不尽的源泉.借助GGB软件对复杂的几何动态问题进行展示探究，使得圆锥曲线问题的探究更加动态直观形象，进而窥探问题的背景，挖掘试题的本质，自然可以居高临下地认识高考试题，游刃有余地驾驭课堂[2].

参考文献

[1]王文彬.极点、极线与圆锥曲线试题的命制[J].数学通讯，2015（08）：62-66.

[2]张志勇.2016年高考四川卷解析几何题的探源与推广[J].中国数学教育，2017（18）：53-58.

作者简介

朱树金（1997—），男，山东滨州人，高中二级教师；主要从事数学课程与教学论研究.

李怡泉（1995—），男，湖北宜昌人，中学数学教师；主要从事数学课程与教学论研究.