高中数学课堂融入数学建模活动的策略探究
2024-11-05李江鹏
【摘要】在当前的高中数学教学实践中,部分学生难以将抽象的数学知识与现实生活中的问题有效结合,导致数学应用能力不足.针对这一问题,文章对数学建模的完整流程进行细致的拆解,并结合湘教版高中数学必修第二册“6.4数学建模案例(二):曼哈顿距离”这一知识点,详细阐述将数学建模活动融入高中数学课堂的具体策略:一是创设情境,提出具有现实意义的建模问题;二是引导学生分析问题,构建相应的数学模型;三是指导学生求解模型,并检验模型的有效性;四是将模型应用于实际,解决具体的数学问题,力图提供一套可操作性强、注重实效的数学建模教学策略,从而丰富高中数学课堂、培养学生综合运用数学知识解决复杂问题的能力.
【关键词】数学建模;高中数学;“曼哈顿距离”
引 言
在当今快速变化的信息时代,数学教育的目标早已超越单纯的知识传授,转向培养学生的创新思维、问题解决能力和实践应用能力.然而,传统的高中数学教育存在侧重于公式的记忆与应用,忽视数学与现实世界的紧密联系的问题,导致学生难以体会到数学的实际价值与魅力.这种理论与实践之间的鸿沟,不仅限制了学生对数学的深层次理解,也降低了学生解决复杂问题的能力,使其在面对跨学科挑战时显得力不从心.为了弥补这一教育短板,近年来,数学建模作为一种有效的教学手段,逐渐受到了教育工作者的重视.《普通高中数学课程标准(2017年版2020年修订)》也指出,通过高中数学的系列课程学习,学生应能够在现实世界中发现问题、提出问题,学会通过数学建模来解决实际问题,以落实核心素养的培养.此处的“数学建模”,就是将现实问题转化为数学语言的过程,它要求学生不仅要掌握数学知识,还要学会运用这些知识去理解和解决实际问题.这一过程不仅能够锻炼学生的逻辑思维和创新能力,还能提高学生的团队协作与沟通能力,为其未来的学术研究和职业生涯打下坚实的基础.
一、数学建模流程拆解
数学模型是对一类实际问题或实际系统发生的现象运用数学符号体系表示的一种(近似的)描述.在正式展开数学建模之前,首先要对需要解决问题的实际背景和内在机理进行深刻的了解,即“通过适当的调查和研究所解决的问题是什么?所要达到的主要目的是什么?”在此基础上,将数学建模流程拆解为假设、建立、求解、分析与检验、应用等核心环节,以实现对问题的深入剖析和精确求解.数学建模流程如图1所示.

模型准备完毕后,通过对问题本质的深入挖掘,找出问题的核心要素,以筛选出对问题解决起到关键作用的主要因素.针对问题的具体特点,进行合理的抽象处理,去除不必要的细节,并运用数学语言提出恰当的假设.随后,紧密贴合问题特征,区分常量与变量、已知与未知,使用数学工具将问题转化为数学语言,量化各个变量之间的关系.
构建数学模型之后,再针对不同类型的数学模型,采用相应的求解方法.模型求解的目标是找到问题的最优解或满意解,为实际问题的解决提供理论依据.为了验证所建模型的有效性,结合实际数学问题,对模型求解的数值结果进行数学分析.如果发现模型预测与实际情况存在显著偏差,而建模和求解步骤又都正确无误,那么问题往往出在模型的假设环节.此时,就需要回溯到建模的早期阶段,对那些可能不够准确或不切实际的假设进行重新审视和修正.通过这样反复验证、分析和修正,逐步剔除模型中的不合理因素,增强其适用性和可靠性,使数学模型不仅能够在理论上自洽,更能够在实践中有效地指导问题的解决,为实际问题的决策提供科学、精确的支持.
二、高中数学课堂融入数学建模活动的具体策略———以“曼哈顿距离”模型为例
(一)创设情境,提出建模问题
在高中数学课程中,空间几何部分因其抽象性和复杂性,常常成为学生学习的“拦路虎”.部分学生在面对空间几何问题时,往往束手无策,只能死记硬背公式和定理.为了改变这一现状,教师在教学过程中创设情境显得尤为重要.而创设情境的目的在于,让学生在解决实际问题的过程中,自然而然地运用数学知识,而不是单纯地记忆公式和定理.通过这样的教学策略,学生不仅能够掌握“曼哈顿距离”这一数学概念,更重要的是,学生能够意识到将数学应用于现实世界的意义,增强数学学习的趣味性和意义感.
为了让学生更好地理解几何概念,教师可以从日常生活中寻找素材,创设一个生动且贴近学生经验的情境,让“曼哈顿距离”的概念自然而然地浮现.例如,教师可以构建一个城市规划的情境:假设学生被邀请参与设计一座未来城市的交通网络,其中一条街道系统采用了曼哈顿网格布局,即所有街道都是正交的,要么南北向,要么东西向.
考虑到高中生已经具备一定的抽象思维能力和操作技能,教师可以灵活利用地图软件或地理信息系统(GIS)工具,让学生在电子地图上自主标记出起点和终点,并通过拖动、缩放等操作,细致地研究每一条路径的走向.“曼哈顿距离”示意图如图2所示.
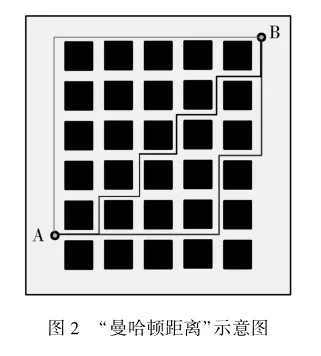
通过在电子地图上直观地观察不同路径的走向,学生能够更加深刻地理解路径规划背后的数学原理.在这个过程中,学生能够发现,假设普通人要从一个街区A走到另一个街区B,那就只能绕着建筑物走.那么,学生就会自然而然地思考:“如何计算从一个街区A到另一个街区B的步行距离?”这时,教师就可以适时引入“曼哈顿距离”这一概念,通过将抽象的数学概念嵌入具体的生活场景中,使学生更为直观地理解“曼哈顿距离”的含义,即两点之间的水平和垂直距离之和.随后,教师可以进一步深化情境,引入城市紧急救援服务等实际问题,引导学生思考“在发生紧急情况时,救护车需要从医院出发前往事故现场,如何选择最短路线?”这一问题.这种情境的设定,不仅能够引导学生主动提出建模问题,还可培养其解决复杂问题的综合技能.
(二)分析问题,构建数学模型
在数学建模过程中,当教师抛出一个具体的建模问题,如计算两点间沿网格行进的最短距离时,接下来就需要细致地指导学生如何运用精确的数学语言来描述这个问题.具体而言,学生需要将现实生活中复杂的街区布局抽象化,将其转化为一个简化的数学模型.换言之,就是将每个街区看作平面直角坐标系中的一个独立点,而连接这些街区的街道则对应于坐标轴上的线段.
通过这样的转化,原本纷繁复杂的街区距离问题变得清晰起来.学生现在面对的是一个在坐标系中计算两点之间距离的问题.在这个过程中,学生需要深入理解坐标系的构建原理,明确每个点在坐标系中的位置,以及如何通过坐标轴上的距离来表示实际街区之间的距离.这样一来,原本看似难以入手的实际问题,就变成了一个可以通过数学方法精确求解的数学问题.
例如,教师可以为学生提供一道例题:“某地三个新建居民区的位置分别位于三点D(3,20),E(-10,0),F(14,0),计划在x轴上方区域(包括x轴)内的某一点M处修建一个体育馆,试确定点M的位置,使其到三个居民区的‘曼哈顿距离’最小.”在学生阅读完题目后,教师需要适时引导学生回顾平面直角坐标系的相关知识,并鼓励学生绘制本道例题的坐标系配图,将居民区D,E,F的位置在图上标出,思考体育馆M可能的位置.坐标系配图如图3所示.

接下来,教师指导学生根据问题特点,构建数学模型.首先,让学生明确“曼哈顿距离”的定义:在平面直角坐标系中,两点之间的“曼哈顿距离”等于这两点在x轴方向上的距离与y轴方向上的距离之和.然后,教师引导学生将实际问题中的街区坐标代入“曼哈顿距离”公式.设体育馆的位置为M(x,y),居民区到体育馆的距离为Z,得到式(1),从而建立数学模型.
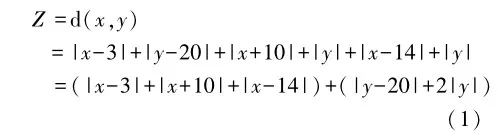
在这个过程中,教师要注意以下几点:(1)强调数学模型的合理性,确保模型能够准确地反映实际问题;(2)引导学生关注模型中的变量和参数,理解它们在实际问题中的意义;(3)鼓励学生运用数学知识,如坐标系、距离公式等,进行模型构建.通过这样的教学策略,学生不仅能够掌握“曼哈顿距离”的数学模型,还能够学会如何将实际问题抽象化,用数学的方法进行分析和解决.
(三)求解模型,检验模型效果

进一步,教师就可以引导学生利用绝对值的性质来求解X和Y的最小值.由此,学生可以推导出在水平方向上,当M点的横坐标x等于D点的横坐标3时,水平距离X达到最小值;同理,在垂直方向上,当M点的纵坐标y等于0时,垂直距离Y达到最小值.通过一步步的引导和计算,教师可鼓励学生总结出本题的答案:当体育馆的位置设定在点M(3,0)时,它到三个居民区的“曼哈顿距离”是最小的.
在完成模型的求解步骤后,教师应当指导学生进行模型效果的验证.学生需要将求得的点M(3,0)代入最初建立的“曼哈顿距离”模型中,通过计算得出该点到三个居民区的最小“曼哈顿距离”为44.为了进一步验证模型的准确性,学生可以随机选取其他几个坐标点,如(4,0),(3,1),(8,8)等,然后分别计算这些点到三个居民区的“曼哈顿距离”,并将计算结果与点M(3,0)的距离进行比较.
在这个过程中,教师可以引导学生记录下每一步的中间结果,以及最终得到的“曼哈顿距离”,这样的记录有助于在后续的验证环节中复查计算过程,确保没有遗漏或错误.通过比较这些计算结果,如果学生发现无论是M点附近的坐标还是较远位置的坐标,其“曼哈顿距离”都无一例外地大于44,那么就表明最初求解得到的点M(3,0)确实是使得“曼哈顿距离”最小的点,从而验证了模型的正确性和求解过程的准确性.
(四)结合实际,解决数学问题
模型分析与检验完成后,教师应当把握这个契机,继续拓展学生思维的深度和广度,不让教学活动就此停滞.具体而言,教师可以引导学生将模型的视角从课堂延伸至更加广阔的生活领域,提出与学生日常生活紧密相关的新问题.
一方面,教师应鼓励学生采用之前所构建的模型,来解决新的、类似的数学问题.例如,教师可以提出以下问题:“考虑到城市绿化带的布局,我们有一片绿化区域需要定期进行维护.该区域有三个维护站点P(2,8),Q(6,-4),R(-3,-2),以及一个资源中心S(0,0),现需要确定一条从资源中心出发,经过所有维护站点的最短巡回路径,以便高效地进行资源配送.请利用‘曼哈顿距离’模型来规划这条路径.”在这个问题中,学生不仅需要计算两点在同一象限内的距离,还要思考不同象限的正负坐标如何影响距离的计算.通过这种坐标点的变化,让学生更为直观地认识到,“曼哈顿距离”实际上是由横向和纵向距离的绝对值之和构成的,从而更深刻地领悟到“曼哈顿距离”的本质,以及在解决实际问题时如何灵活运用这一知识点.
另一方面,教师可以进一步拓展学生的思维,鼓励学生考虑现实问题中的多重变量.例如,教师可以引导学生探讨:“若要在城市中规划一条新的紧急救援路线,应如何考虑道路的宽窄、交通信号的设置,以及可能的障碍物等因素,以确保救援车辆能够快速且安全地到达目的地?”这要求学生在规划路径时,不仅要考虑最短距离,还要将安全因素纳入模型,考虑交通事故多发区域、易滑路面或施工区域等潜在的安全隐患,进而进行更为复杂的风险评估和路径规划.这种逐步深入的方式能够在提升学生数学应用能力的基础上,帮助学生树立正确的数学意识———在解决实际问题时,必须采取多角度、多模型的分析方法,这样才能得出更加全面和合理的解决方案,从而支持学生在未来的学习中,更加熟练地通过数学建模来解决实际问题.
结 语
综上所述,数学建模活动的融入,使得高中数学教学更加贴近实际,让学生在解决具体问题的过程中,自然而然地掌握数学知识,实现从知识传授到能力培养的转变.然而,要全面推广数学建模活动,使之成为高中数学教育的常态,仍要克服诸多挑战.高中数学教育应继续深化数学建模活动的融入,不断完善教学体系,创新教学方法.一方面,教师应继续提升自身对数学建模的认识,加强教学研究,积累更多成功案例;另一方面,学校和教育部门应加大对数学建模教学资源的投入,建立与之相适应的评价体系,为数学建模活动的深入开展提供保障.相信通过持续的努力与创新,高中数学教育将迎来一个更加充满活力与创造力的新篇章,让学生在数学的广阔天地里自由翱翔,用数学的语言描绘世界的无限可能.
【参考文献】
[1]蔡真逸.数学建模活动的课堂实践与思考:以沪教版“刹车距离”教学为例[J].高中数学教与学,2024(12):39-42.
[2]徐茵华.基于项目式学习开展高中数学建模活动和数学探究活动[J].青海教育,2024(4):40.
[3]闫伟.基于核心素养的高中数学建模教学实践与思考:以给定清水量漂洗衣服问题为例[J].教学考试,2024(11):58-63.
[4]李烁,夏宇晨,戴阔斌,等.基于高阶思维的高中数学建模活动课教学设计研究:以“消费券”模型为例[J].学周刊,2024(7):130-133.
[5]徐燕2b5f8a96fb960e9c80628b729a73f2848daa01a1edebd749cfc7f90a5463989a.基于核心素养的高中数学建模活动的实1c08ebbf454d4423b75f89772d94b0d89a1aed40bf84ffba1cea7935d5c31670践研究:以“茶水问题”为例[J].高考,2024(5):136-139.
[6]张文涛.核心素养导向的高中数学建模课程构建与实施[J].中国教育学刊,2024(2):1-8.
[7]徐金润,肖阳芳,邵贵明,等.深度学习理念下高中数学建模教学的设计与思考:以“鞋码与身高”为例[J].数学教学研究,2023,42(3):17-22,26.
[8]卢龙.“数学建模活动:测量学校内、外建筑物的高度”(第3课时)教学设计[J].中国数学教育,2023(8):53-60.
[9]李现勇.在数学知识的应用中提升学生的数学建模素养:以“生活中的三角函数”数学建模课为例[J].数学建模及其应用,2022,11(4):101-106.
[10]牛新荣.初中数学“综合与实践”活动研究:例谈建构主义学习环境下的初中数学建模活动[J].中学数学,2022(18):92-93.
