基于逆向重布线改进RRT-Connect算法的机械臂路径规划

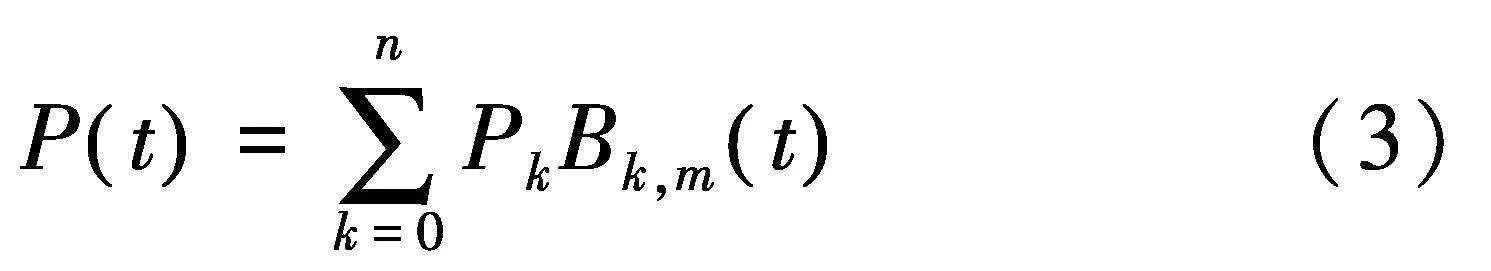
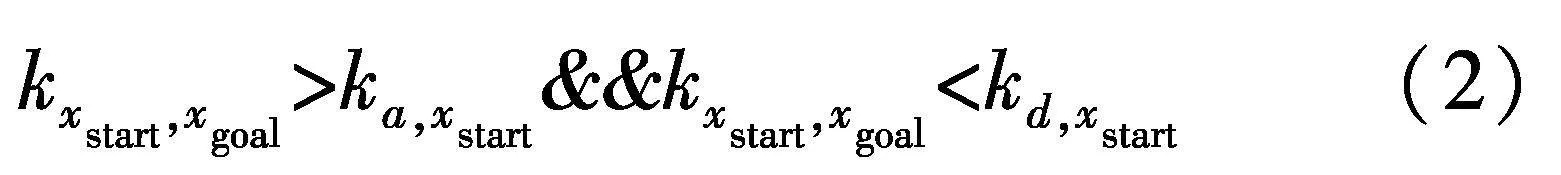
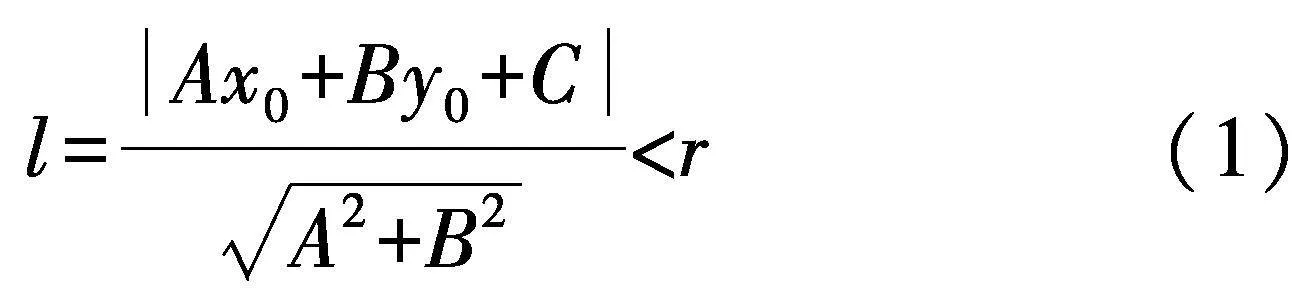
摘 要： 为解决RRT-Connect算法在复杂非结构环境下规划出的路径成本较长、有效节点数过多、曲折不平滑等问题，提出了一种基于逆向重布线的改进RRT-Connect算法（Improved-RRT-Connect）.首先，在算法的起始位置加入碰撞检测函数，当起点和终点之间不存在障碍物时，能够快速生成一条路径；其次，通过对生成的路径采取逆向重布线的措施，对生成的路径中的节点进行重新筛选布线，达到缩短生成路径长度，减少有效节点数量的目的；最后，通过结合B样条曲线对生成的路径进行拟合处理，得到一条平滑连续的路径.通过Improved-RRT-Connect算法与RRT、RRT*-Smart、RRT-Connect等算法的对比实验表明，在规划时间上，Improved-RRT-Connect算法比RRT、RRT*-Smart算法减少了52.14%、98.53%，在路径成本上比RRT、RRT-Connect算法减少了19.39%、17.15%，阐明了提出的Improved-RRT-Connect算法的优越性.

关键词： RRT-Connect算法；机械臂；碰撞检测；逆向重布线；B样条曲线

中图分类号：TP241.3"" 文献标志码：A"""" 文章编号：1673-4807（2024）02-047-06

Improved RRT-Connect algorithm based on reverserewiring for manipulator path planning

Abstract：In order to solve the problems of long path cost， excessive number of effective nodes and uneven twists and turns in complex unstructured environment， an improved RRT-Cconnect algorithm based on reverse rewiring is proposed. Firstly， a collision detection function is added to the starting position of the algorithm， which can quickly generate a path when there is no obstacle between the starting point and the ending point. Secondly， through the measures of reverse rewiring of the generated path， the nodes in the generated path are re-screened and routed， so as to shorten the length of the generated path and reduce the number of effective nodes. Finally， a smooth and continuous path is obtained by fitting the generated path with B-spline curve. The experimental results show that the planning time of the improved RRT-Connect algorithm is 52.14% and 98.53% less than that of RRT and RRT*-smart algorithms， respectively， and the path cost is reduced by 19.39% and 17.15%. The advantages of the improved-RRT-Connect algorithm proposed in this paper are illustrated.

Key words：RRT-Connect algorithm， manipulator， collision detection， reverse rewiring， B-spline curve

采摘机器人通常由机械臂和导航车组成，采摘主体为机械臂.采摘环境中存在诸多未知的静态和动态的不规则障碍物，所以如何给机械臂规划一条合适的运动轨迹，使其在该条路径上能够迅速无碰撞的采摘果实是机械臂采摘果实研究中的重中之重.

为了解决机械臂在多维空间中寻找最优路径解的问题，提出了基于搜索的路径规划和基于智能算法的路径规划，其中典型的算法有A*算法、人工势场法、蚁群算法、遗传算法等[1-2].A*算法是一种搜索式的路径规划算法，添加了启发式函数，减少了路径搜索的面积，文献[3-4]提出了改进的A*算法，解决了传统A*算法产生的锯齿路径和交叉路径中存在的节点多、距离远、转弯角度大的问题.文献[5-6]分别提出基于改进的预规划人工势场法和基于动态窗法（dynamic window approach，DWA）的改进有源滤波器方法，有效解决了机器人在传统人工势场法下容易陷入局部极小值的问题.文献[7]提出一种改进的自适应蚁群算法，有效的解决了原始蚁群算法寻找路径耗费时间长，路径解非最优的不足；文献[8]通过调整蚁群算法的合适参数以及添加与信息素相关的正弦函数克服了蚁群算法收敛时间长，容易陷入局部最优解的缺点.文献[9]提出了一种提高累积检测概率（cumulative detection probability，CDP）的改进遗传算法，该方法有效的提高了遗传算法的收敛速度和稳定性；文献[10]也对遗传算法进行了改进，有效的避免了遗传算法过早地找到非最优解路径，提高了遗传算法的全局搜索能力.

为了减少路径规划算法所消耗的时间，提出快速搜索随机树算法（rapidly-exploration random tree， RRT），RRT算法随机地在规划空间内采样，通过判断路径线段是否与障碍物产生交集，有选择的保留采样点，避免了对障碍物建模，相较于搜索算法和智能算法其效率较高.但RRT算法也存在一定的局限性，其原理是随机采样，故而在规划路径时具有一定的盲目性.为了解决以上问题，文献[11]为了简化空间的复杂度以及提高规划效率，提出1-0 Bg-RRT算法；文献[12]提出了一种基于三角不等式的改进RRT-Connect算法，有效地减少了规划所需要的时间和规划路径的成本；文献[13]提出了基于CTB-RRT*的规划算法，引入柯西函数有效地减少了采样点的数量，增加目标引力，有效地提高了局部区域的搜索速度；文献[14]为了提高RRT*的收敛速度，获得更优解，结合P-RTT*和Q-RRT*的优点，提出了PQ-RRT*算法.

RRT-Connect算法虽然相较于RRT算法规划路径所需要的时间更短，但由于过早地找到路径，往往所寻路径并非最优解，存在路径成本较长的问题，同时RRT-Connect算法规划出的路径是由多段子线条组成的折线，因此存在着路径曲折不平滑的问题.因此，文中提出了一种基于逆向重布线（reverse rewiring）的RRT-Connect改进算法（Improved-RRT-Connect），并对其生成的路径采用B样条曲线对其进行拟合.实验表明，所提出的Improved-RRT-Connect算法所生成的路径更短，也更加平滑.

1 RRT算法与RRT-Connect算法分析

1.1 RRT算法

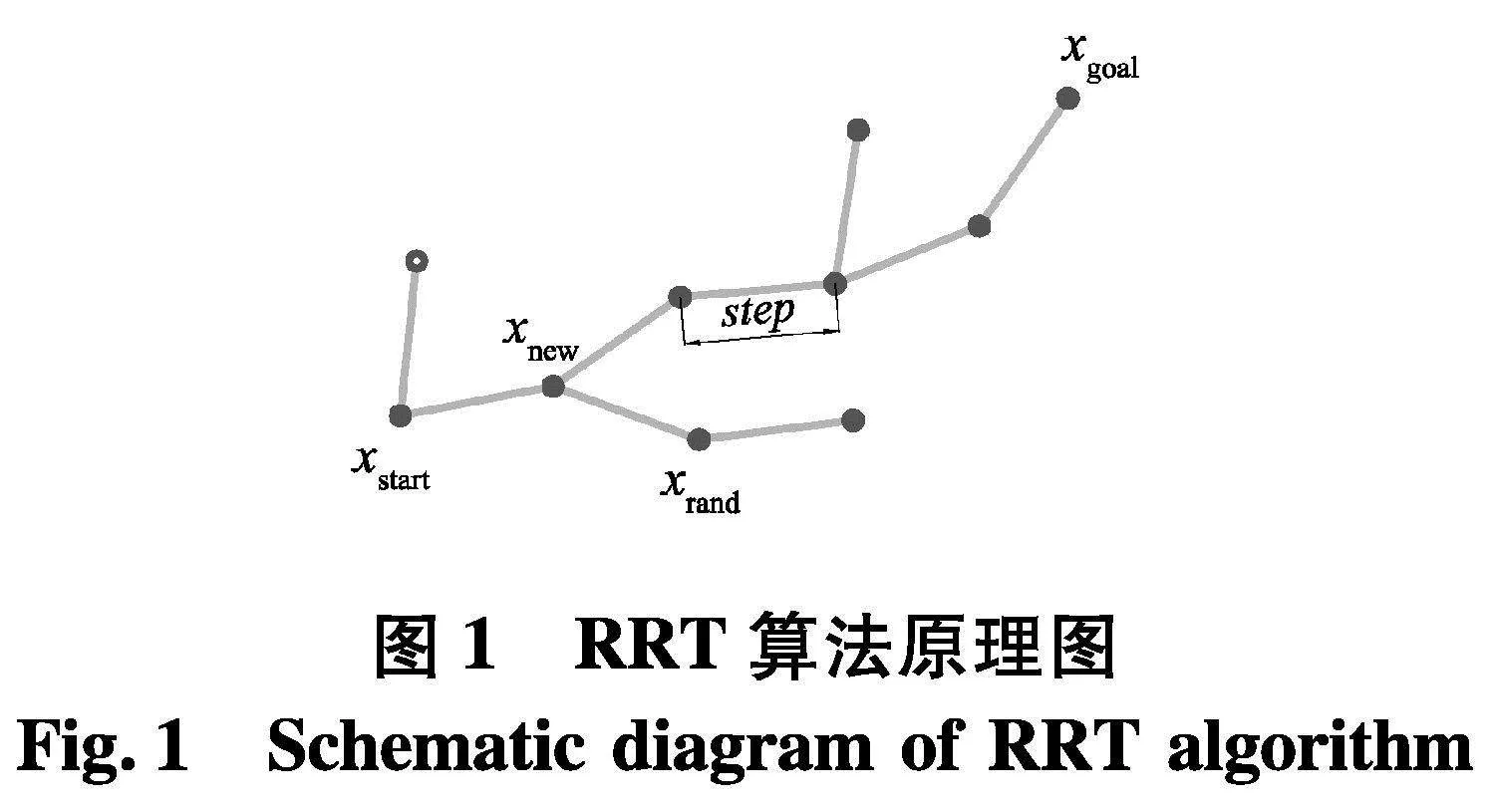
RRT算法的工作原理是对探索空间进行不断的采样，然后像树的生长过程一样不断扩张，每一个采样点都是下一个采样点的父节点，直到最终采样点为目标点时停止，RRT算法的搜索过程如图1.

生长树的扩张过程为：设置初始节点xstart和目标节点xgoal，同时初始节点即为生长树T的起点.随机产生一个节点xrand，计算xrand到生长树上各节点的距离，选择最短距离的节点作为xrand的最近节点xnearst.连接xrand与xnearst，该连线即为生长树的生长方向，在该生长方向上生成新的节点xnew，以步长step作为xnew到父节点xparent的距离（此时的xparent即为xstart），判断xnew与xparent的连线是否与障碍物发生交集，如果不相交则保留xnew并添加到生长树上，否则抛弃xnew，重新采样节点.每次产生新节点xnew后，判断xnew与xgoal的距离是否小于步长step，若小于步长且二者之间的连线未与障碍物发生碰撞，则直接将目标点xgoal作为生长树的终点，并输出找到的路径，否则重新进行采样.

1.2 RRT-Connect算法

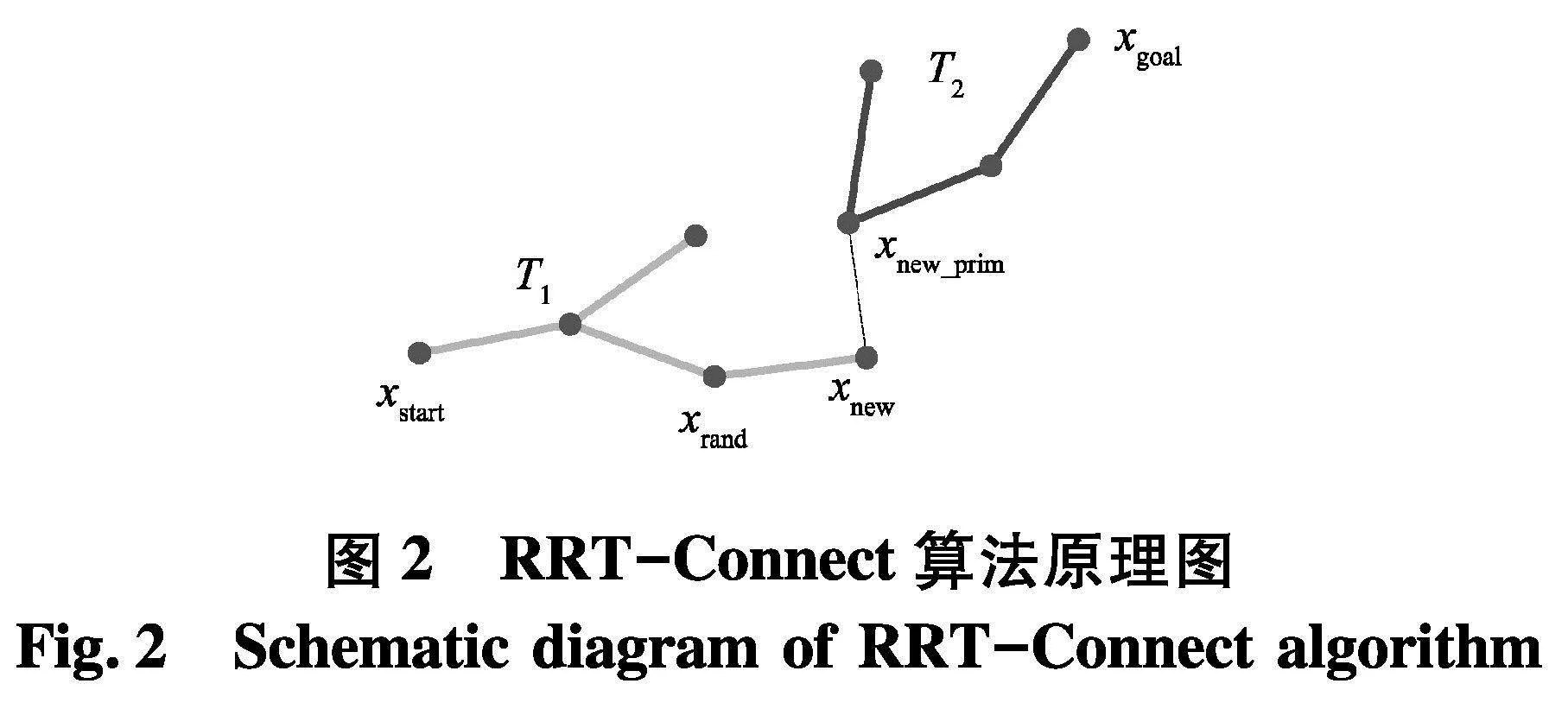
RRT-Connect算法不再遵循RRT算法单一地从起点扩展一棵生长树，而是从起点和终点分别扩展两棵生长树，当两棵树的终点重合时规划完成，同时在随机采样的过程中一棵树的生长方向总是以另外一棵树中最近的节点作为这棵树继续向外扩展的依据，当在这个方向上未遇到障碍物时则继续沿着这个方向扩展，当遇到障碍物时，则以另一个扩展树向外扩展，因此算法可以有效地走出寻找局部最优的困境.基于以上策略RRT-Connect算法在搜索速度上比RRT算法有着显著的提高.图2为RRT-Connect算法的原理图.

2 Improved-RRT-Connect算法

2.1 逆向重布线

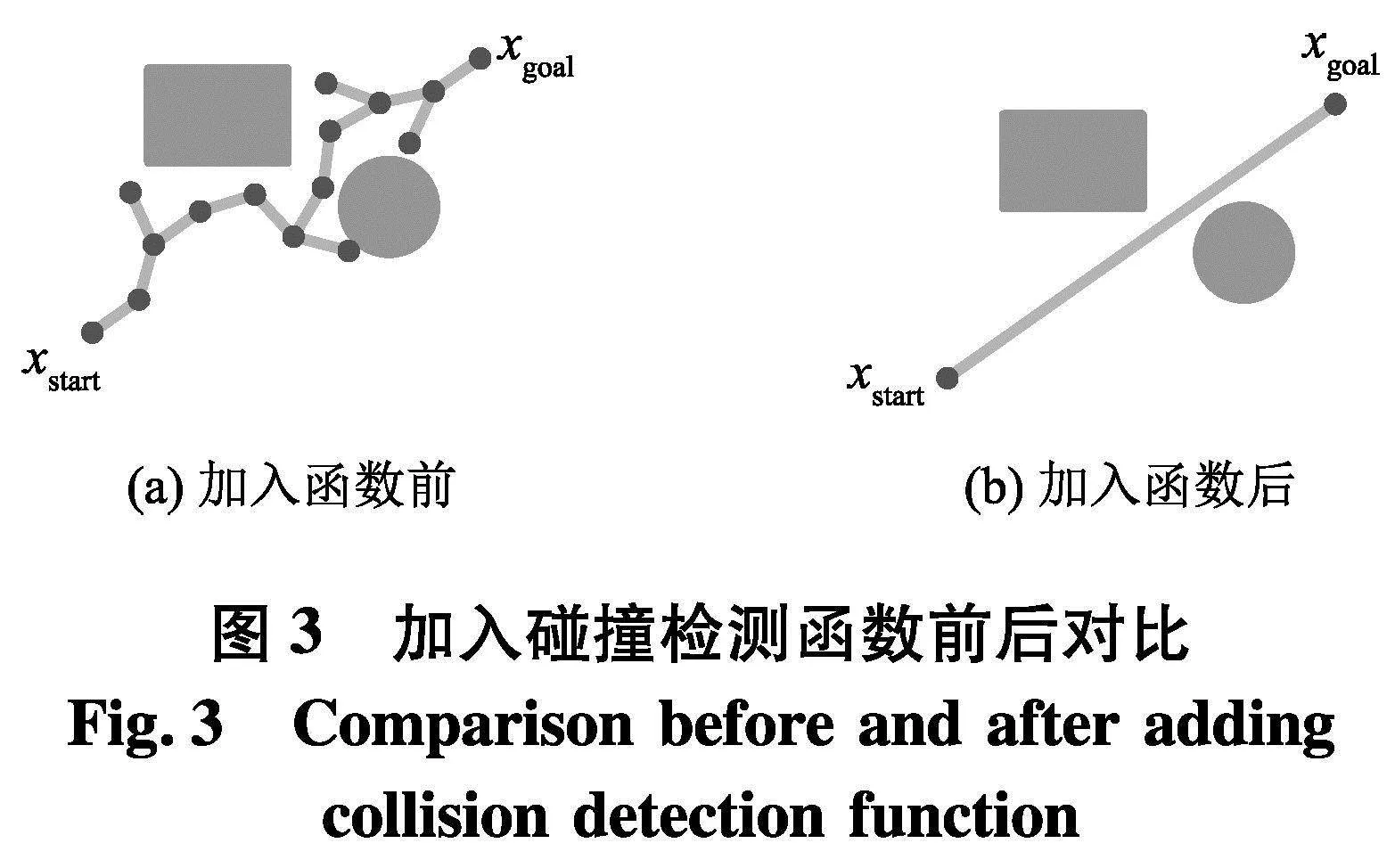
文中提出了一种基于逆向重布线的Improved-RRT-Connect算法.首先，在RRT-Connect算法的端部加入碰撞检测函数，因为RRT-Connect算法采样是随机的，即使起点到终点之间并不存在障碍物，该算法仍然会规划一条曲折的多线段组成的路径，如图3（a），而加入碰撞检测函数后，当起点到终点之间不存在障碍物时，则规划出一条从起点到终点的直线段，如图3（b）.

为方便描述，障碍物的形状设定为圆形和矩形.圆形障碍物判断碰撞条件为：

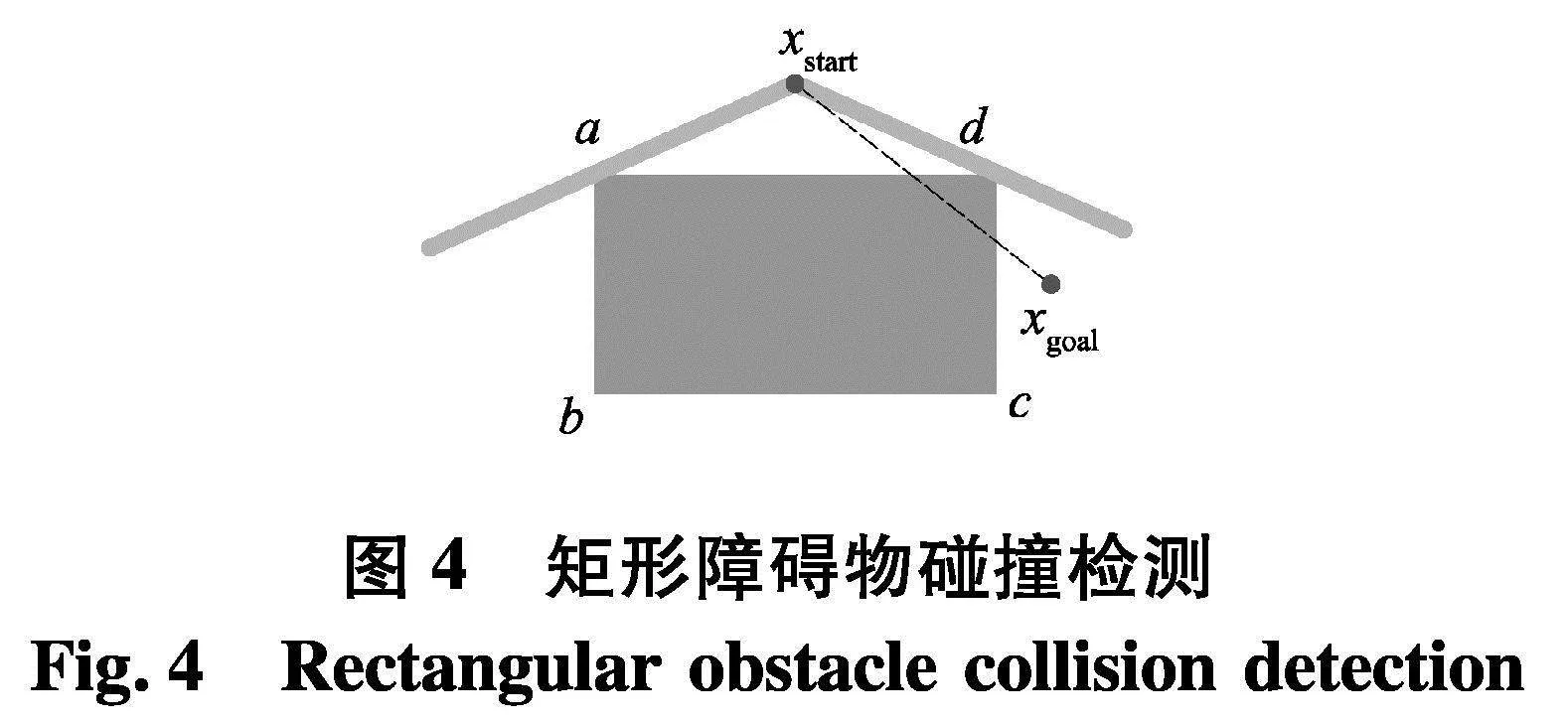
式中：l为障碍物中心点到直线的距离；A、B、C分别为起点和终点构成的直线方程系数；（x0，y0）、r分别为圆形障碍物的中心点坐标和半径；矩形障碍物判断碰撞条件为：

式中：k为直线的斜率，a、b、c、d为矩形顶点，如图4.

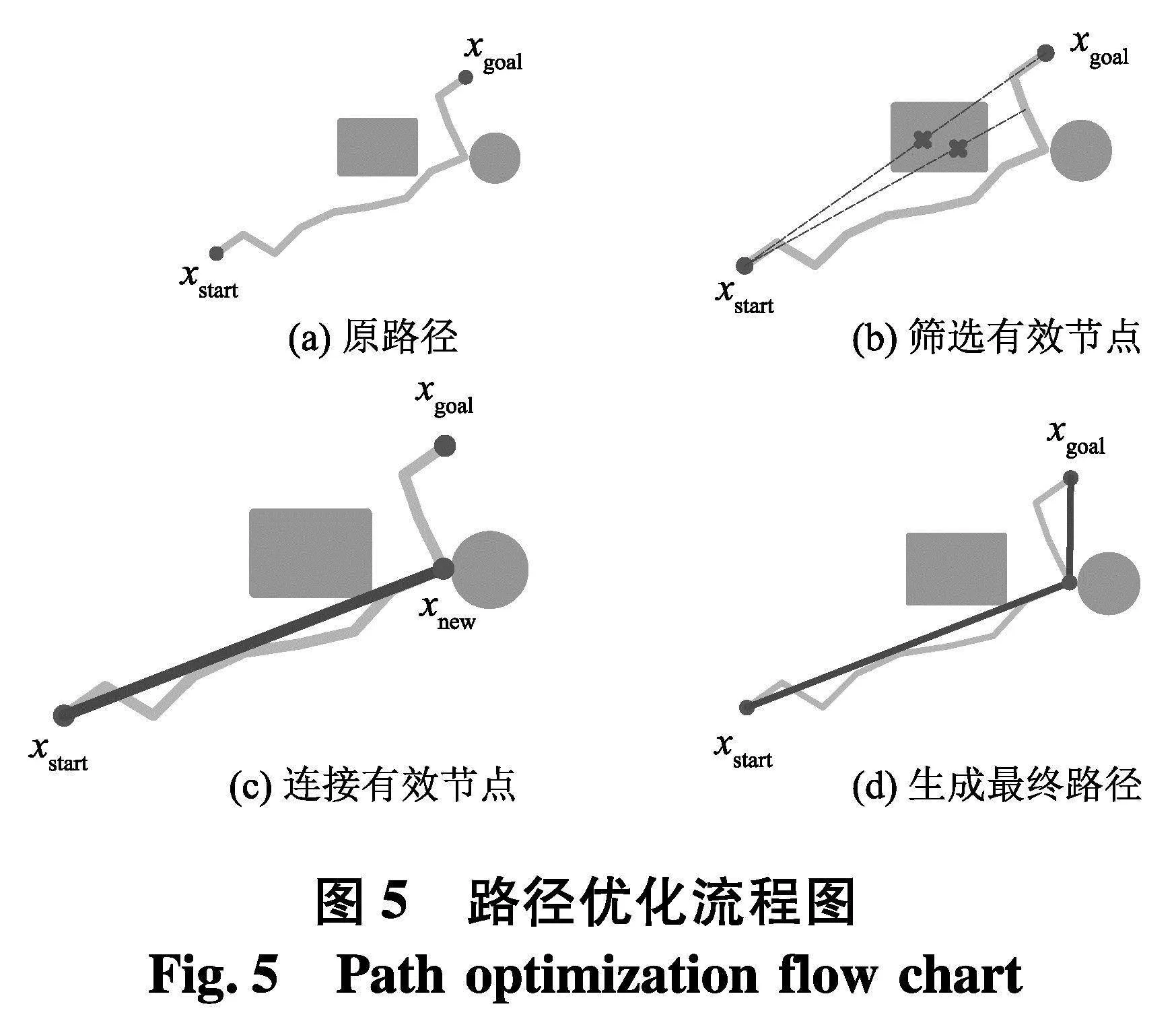
接着，当起点和终点之间存在障碍物时，继续使用RRT-Connect算法规划出一条路径.对于规划出的路径采用逆向重布线的方式对已生成的路径点进行重新筛选并连线.图5（a）为RRT-Connect算法规划出的路径；图5（b）表示以xstart为起点，从xgoal开始沿着xstart方向逐个寻找点与xstart连线，当连线与障碍物相交时，丢弃此连线；图5（c）表示寻找到点xnew与xstart连线未与障碍物发生碰撞，保留此路径段；图5（d）为以xnew为起点，从xgoal开始沿着xnew方向逐个寻找点与xnew连线，此时终点xgoal与xnew的连线未与障碍物发生碰撞，路径优化完成.

改进算法中修改的代码如表3.

2.2 B样条曲线平滑路径

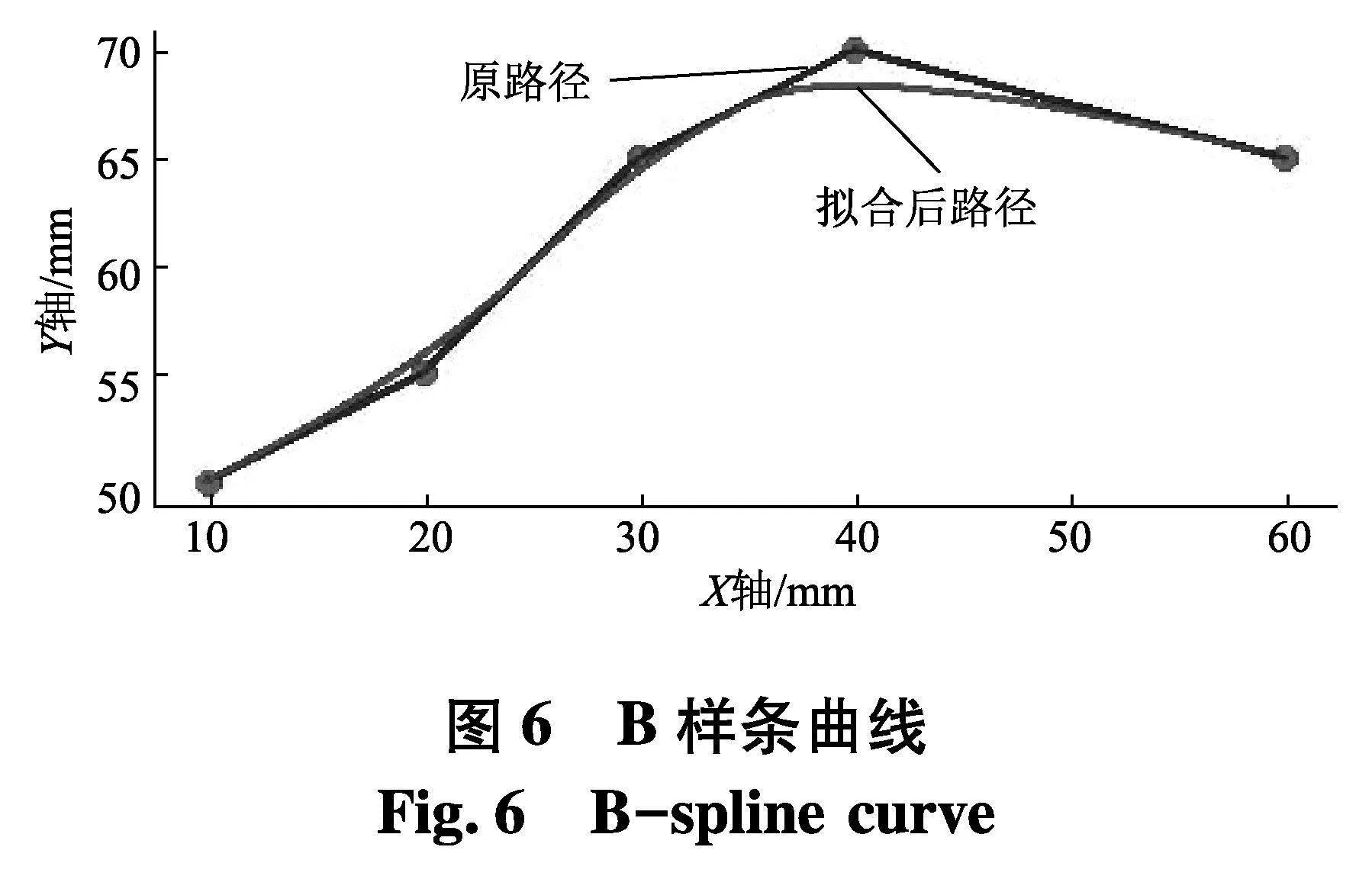
虽然利用逆向重布线的方法对RRT-Connect算法做出了改进，但改进后得到的路径仍是由多条线段组成的折线，因此在两条线段连接处可能是陡峭的，不平滑的，这将导致机械臂在运动到此处时会停顿重新更改方向移动增加运行时间，频繁的停顿和急速运动会加剧机械臂关节处的磨损，减少机械臂的使用寿命.针对上述问题，用B样条曲线对规划好的路径进行拟合处理，最终得出对机械臂运动友好的平滑路径.

B样条曲线具有良好的连续性，通常对生成曲线的局部控制点进行调整时，只有该区域的曲线会受到影响，其余区域的曲线将保持原样.此外，B样条曲线与多边形或多线段的逼近程度较好.文献[15-16]提出了基于B样条曲线对路径进行平滑处理的研究方法.文献[17]提出在样条函数中插入经济点，自动生成节点向量，有效解决了在拟合路径过程中与障碍物碰撞的问题.

B样条曲线的数学表达式为：

式中：Pk （k = 0， 1， 2， …，n）为第k个控制顶点，又称de Boor点；m为阶参数；t为归一化曲线长度参数.Bk，m（t）是B样条基函数，为k次分段多项式，由Cox-de Boor递归公式定义为：

3 实验验证和分析

文中比较了RRT算法、RRT*-Smart算法、RRT-Connect算法与所提出的Improved-RRT-Connect算法在复杂环境下的执行效率.通过在Python中使用Plotly构造具有障碍物的二维仿真环境，障碍物设置为一定数量的矩形和圆形，设置起点的坐标为（2，2），目标点坐标为（49，24），最大迭代次数为5 000，步长Step为0.8.搭载仿真环境的硬件设备CPU为：I7 - 6700HQ，主频为：2.60 GHz 四核，显卡为：NVIDIA GeForce 940MX，显存为：2 GB，主硬盘为：128 GB 固态硬盘，内存为：12 GB，操作系统为：Windows 10 Enterprise 64位.

3.1 逆向重布线验证

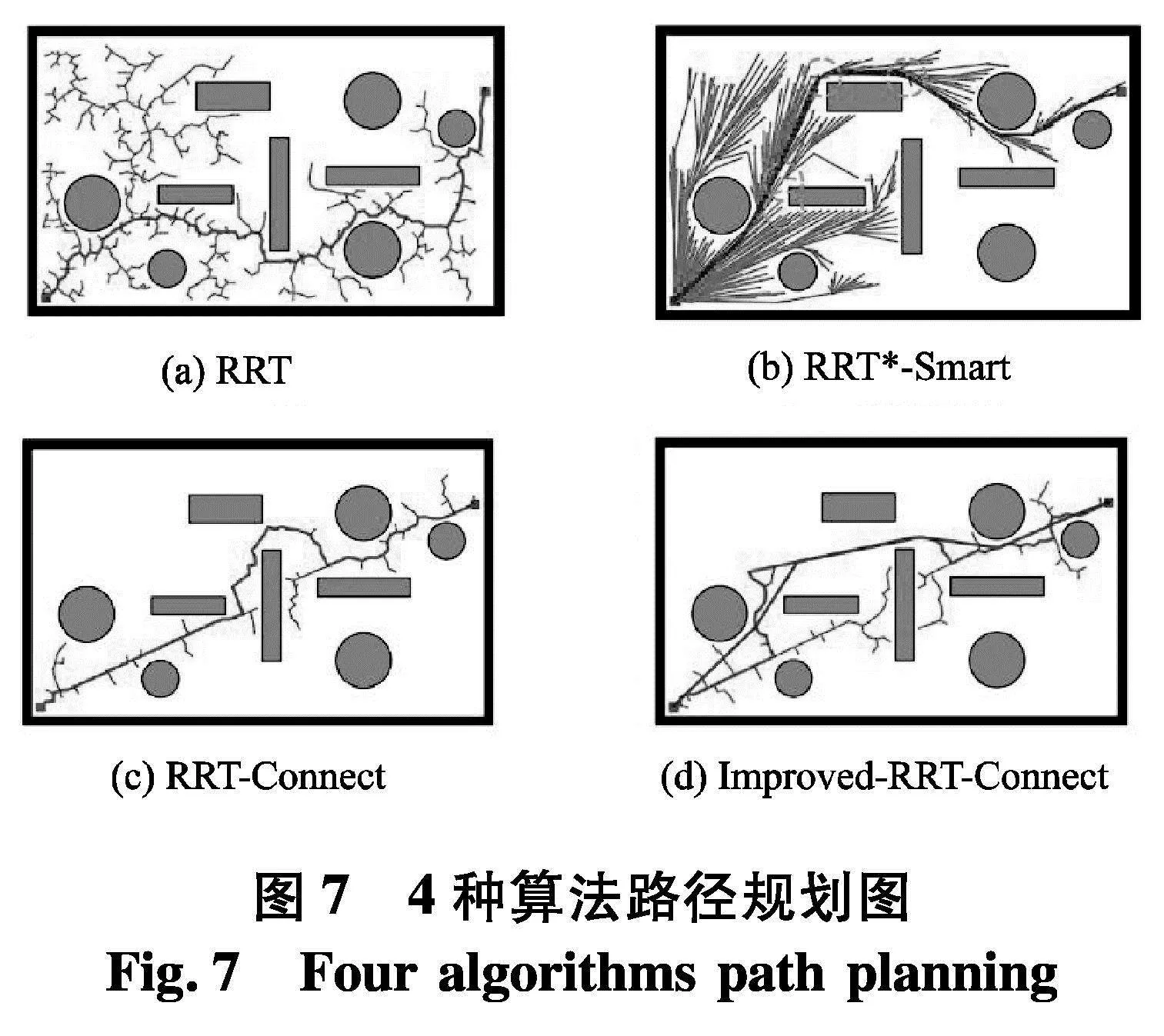
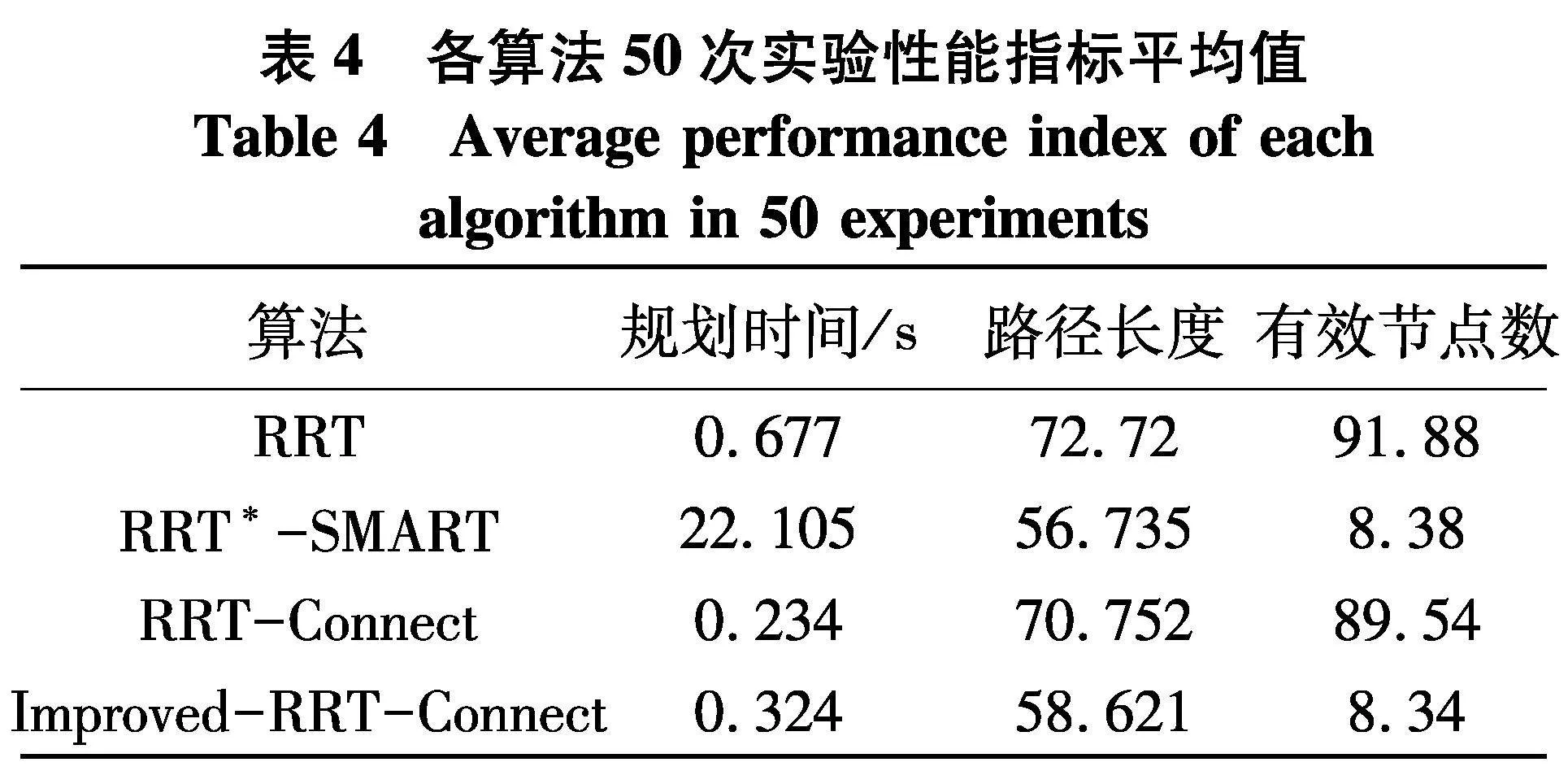
分别对4种算法进行50次实验，对各算法规划的时间和规划出的路径成本以及路径解中的节点数取平均值.图7展示了4种算法在仿真环境中规划路径的情形，图7中随机扩展的线条为各算法的采样过程，图7中连接起点和终点的线条为路径解.表4中列出了各个算法中的一些性能指标，包括路径规划所耗时间、路径规划的总成本、最终路径中的节点数.

从表4中可以得知Improved-RRT-Connect算法在时间和路径长度上的性能都优于RRT算法，在规划时间和路径长度上Improved-RRT-Connect算法比RRT算法分别减少了52.14%，19.39%.虽然Improved-RRT-Connect算法在规划路径的长度上略高于RRT*-Smart算法，但在规划时间上却大大低于RRT*-Smart算法，其减少的时间达98.53%.相较于RRT-Connect算法Improved-RRT-Connect算法在规划时间上性能稍逊，但不可否认其规划速度仍属快速，而在路径长度上Improved-RRT-Connect算法比RRT-Connect算法减少了17.15%.

综合考虑4种算法的性能指标，Improved-RRT-Connect算法优于RRT算法、RRT*-Smart算法和RRT-Connect算法.同时经过逆向重布线后的RRT-Connect算法，其路径解中的节点数更少，为B样条曲线平滑路径奠定良好基础.

3.2 B样条曲线拟合路径验证

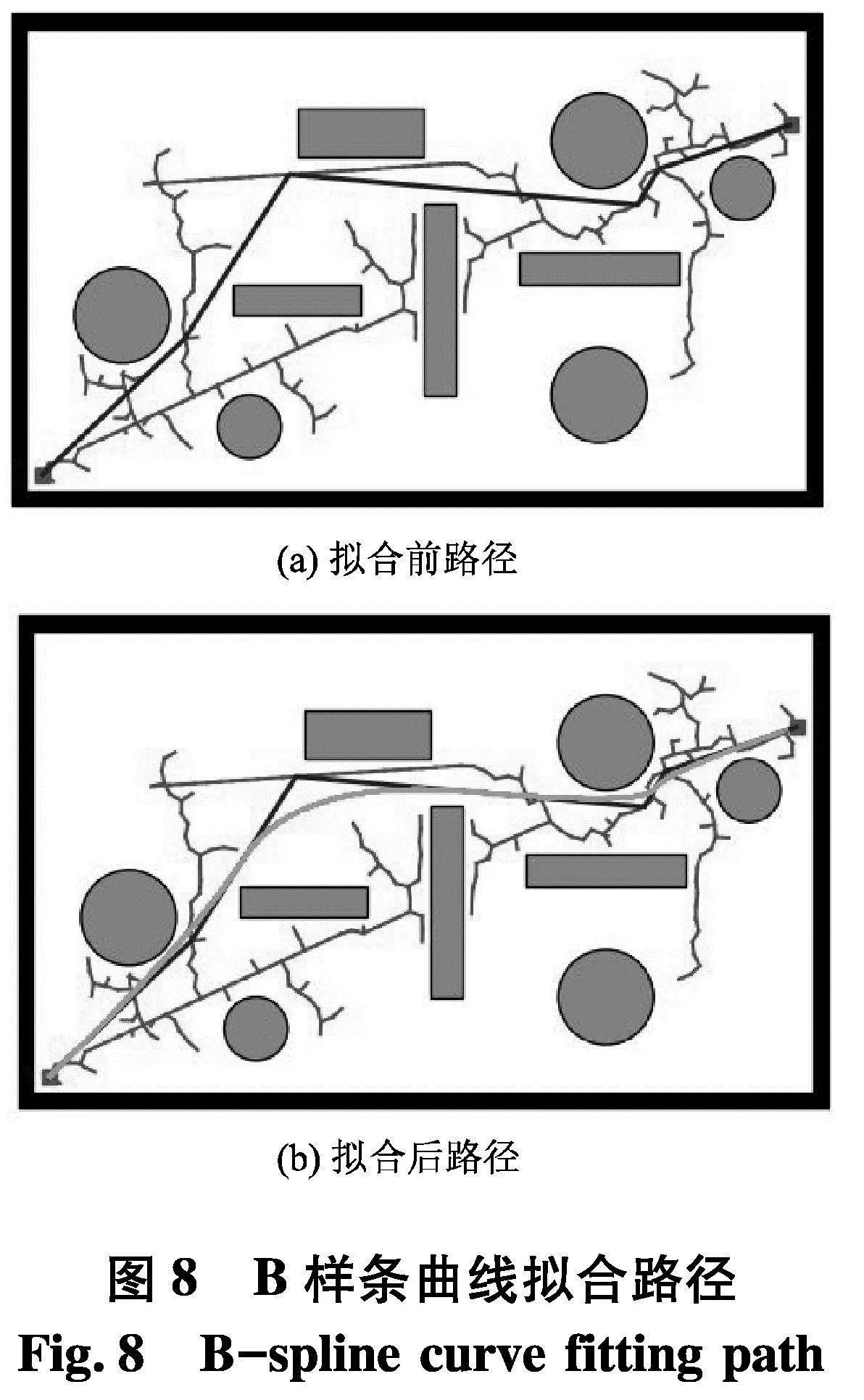
对改进算法规划出的路径进行平滑处理.规划出的路径是由多段线段组成的路径，在用B样条曲线对路径进行拟合处理时，将每段线段的端点作为B样条曲线的控制点，如图8.

通过采用B样条曲线对原曲折路径进行拟合处理，避免了拼接处不连续的问题，最终生成一条有利于机械臂运动的路径.

4 结论

为进一步提高RRT-Connect算法的搜索效率，减少所规划路径的长度，文中结合逆向重布线理论在RRT-Connect算法采取了进一步的改进，提出了Improved-RRT-Connect算法.具体改进方法如下：

（1） 在算法的起始位置加入碰撞检测函数，当起点和终点之间不存在障碍物时，能够快速生成一条路径.

（2） 通过对生成的路径采取逆向重布线的措施，对生成的路径中的节点进行重新筛选，达到缩短生成路径长度，减少有效节点数量的目的.

（3） 通过结合B样条曲线对生成的路径进行拟合处理，得到一条平滑连续的路径.

为了验证改进算法的优越性，分别对RRT算法、RRT*-Smart算法、RRT-Connect算法和Improved-RRT-Connect算法进行了50次实验，并对结果取平均值，得出结论：

（1） 在规划时间上，Improved-RRT-Connect算法比RRT算法、RRT*-Smart算法分别减少了52.14%、98.53%.

（2） 在路径成本上比RRT算法、RRT-Connect算法分别减少了19.39%、17.15%.

（3） 改进后的路径规划算法生成的路径更加平滑连续.

参考文献（References）

［1］ 林韩熙，向丹，欧阳剑，等.移动机器人路径规划算法的研究综述[J].计算机工程与应用，2021，57（18）：38-48.

[2] 官金炫，林桂潮，张世昂，等.水果采摘机械臂避障运动规划优化算法[J].现代农业装备，2021，42（3）：49-55.

[3] TANG G， TANG C， CLARAMUNT C， et al. Geometric A-star algorithm： an improved A-star algorithm for AGV path planning in a port environment[J]. IEEE Access， 2021， 9： 59196-59210.

[4] LE A V， PRABAKARAN V， SIVANANTHAM V， et al. Modified a-star algorithm for efficient coverage path planning in tetris inspired self-reconfigurable robot with integrated laser sensor[J]. Sensors， 2018， 18（8）： 2585.

[5] SHEN H， LI P. Unmanned aerial vehicle （UAV） path planning based on improved pre-planning artificial potential field method[C]∥2020 Chinese control and decision conference （CCDC）. USA：IEEE， 2020： 2727-2732.

[6] HU J， CHENG C， WANG C， et al. An improved artificial potential field method based on DWA and path optimization[C]∥2019 IEEE International Conference on Unmanned Systems （ICUS）.USA： IEEE， 2019： 809-814.

[7] MIAO C， CHEN G， YAN C， et al. Path planning optimization of indoor mobile robot based on adaptive ant colony algorithm[J]. Computers amp; Industrial Engineering， 2021， 156： 107230.

[8] PAN C， WANG H， LI J， et al. Path planning of mobile robot based on an improved ant colony algorithm[C]∥International Conference on Convergent Cognitive Information Technologies. Cham： Springer， 2018： 132-141.

[9] GUO H， MAO Z， DING W， et al. Optimal search path planning for unmanned surface vehicle based on an improved genetic algorithm[J]. Computers amp; Electrical Engineering， 2019， 79： 106467.

[10] LI Y， HUANG Z， XIE Y. Path planning of mobile robot based on improved genetic algorithm[C]∥2020 3rd International Conference on Electron Device and Mechanical Engineering （ICEDME）. USA：IEEE， 2020： 691-695.

[11] GAN Y， ZHANG B， KE C， et al. Research on robot motion planning based on RRT algorithm with nonholonomic constraints[J]. Neural Processing Letters， 2021， 53（4）： 3011-3029.

[12] KANG J G， LIM D W， CHOI Y S， et al. Improved RRT-connect algorithm based on triangular inequality for robot path planning[J]. Sensors， 2021， 21（2）： 333.

[13] 张勤， 乐晓亮， 李彬， 等. 基于 CTB-RRT～*的果蔬采摘机械臂运动路径规划[J]. 农业机械学报， 2021，52（10）：129-136.

[14] LI Y， WEI W， GAO Y， et al. PQ-RRT*： An improved path planning algorithm for mobile robots[J]. Expert Systems with Applications， 2020， 152： 113425.

[15] CHIARAVALLI D， CALIFANO F， BIAGIOTTI L， et al. Physical-consistent behavior embodied in B-spline curves for robot path planning[J]. IFAC-Papers on Line， 2018， 51（22）： 306-311.

[16] 吕恩利， 阮清松， 刘妍华， 等. 基于动态识别区和 B 样条曲线的智能叉车避障路径规划[J]. 农业机械学报， 2019， 50（1）：359-366.

[17] NOREEN I. Collision free smooth path for mobile robots in cluttered environment using an economical clamped cubic B-spline[J]. Symmetry， 2020， 12（9）： 1567.