机械臂工作空间全局相对可操作度图的构建方法

李宪华+疏杨+张雷刚+郭帅+张军

摘要：针对机械臂工作空间的灵活性问题，提出了一种全局相对可操作度图的构建方法。该方法首先将机械臂工作空间进行网格化处理，得到离散位置；然后在离散位置的均布小球上建立直角坐标系，通过绕坐标轴旋转的方式完成机械臂姿态的离散；而后将每个离散位置上的位姿进行逆运动学解算，并计算得到该位置上的最大相对可操作度；最后采用可视化的方法绘制出机械臂工作空间的相对可操作度分布图，进而揭示机械臂在其工作空间内的灵活性分布规律。该方法为机械臂的设计提供了相关理论依据，为机械臂的任务操作规划奠定了基础。

关键词：机械臂；相对可操作度图；逆运动学

中图分类号：TP241文献标志码：A文章编号：1672-1098（2016）01-0056-06

Abstract：Aiming at the flexibility of manipulators in working space， a method of constructing global relative manipulability map was proposed. In this method， the working space of the manipulator was processed by grid， and the discrete positions were obtained； then the rectangular coordinate system was set up on the discrete positions， and the discrete positions of the manipulator were accomplished by rotating the coordinate axis； the position and pose of each discrete position were calculated by inverse kinematics， and the maximum relative operational degree of the position was calculated； finally， the visual method was used to draw the relative operational degree distribution map of the manipulator in the working space to reveal the flexibility distribution of the manipulator in its working space. The method provides a theoretical basis for the design of the manipulator， and lays the foundation for the task operation planning of the manipulator.

Key words：manipulator， relative manipulability map， inverse kinematics

机械臂是模仿人体手臂而设计的一种自动化操作装置，其运动灵活性反映了对任务操作的转换能力，灵活性指标对于机械臂的设计、评价与运动规划有非常重要的作用，机械臂运动灵活性是机器人运动学研究的一个重要内容。

可操作度、条件数和最小奇异值是比较经典的三个灵活性指标[1]，其中可操作度应用较为广泛，其物理意义可以解释为机械臂各运动方向上能力的综合度量。Yoshikawa将雅可比矩阵与其转置矩阵乘积的行列式的之值定义为机械臂的可操作性指标，并提出了可操作度椭球的概念对机械臂的灵活性进行描述[2]；姚建初等利用方向可操作度对冗余度机械臂进行运动规划，提高了机械臂的运动能力[3]；Hammond等利用加权各向同性指标，对机械臂进行优化设计，并提出了力矩加权各向同性指标，同时考虑了运动灵活性与关节力矩[4]；谢碧云等提出基于条件约束的方向可操作度指标，通过优化侧重点的改变，最大限度地保留了方向可操作度[5]；赵京等采用相对可操作度指标对构型不同的机械臂灵活性分析，筛选出最佳串联仿人机械臂构型[6]。以上对于机械臂灵活性的研究大多针对机械臂工作空间任意点的运动能力进行评价，而对机械臂整个工作空间的灵活性分布情况未进行研究。

本文针对国内外研究的上述不足之处，以机械臂可操作度为基础，建立全局相对可操作度指标，通过对机械臂的位姿离散的方法，结合机械臂逆运动学，基于Matlab平台绘制机械臂全局相对可操作度图，进而从宏观角度出发对机械臂的整个工作空间的灵活性加以分析。本文以Puma560机械臂为示例，研究机械臂工作空间相对可操作度图的构建过程。

1运动学与可操作度

11运动学分析

Puma560是机械臂研究中的典型，由6个旋转关节组成，本体如图1所示。利用D-H法对机械臂建模已成为机械臂运动学研究的标准方法，图2为采用该方法建立的Puma560机械臂坐标系，表1为其DH参数。对于其正逆运动学的求解…[7]，在此不再赘述。借助于机器人工具箱，可以完成Puma560的正运动学解算，并可以得到8组逆运动学封闭逆解。

|det[J（q）]|；机械臂处于奇异形位时，w=0。很容易地可以看到：机械臂除了位于奇异形位时，可操作度指标总是大于零的。此度量指标可以用来衡量机械臂距离奇异形位的远近程度，可以用来衡量机械臂的灵活性。在评价机械臂灵活性过程中，总是希望得到统一量纲指标，为此定义机械臂工作空间的全局相对可操作度指标来对机械臂的可操作性度量指标进行归一化处理[6]，如式（2）所示。

μi=wiwmaxi=1， 2，…，n （2）

式中：wi为机械臂工作空间点pi处的可操作度值，wmax为机械臂工作空间中的可操作度的最大值，μi为上述两者间的比值，称为全局相对可操作度值。当μi=0时，表示该点处于奇异形位；当μi=1时表明该点操作度达到最大值，灵活性最好，显然μi的取值范围是[0，1]。对于Puma560机械臂，在已知各关节角度情况下，采用机器人工具箱可以完成可操作度的计算，本文采用蒙特卡罗方法，完成对Puma560机械臂工作空间的最大可操作度值wmax的求取，再通过式（2）可以得到该形位下机械臂的相对可操作度。

2相对可操作度图构建

21工作空间离散

以两倍的机械臂长度lws为边长，建立一立方体，显然此立方体将机械臂工作空间包含于其中；对该立方体进行网格化处理，将每条边分成长度为lc的nc份，如式（3）所示，如此便把大立方体分成了n3c个小立方体，其边长lclws，工作空间离散化网格划分如图3所示。

机械臂工作空间中任一点都可以划分到各小立方体中，通过式（4）可以计算出所属的小立方体，其中（tx，ty，tz）为机械臂工作空间中的任意点；反之，通过式（5）可以计算出任一小立方体的中心坐标位于机械臂基坐标系下的坐标。采用此种离散方法，机械臂工作空间中的任意位置都可以进行定向分析，每个小立方体22姿态离散

为了将机械臂工作空间任意位置上的姿态进行离散，首先将上述离散空间中的小立方体用与其各面都相切的球体代替，可见当小立方体的边长趋于无穷小时，该球体与小立方体完全一致。采用螺旋点均布算法[8]，在球体表面均匀分布np个小球体，如图5所示，每个小球体的坐标以球坐标的形式给出，如式（6）～（9）所示。

θk=arccos hk，hk=-1+2（k-1）N-1，

1≤k≤N （6）

k=（k-1+36N11-h2k ）（mod 2π），

2≤k≤N-1，1=N=0（7）

xk=lc2·sin θk·cos k

yk=lc2·sin θk·sin k

zk=lc2·cos θk （8）

pi=[xkykzk]T （9）

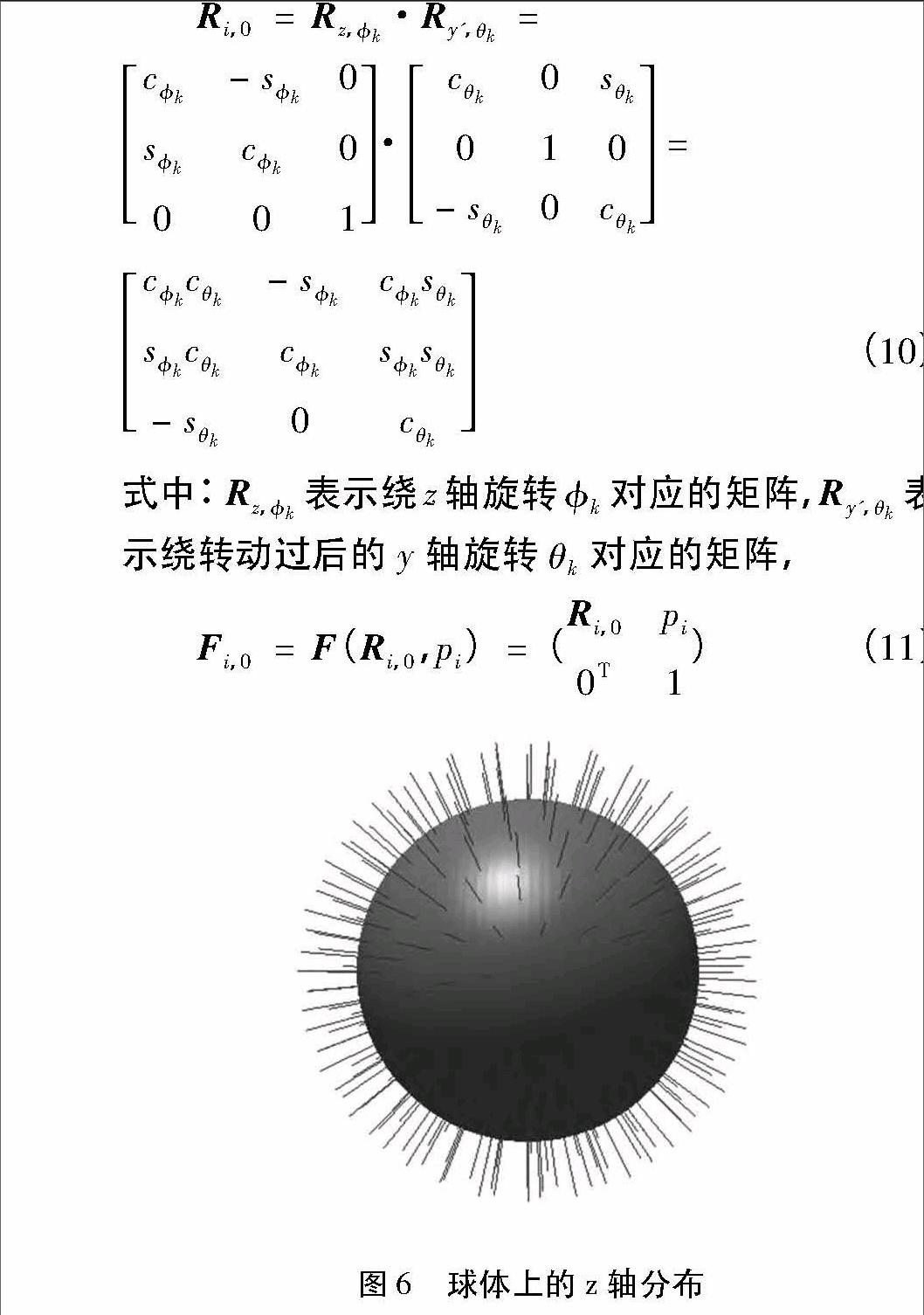
假设大球体和均布的小球体球心都固接有坐标系，大球体坐标系各轴方向与基坐标系一致，小球体坐标系的z轴为由大球体球心与小球体球心的连线，并且指向为大球体球心到小球体球心，通过式（10）与（11）可以得到小球体坐标系到大球体坐标系的变换矩阵，均布小球体的坐标系z轴如图6所示。

至此，可以把Fi，0看作为机械臂的工具坐标系位于大球体下的位姿，而Ri，0就是机械臂的某一姿态。

为了进行姿态离散，将小球体上的坐标系绕其z轴每隔Δ°0旋转一次进行离散，共分成m0份，如式（12）所示，旋转矩阵如式（13）所示，则当小球体上的坐标系旋转过α°k后，其位于大球体下的坐标如式（14）所示。至此，可以将小球体上的任一坐标系位于基坐标系下的坐标通过式（15）和（16）得到，从而完成了机械臂工作空间的任意位姿的离散。

m0=360Δ0（12）

Fz（αk）=Rz（αk）0

0T1αk=k·Δ0k≤m0 （13）

Fi，αk=Fi，0·Fz（αk）=F（Rot（i，k），pi） （14）

TBaseSphere （g）=F（I，w（g））=Iw（g）

0T1 （15）

FBaseTCP=TBaseSphere （g）·Fi，αk=F（I，w（g））·Fi，0·Fz（αk） （16）

23可操作度图构建

通过以上步骤可以实现机械臂工作空间的任意位置和姿态，然而机械臂各关节由于机械结构的限制并非所有的姿态都能到达，Puma560机械臂各关节角度旋转范围如表1所示。因此，在完成机械臂工作空间的位姿离散后，要将每一个位姿进行逆运动学验证，已验证该位姿是否存在逆解。若逆解存在则计算该构形下的相对可操作度，否则按顺序选取下一组位姿值进行计算，重复上述步骤，直至机械臂工作空间所有位姿选尽，程序流程如图7所示。

24Puma560相对可操作度图及分析

按照图7所述机械臂工作空间相对可操作度图构建流程，以Matlab为平台，结合机器人工具箱，进行Puma560机械臂的全局相对可操作度图构建。当Puma560关节取（0，0，-π2，0，0，0）时，机械臂伸直，为所能到达的最长距离，所以大正方体的边长取此时度的2倍为17272 mm，小正方体边长取35 mm，大球体上小球的数量取11，姿态按绕z轴每隔80°取。

为Puma560的全局相对可操作度图，从图中可以看出该机械臂的最大可达空间为一球面，而由于关节机械结构的限制，该球体并不完整，主要表现在从外到内在机械臂第一关节为极限位置时有一个断裂带，并且该球体为中空的。理论上分析，可操作度图球体表面应全为红色即相对可操作度为0，即机械臂处于奇异，而由于位置离散时小正方体的边长取值相对较大，因此球体边缘部分点可操作度较小，但并非为零。为了便于观察机械臂相对可操作度的分布情况，对上述全局相对可操作度图的球体进行剖视，如图9所示。通过图9可以看出，Puma560工作空间的全局相对可操作度大体成带状分布，且大部分空间的相对可操作值达08～10。位于可操作度图球体边缘的点操作度较小，当向球体中心移动时，相对可操作度值变大，然后再变小。图8Puma560工作空间相对可操作度图

3结论

本文从机械臂的工作空间出发，以相对可操作度为基础，通过将机械臂工作空间位置离散与姿态散的方法，完成对机械臂整个工作空间的位姿离散，对位姿离散的方法进行了详细论述，而后以逆运动学为基准，对离散的位姿进行筛选，对于满足逆运动学的位姿进行计算全局可操作度，采用三维直观图对机械臂工作空间的相对可操作度分布情况进行描述，通过图谱可以直观地看出机械臂工作空间内其相对可操作度的分布情况。

参考文献：

[1]熊有伦， 唐立辛， 丁汉，等.机器人技术基础[M].武汉： 华中科技大学出版社， 2013：5-200.

[2]YOSHIKAWA T. Manipulability of robotic mechanisms[J]. International Journal of Robotics Research， 1985， 4（2）：3-9.

[3]姚建初，丁希仑， 战强. 冗余度机器人基于任务的方向可操作度研究[J]. 机器人， 2000， 22（6）：501-505.

[4]HAMMOND Ⅲ F L， SHIMADA K. Morphological design optimization of kinematically redundant manipulators using weighted isotropy measures[C]// International conference on robotics and automation. Kobe Japan， 2009， 2 931-2 938.

[5]谢碧云， 赵京. 基于条件数约束的方向可操作度[J]. 机械工程学报， 2010， 46（23）：8-15.

[6]赵京， 宋春雨， 杜滨. 基于人体工程学的仿人机械臂构型[J]. 机械工程学报， 2013， 49（11）：16-21.

[7]付京逊， R. C. 冈萨雷斯. 机器人学[M]. 北京： 中国科学技术出版社， 1989：8-100.

[8]E B SAFF， A B KUIJLAARS. Distributing many points on a sphere[J]. Mathematical intelligencer， 1997， 19（1）：5-11.