对教材中“空间中点、直线和平面的向量表示”的深度理解

摘 要：从教材对“空间中点、直线和平面的向量表示”的论述出发，在基于数学本质理解概念的基础上，从研究一个数学对象的一般观念入手，结合数学概念生成的合理性，实现对教材的深度理解. 厘清了此内容知识和思维的逻辑，达成“何由以知其所以然”的教材理解．

关键词：向量；几何对象；向量表示

中图分类号：G633.6 文献标识码：A 文章编号：1673-8284（2024）05-0036-03

引用格式：王凯，王红权. 对教材中“空间中点、直线和平面的向量表示”的深度理解［J］. 中国数学教育（高中版），2024（5）：36-38.

人教A版《普通高中教科书·数学》选择性必修第一册（以下统称“教材”）第一章“空间向量与立体几何”第四节第1课时的教学内容为“空间中点、直线和平面的向量表示”，学生通过之前的学习已经建构了空间向量的一些基本概念，从本节课开始会用向量方法刻画立体几何的研究对象. 点、直线和平面是组成立体图形的基本要素，需要先用向量表示这些对象，然后才能在此基础上用向量方法研究立体图形的性质. 本节课内容比较抽象，尤其是对空间中的点、直线和平面的向量表示缺乏深刻理解，大多数教师只能照本宣科.

一、如何用向量表示空间中的一个点

教材中提出的第一个思考是：如何用向量表示空间中的一个点？

点是空间位置的抽象，如果没有参考位置（如坐标原点），点的位置无法用数学方法进行刻画. 物理学中有一个基本假设：没有绝对的位置，即确定一个位置通常需要使用参照物或参考系. 因此，某个点的位置就是以另一个点的位置为参照物的相对位置. 例如，相对于点A，可以指出点P的位置在何处，但如果没有点A，点P的位置就不容易刻画.

在一维空间中，可以这样理解：在直线l上，相对于点A的坐标，点[P]也会有一个坐标. 这个坐标包含两方面信息：一个是方向（表示点P在点A的左侧还是右侧）；另一个是距离（线段[PA]的长度）. 如果规定点A为原点，则点P的坐标为λe，其中e为直线l的单位方向向量，[λ=PA].

显然，坐标原点的选取决定了点P的坐标，但无论是相对于点A还是相对于点B，点P的位置是始终是不变的. 这种不变性就说明了任何一个参照系的选择都是等价的. 因此，可以在空间任取一点O作为坐标原点，那么空间中任意一点P的位置就可以用向量[OP]来表示，把向量[OP]称为点P的位置向量，如图1所示.

【评析】用向量表示空间中的一个点，需要选择一个基点O，则点P的位置就与位置向量[OP]一一对应. 在教学过程中，教师要让学生建立基底意识，为接下来用向量表示空间中的直线和平面积累经验.

二、如何用向量表示空间中的一条直线

教材中提出的第二个思考是：空间中给定一个点A和一个方向就能唯一确定一条直线l. 如何用向量表示直线l？

在平面上，一个点A和一个方向向量a决定了一条直线，用向量来表示这条直线就是要用点A和方向向量a来表示直线上的任意一点.

如图2，如何判断点P在直线l上呢？由共线向量的条件可知，点P在直线l上的充要条件是存在实数t，使得[AP]= ta，即[AP]=[tAB]. 事实上，我们可以在空间任取一点O（如图3），同样可以得到点P在直线l上的充要条件是存在实数t，使得[OP=OA]+ ta，或者[OP=OA]+[tAB]，这都是空间中直线l的向量表示式. 可见，在空间中，同样可以用一个点P和一个方向向量a来刻画一条直线.

这与前面讲“点”一样，无论是相对于哪个基点（原点）O，直线l的位置始终不变. 此时[AB=OB-OA]，向量[AB]不会随着基点O的变化而变化，所以用[OB-][OA]来表示[AB]，与基点[O]的选取无关. 如果[AP=][tAB]，进一步可以得到[OP=1-tOA+tOB]. 这说明向量与坐标原点的选取没有关系，它可以精准地刻画直线的方程.

用向量刻画点和直线与坐标原点的选取无关，就不存在把“确定坐标原点的两个量”（角度和距离）带入运算中. 因此，向量表达简洁，向量运算也比较简便. 事实上，我们就是在用数学的语言刻画直线是“直”的.

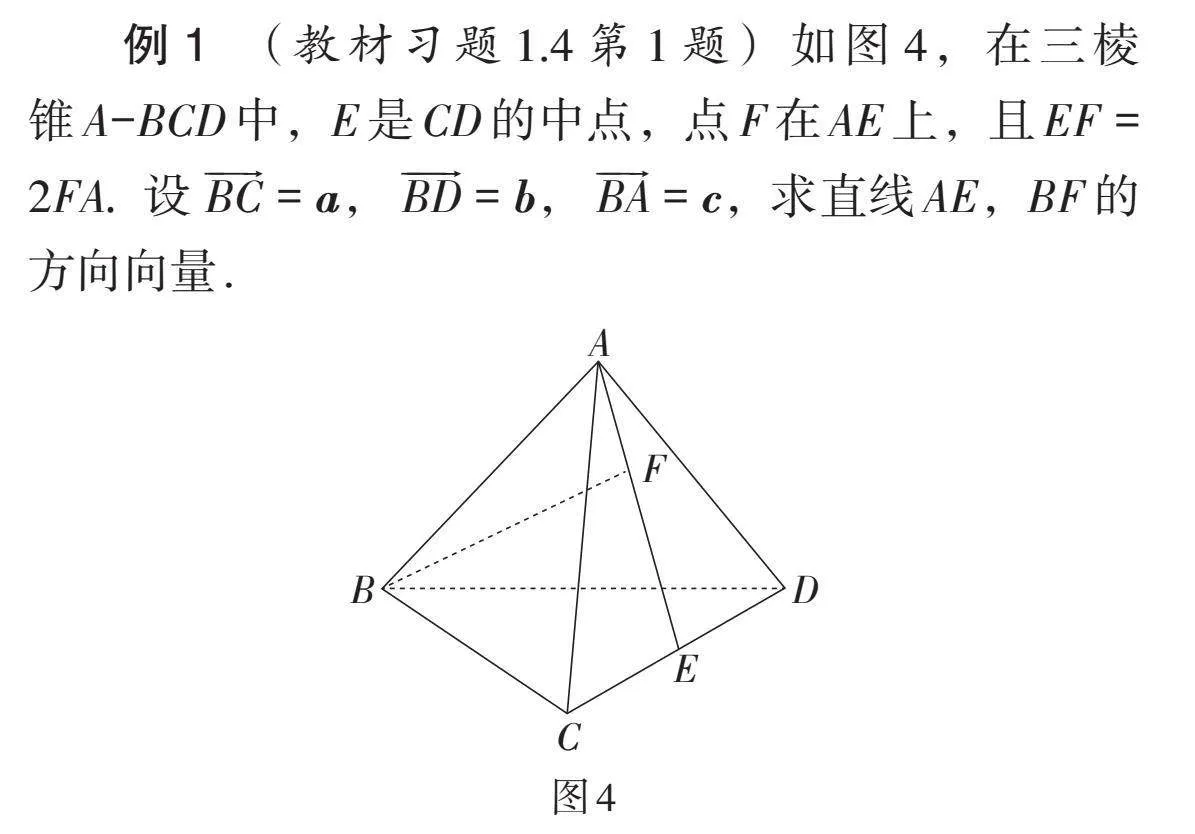
例1 （教材习题1.4第1题）如图4，在三棱锥A-BCD中，E是CD的中点，点F在AE上，且EF = 2FA. 设[BC]= a，[BD]= b，[BA]= c，求直线AE，BF的方向向量.

【评析】让学生体验用空间向量表示直线，将理论应用于实践，提升学生对基底的认识，培养学生对合适的“基底”的敏感和直觉，帮助学生体会向量法在解决问题中所起的工具性作用.

三、如何用向量表示空间中的一个平面

教材中提出的第三个思考是：一个定点和两个定方向能否确定一个平面？进一步地，一个定点和一个定方向能否确定一个平面？如果能确定，如何用向量表示这个平面？

如图5，可以用两条直线来表示平面，即用直线作为基本量，确定一个平面的是两条相交直线. 记两条相交直线的公共点为O，两条直线的方向向量分别为a和b，点O和两个方向向量即可用来描述一个平面. 接下来，寻找空间中的另外一点P，让[OP]在这两条直线构成的平面上，即[OP]= xa + yb. 这里我们用要素（点和直线）表示了平面，说明了平面的“平”. 如图6，与表示直线一样，可以取定空间中任意一点O为基点，得到[OP]=[1-x-y][OA]+[xOB]+[yOC].

【评析】将教材中确定平面的推论转化为向量表示，进一步加深对平面向量基本定理的理解. 让学生在解决具体问题的过程中，再次体会需要根据问题的条件选择合适的“基”，遵循数学学习的一般套路，积累学习经验，提升学习能力.

如图7，还可以用一点A和一个法方向a来确定一个平面α，用集合[Pa · AP=0]来表示. 这样的表示能把点、直线和平面三者串联起来，体现三者之间的内在逻辑关联，使学生对点、直线和平面空间向量表示的理解更加深刻，体现“用数学的语言表达现实世界”的课程标准目标.

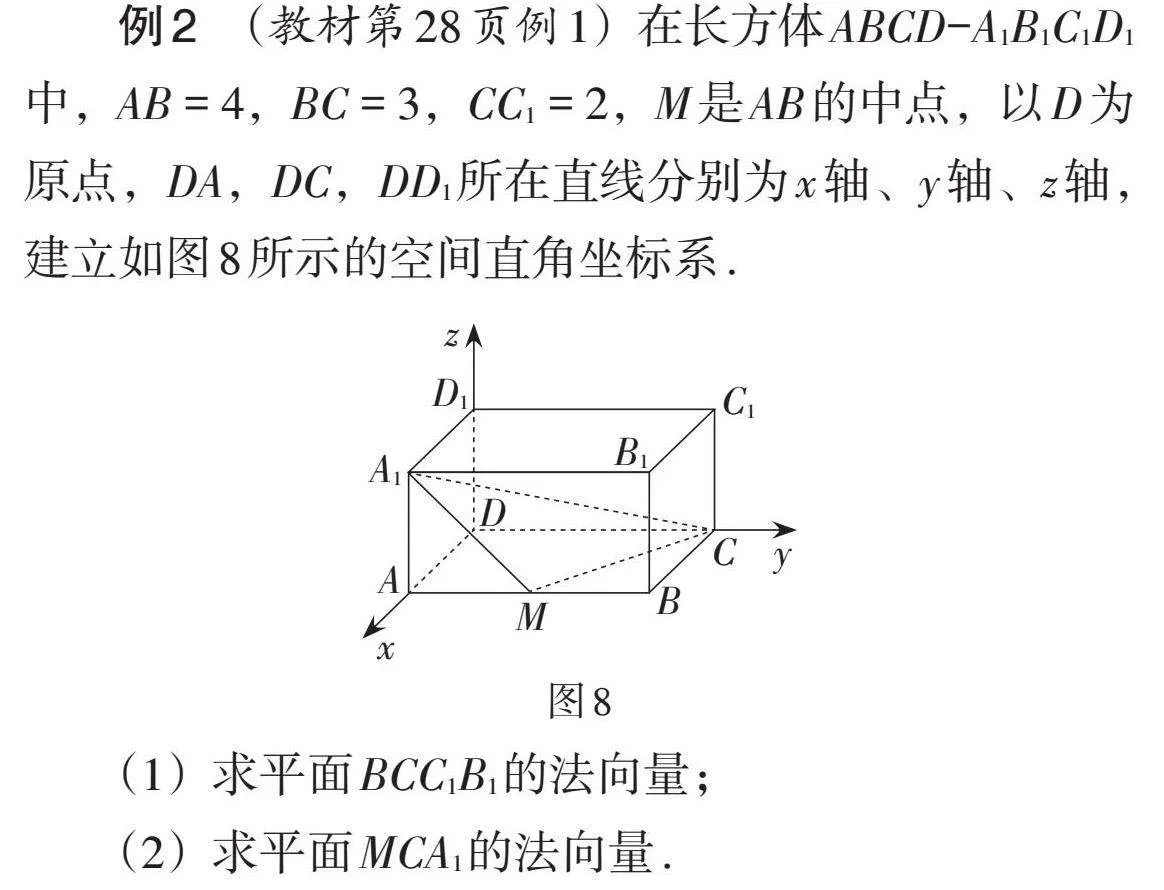
例2 （教材第28页例1）在长方体ABCD-A1B1C1D1中，AB = 4，BC = 3，CC1 = 2，M是AB的中点，以D为原点，DA，DC，DD1所在直线分别为x轴、y轴、z轴，建立如图8所示的空间直角坐标系.

（1）求平面BCC1B1的法向量；

（2）求平面MCA1的法向量.

通过问题的解决获得求法向量的一般方法和步骤. 第（1）小题可以根据线面垂直的判定定理求解，第（2）小题则可以根据向量的坐标表示联立方程组求解.

【评析】通过典型实例，让学生实践求法向量的方法，体会向量方法在立体几何中的作用，为后续用法向量研究直线和平面之间的平行、垂直关系，以及距离、夹角等度量问题做好准备.

四、结束语

方向是刻画直线、平面位置关系的基本工具，角度是对两个向量方向差的度量. 平行和垂直是立体几何中空间直线和平面位置关系探究的主旋律，研究位置关系常常转化为直线的方向向量、平面的法向量的夹角的大小关系.

空间直线、平面都是由一个点和一个方向向量确定的. 直线由一个点和它的方向向量确定，平面则由一个点和它的法向量确定. 事实上，这就是欧氏几何中“过空间一点能作且只能作一条直线与已知直线平行”和“过空间一点能作且只能作一个平面与已知直线垂直”的代数表示.

用空间向量表示空间中的点、直线和平面，都需要先取定空间中的一点作为基点，再以此为基准，将直线和平面上的定点与直线和平面上的任意一点关联起来，从而得出空间直线和平面的向量表示式. 用向量表示空间中的点、直线和平面是用向量法解决问题的第一步，因此合理表示是关键，必须准确反映立体图形的本质特征. 空间向量的表示不依赖于基点的选择，向量不依赖坐标原点的选取，因此向量法不涉及坐标法的烦琐运算，是解决立体几何中位置关系和度量关系的理想选择.

教材通过空间向量的运算，以“思考”栏目为载体，构建了一条问题链，引导学生层层深入地进行思考，让学生掌握其中蕴含的思想方法，认识向量法所起的关键作用，最终让学生得到思维方法上的训练. 教师应该深入理解教材中构建的问题链，并在此基础上进行教学，把学生的思维活动逐步引向深入，帮助学生在获得“四基”的过程中，逐步提升“四能”，发展数学实践能力和创新意识，促进学生学会学习.

参考文献：

［1］中华人民共和国教育部. 普通高中数学课程标准（2017年版2020年修订）［M］. 北京：人民教育出版社，2020.

［2］史宁中，王尚志.《普通高中数学课程标准（2017年版2020年修订）》解读［M］. 北京：高等教育出版社，2020.

［3］章建跃. 核心素养立意的高中数学课程教材教法研究［M］. 上海：华东师范大学出版社，2021.

［4］章建跃. 章建跃数学教育随想录［M］. 杭州：浙江教育出版社，2017.

［5］史宁中. 数学基本思想18讲［M］. 北京：北京师范大学出版社，2016.

［6］王凯. 基于“两个过程”合理性理念下的探究课设计：以“余弦定理”的教学为例［J］. 中小学数学（高中版），2021（5）：29-31.