理解六侧面：低阶到高阶的思维进阶之路

摘 要：思维能力的提升与知识的迁移紧密相关，而理解是实现知识迁移的前提. 以理解六侧面为依据，从理解概念到理解关系再到理解意义，使学生的思维从低阶不断走向高阶.

关键词：理解六侧面；低阶思维；高阶思维

中图分类号：G633.6 文献标识码：A 文章编号：1673-8284（2024）05-0027-05

引用格式：陈姗姗. 理解六侧面：低阶到高阶的思维进阶之路：以“集合”问题为例［J］. 中国数学教育（高中版），2024（5）：27-31.

基于理解的学习有利于知识的迁移，而思维能力的提升与知识的迁移紧密相关，思维从低阶到高阶的跨越主要受制于知识的迁移程度. 影响迁移能力的是人们对知识的理解程度，而不仅是对事实的记忆或对固定流程的遵循，尝试快速灌输大量内容往往会阻碍学习，阻碍即将产生的迁移. 理解是学习的基石，更是促进知识迁移的条件，死记硬背的知识由于缺乏理解而不能进行意义构建，无法在大脑中进行有效存贮、加工和提取. 如何评估学生的理解程度？格兰特·威金斯和杰伊·麦克泰格在《追求理解的教学设计》一书中提出理解六侧面，详细阐述了理解的多重视角，具体如表1所示.

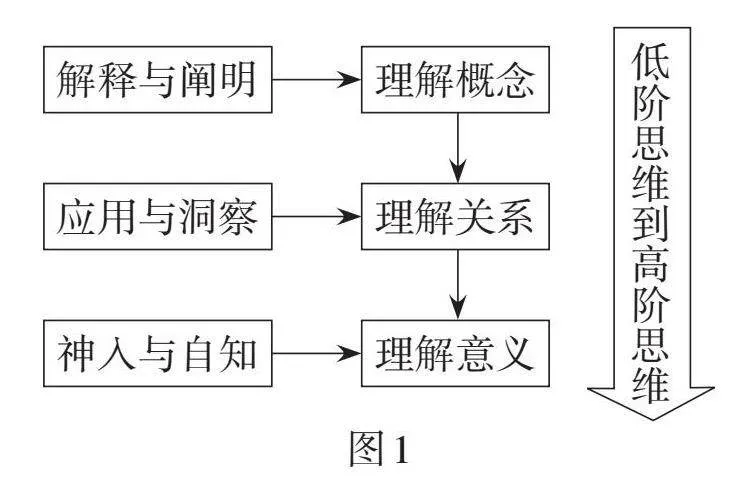
这六个侧面为理解提供了多元化的评估指标. 从更广泛的教育视角来看，这些侧面表明：在促进知识迁移的教学中，理想情况下完整且成熟的理解是指理解六侧面的全面发展. 在理解形成的过程中，通过六侧面从理解概念到理解关系再到理解意义，就是思维从低阶走向高阶的过程，关系如图1所示.

集合是刻画一类事物的语言和工具，属于高中数学的预备知识，其特点是概念多、符号多，抽象程度高. 集合单元内容的学习，可以帮助学生学会使用集合语言简洁、准确地表达数学的研究对象，学会用数学的语言表达和交流，积累数学抽象的经验. 因此，如何帮助学生理解相关概念，理解集合的基本关系、基本运算，以及理解抽象符号的意义是值得研究的问题.

一、解释与阐明：理解概念

李邦河院士认为：“数学根本上是玩概念的，不是玩技巧. 技巧不足道也！”因此，数学教学的重点理应放在理解概念上. 集合部分概念较多，如集合的定义、基本关系（子集、真子集和相等）、基本运算（交集、并集和补集）.《普通高中数学课程标准（2017年版2020年修订）》（以下简称《标准》）中对集合的基本关系和基本运算有着明确的要求. 其中，对基本关系的要求是：理解集合之间包含与相等的含义，能识别给定集合的子集. 对基本运算的要求是：理解两个集合的并集与交集的含义，能求两个集合的并集与交集；理解在给定集合中一个子集的补集的含义，能求给定子集的补集；能使用Venn图表达集合的基本关系与基本运算，体会图形对理解抽象概念的作用. 这些要求中多次提到“理解”一词，这是一个较高的要求，是检验学生习得新知的重要环节. 然而，集合的基本关系与学生熟悉的大小关系不同，集合的基本运算与加减乘除运算也不同，这就给学生理解概念带来了较大的困惑. 因此，教学中教师要采用多元表征对集合的概念进行解释与阐明，以帮助学生理解抽象的概念. 例如，图形表征所具有的直观性特点，使之成为解释抽象概念的一种很不错的方式. 对于集合来说，尤其是对于一些较复杂的集合间的基本运算，仅通过文字表征和符号表征很难理解，可以用Venn图进行解释.

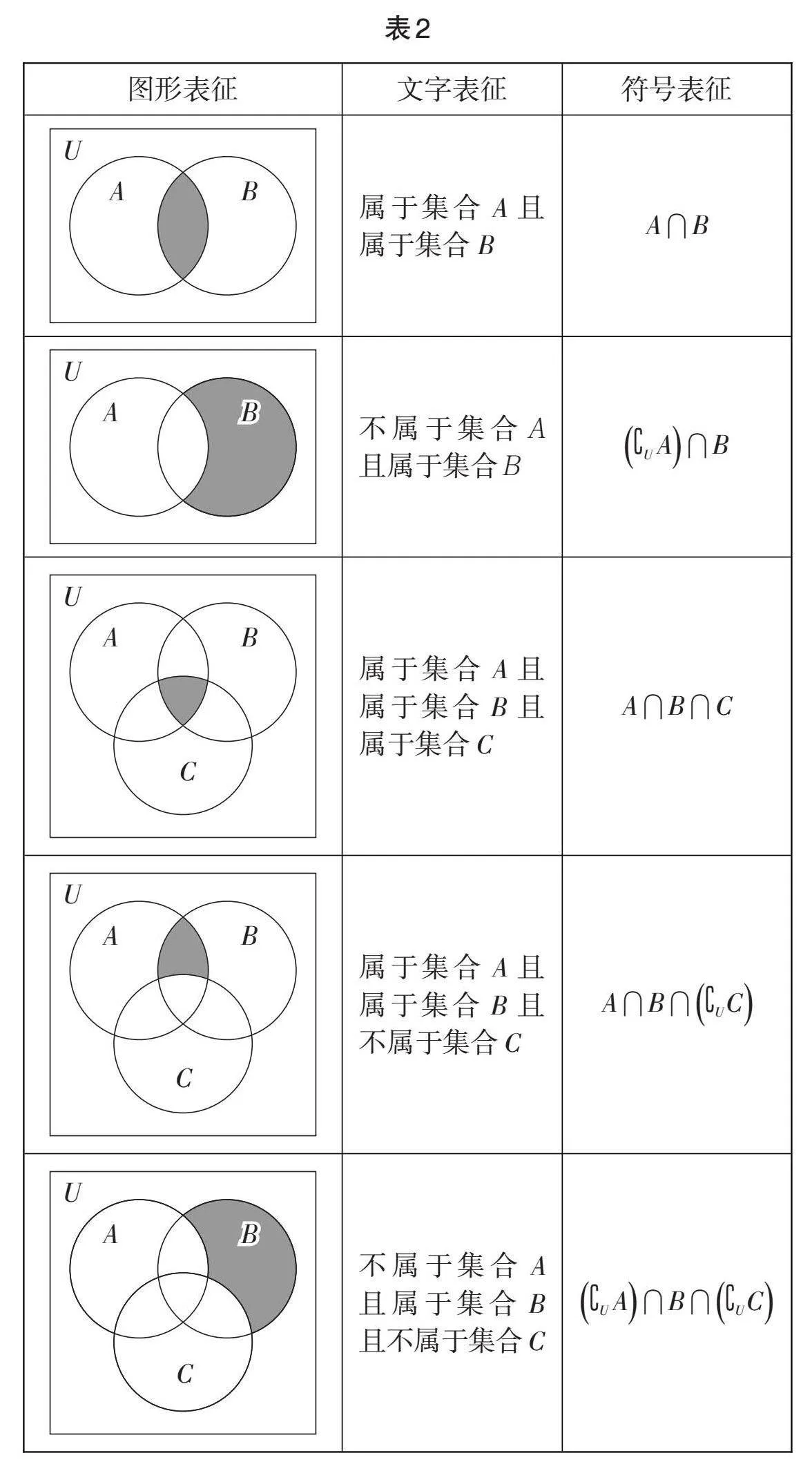
如表2，把集合间的基本运算用不同的表征形式进行解释与阐明，根据VnfD7zjA2uf0ctE6mRSx5pg==enn图中阴影部分表示的元素与集合A，B，C之间的关系，转化为文字语言“属于、不属于”，并用逻辑用语“且”连接，然后把文字表征直接转化为符号表征. 当学生能够将信息从一种表征形式转化为另一种表征形式时，解释就产生了. 解释与阐明集合间的基本运算有助于学生对集合概念的理解，为后续解决集合问题奠定扎实的基础.

二、应用与洞察：理解关系

学习的目的是运用，那些被保存在头脑之中但不能被提取出来加以应用的知识属于惰性知识. 当知识被解释与阐明之后，基于理解六侧面来评估理解的程度，此时思维仅仅被激活而已，还不能称之为深度理解，思维的进一步发展取决于知识能否被灵活应用. 理解六侧面对应用的阐述是“在各种不同的真实情境中有效使用和调整我们学到的知识”. 显然，使用和调整所学知识是应用的关键，在不同情境中应用知识是学生知识迁移能力的体现，《标准》把每种情境分为熟悉的、关联的和综合的. 在熟悉的情境和关联的情境中知识较容易发生迁移，而要想在综合的情境中发生知识迁移，学生必须具有敏锐的洞察能力，感知情境中隐藏的知识背景. 学生对集合基本关系的理解大多数停留在单一的集合之间，而对于较复杂的集合间的基本关系学生很难清晰理解. 对此，可以基于表2对集合间三元交互表征的解释和阐明，引导学生“在先前直接经验的基础上进行敏锐感知”，以理解六侧面中的洞察维度.

例1 全集[U=R，A=x-3≤x<4，B=xy=x+2，]

则图2中阴影部分表示的集合为（ ）.

（A）[xx≤-3] （B）[xx>-3]

（C）[xx≥4] （D）[xx≤4]

例2 已知集合[M=xxx-2<0，N=xx-1<0，]

则下列Venn图中阴影部分可以表示集合[x1≤x<2]的是（ ）.

例3 （多选题）如图3，阴影部分表示的集合是（ ）.

[B][U][A] [B][图3]

（A）[∁UB⋂A] （B）[∁UA⋂B]

（C）[∁UA⋂B] （D）[A⋂∁UA⋂B]

以上3道例题与表2中的情境高度相关，属于相关情境. 对于例1，观察Venn图可知阴影部分的元素由属于[B]而不属于[A]的元素构成，由表2不难确定阴影部分表示的集合为[∁UA⋂B]. 显然，此题的考查重点是学生的识图能力，把图中阴影部分表示的集合用符号表示出来便可以求解. 例2的难度稍微高于例1，要识别四个图形，选项A中Venn图中阴影部分表示[M⋂N]；选项B中Venn图中阴影部分表示[∁UN⋂M]；选项C中Venn图中阴影部分表示[∁UM⋂N]；选项D中Venn图中阴影部分表示[M∪N]. 例3考查集合间的运算，可知阴影部分表示的集合为[∁UB⋂A].

这3道例题均考查对Venn图的识别，要求学生用符号表示出图中阴影部分表示的元素的集合. 如果学生能够理解表2中的5种情况，那么对这3道例题的解答将水到渠成. 随着理解的不断深入，学生的思维也会不断提高.

学习知识的目的是应用，在习得知识的过程中就要考虑应用，做到“以终为始”，这就需要学生在习得知识之后有较强的应用意识和洞察能力.

三、神入与自知：理解意义

“神入与自知”的核心是批判性思维和自我反思，即元认知意识. 侧重从反思的角度对知识进行理解，也就是对知识的复盘，这是思维由低阶走向高阶的转折点. 低阶思维涉及的是“是什么”，而高阶思维更多的是指“为什么”“怎样做”“还能怎样做”. 尤其是面对一些抽象的知识，先要求学生透过现象看本质，这里的“透过”必须建立在“理解意义”的基础上. 布卢姆认知目标金字塔的六个层次从低到高依次为：记忆、理解、应用、分析、评价和‌创造. 其中，理解在记忆之上，学习者需要理解信息的实际含义，能够组织、比较和解释信息. 对意义的理解是深度学习的体现，其表现是能够灵活应用所学知识. 以集合的基本运算和基本关系为例，就是能够在综合的情境中灵活应用并将其熟练转化为多种表征，进而通过不同表征理解数学对象的深刻意义. 以下是集合中常见的三个结论：（1）[A⊆B⇔A⋂B=A⇔A⋃B=B⇔∁UA⊇∁UB]；

（2）[∁UA⋂B=∁UA⋃∁UB]；（3）[∁UA⋃B=∁UA⋂∁UB.]

思维较好的学生可以通过符号表征直接理解，但是处于低阶思维的学生只能死记硬背，这是典型的浅表学习，无法实现知识的意义构建. 由心理学家佩维奥的双重编码理论可知，在信息存贮、加工和提取的过程中，每个人都会使用语言和非语言两个编码系统. 而非语言系统最直观的体现就是可视化，采用可视化的方式能够提高学生意义建构的能力. 因此，可以采用集合知识的典型图示——Venn图，把抽象的表达式可视化、直观化，如图4和图5所示.

通过图4可以很直观地理解结论（1），而对结论（2）和结论（3）的理解则可以通过图5进行区域划分. 降低认知负荷是提高学习效率的一种体现，通过Venn图理解集合的基本运算与基本关系的概念，可以减少记忆的过程. 这种以图式表征的可视化方式对高阶思维进行培养具有重要的价值. 高中数学知识中有较多的常见结论，仅靠死记硬背是不可取的，理解是记忆的基础，只有理解了知识才能实现全面且稳固的记忆.

例4 已知[M，N]均为实数集[R]的子集，且[N⋂∁RM=∅]，则下列结论中正确的是（ ）.

（A）[M⋂∁RN=∅]

（B）[M⋂∁RN=R]

（C）[∁RM⋃∁RN=∁RM]

（D）[∁RM⋂∁RN=∁RM]

认知心理学家认为，学习发生迁移的两个主要因素是学生对知识的理解程度和不同的学习对象之间的相似性. 例4涉及集合的基本关系和基本运算，已知条件“[N⋂∁RM=∅]”较为抽象，学生难以从中看出集合[M]与集合[N]之间的关系，进而就无法对4个选项作出判断. 然而，理解表2的学生已经具备解决这类问题的丰富经验，学习自动发生迁移，即通过Venn图进行解答.

如图6，根据[N⋂∁RM=∅]确定集合[M]和集合[N]的关系时，可以先画出集合[M]. 而集合[N]不能与[M]的补集有交集，所以集合[N]表示的区域只能在集合[M]内或者与[M]重合，即[N⊆M]，如图7所示.

生成图7之后，对4个选项的判断就非常直观了. 学生理解了表2中呈现的集合的基本关系与基本运算之后，就会带着作图的意识进行分析，而不是就题解题.

数学思维是在日常学习中一点一滴地培养起来的，不能一味地追求答案而忽视题目背后的深层意义. 对于一些简单的题目，要以小见大，养成思考的习惯，不仅思考“是什么”，更要思考“为什么”. 在遇到一些新情境的题目时，思维显得尤为重要，除了把抽象的符号表征可视化外，还可以把文字表征转化为图形表征.

例5 我们知道，如果集合[A⊆S]，那么[A]的补集为[∁SA=xx∈S且x∉A]. 类似地，对于集合[A，B]，我们把集合[xx∈A且x∉czMLlWOlVJibJqbImU1aiw==B]叫作集合[A]和[B]的差集，记作[A-B]. 例如，[A=1，2，3，4，5]，[B=4，5，6，7，8]，则有[A-B=1，2，3]，[B-A=][6，7，8]. 下列选项正确的是（ ）.

（A）已知[A=4，5，6，7，8，9]，[B=3，5，6，]

[8，9]，则[B-A=3，7，8]

（B）如果[A-B=∅]，那么[A⊆B]

（C）已知全集[U]，集合[A]，集合[B]的关系如图8所示，则[B-A=A⋂∁UB]

（D）已知[A=xx<-1，或x>3]，[B=x-2≤x<4]，

则[A-B=xx<-2 或 x≤4]

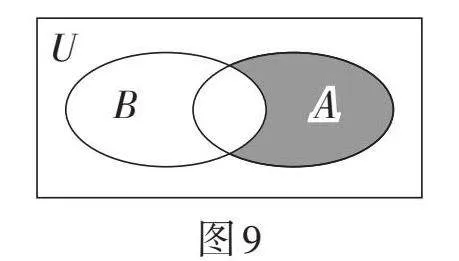
情境是高考试题的考查载体，是问题产生的背景和基础，随着新高考的普及，高考试题更加注重情境化，题型呈现形式丰富多样，无规律可循. 缺乏高阶思维的学生是无法应对的. 此题涉及新定义，如何理解定义是解题的关键. 题干中的新定义与集合的基本运算的定义极为相似，不难想象到用Venn图表示，即先用Venn图表示出新定义，把陌生的问题转化为熟悉的问题. 由[A-B=xx∈A且x∉B]可知，[A-B=]

[xx∈A且x∉B=A⋂∁UB]. 作出的Venn图如图9所示. 通过作图把陌生的情境熟悉化，有利于学生构建解题思路，尤其是对新定义的理解. 在降低学生的畏难情绪的同时，拓宽了学生的解题思路.

理解的形成不是一蹴而就的，而是一个反复的、螺旋上升的过程，从理解概念到理解关系再到理解意义. 在形成理解的过程中，学生将会经历从知识到认知再到迁移的过程，而这个过程需要多侧面的评估，即解释与阐明、应用与洞察、神入与自知. 理解透彻了，思维能力也就提高了.

参考文献：

［1］威金斯，麦克泰格. 追求理解的教学设计（第二版）［M］. 闫寒冰，宋雪莲，赖平，译. 上海：华东师范大学出版社，2017.

［2］中华人民共和国教育部. 普通高中数学课程标准（2017年版2020年修订）［M］. 北京：人民教育出版社，2020.

［3］吴红耘，皮连生. 学与教的心理学（第6版）［M］. 上海：华东师范大学出版社，2020.