指向“归类突破”的微专题课模式研究

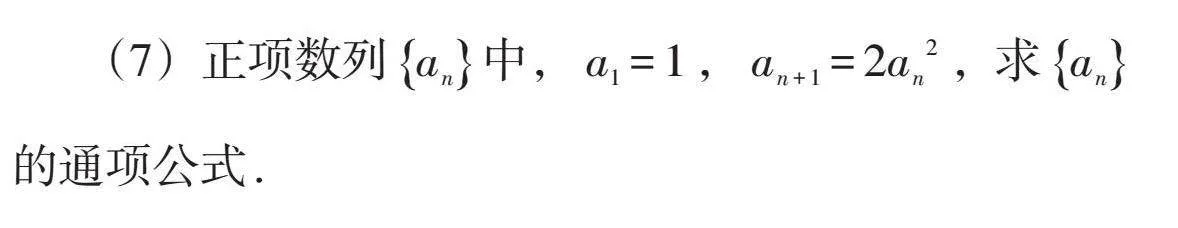
摘 要：根据高中数学微专题课的特点和“归类突破”的原则探究微专题课堂模式的构建，并以“数列的递推关系”为例设计指向“归类突破”的微专题复习.

关键词：归类突破；微专题课模式；数列的递推关系

中图分类号：G633.6 文献标识码：A 文章编号：1673-8284（2024）05-0004-04

引用格式：李现勇，樊星星. 指向“归类突破”的微专题课模式研究：以“数列的递推关系”为例［J］. 中国数学教育（高中版），2024（5）：4-7.

一、引言

微专题是从学生的学情出发，以知识方法为中心串联问题的小切口专题. 微专题课是高三二轮复习的主要形式. 归类教学是高中数学教学的常用教学方法，指在不排除知识积累与适度训练的前提下，更加注重并强调诸多数学问题解决方法上的类别归纳，追溯创设各种情境下的数学问题背后隐藏的通性通法，能对解决办法进行合理的归类并实施有效教学. 归类时应该将具有相似属性、特征或解题方法的知识点或题目归为一类. 同时，考虑知识点或题型的难易程度、深浅层次，按照由浅入深的顺序进行递进式教学. 不仅要关注单个知识点或题型，还要考虑它们与整个数学体系的关系. 归类还可以根据学生的学习情况和教学的需要进行适当调整. 对于一些多角度解决的问题，可以根据不同的解题方法进行多维度归类. 归类的过程和结果应该围绕教学目标进行，如提高解题效率、加深对某一数学概念的理解等，使归类具有目标导向性. 归类的过程应该注重实践性原则，即鼓励学生参与且通过实践活动（如合作探究和小组讨论等）来深化对此类知识的理解和应用.

二、模式建构

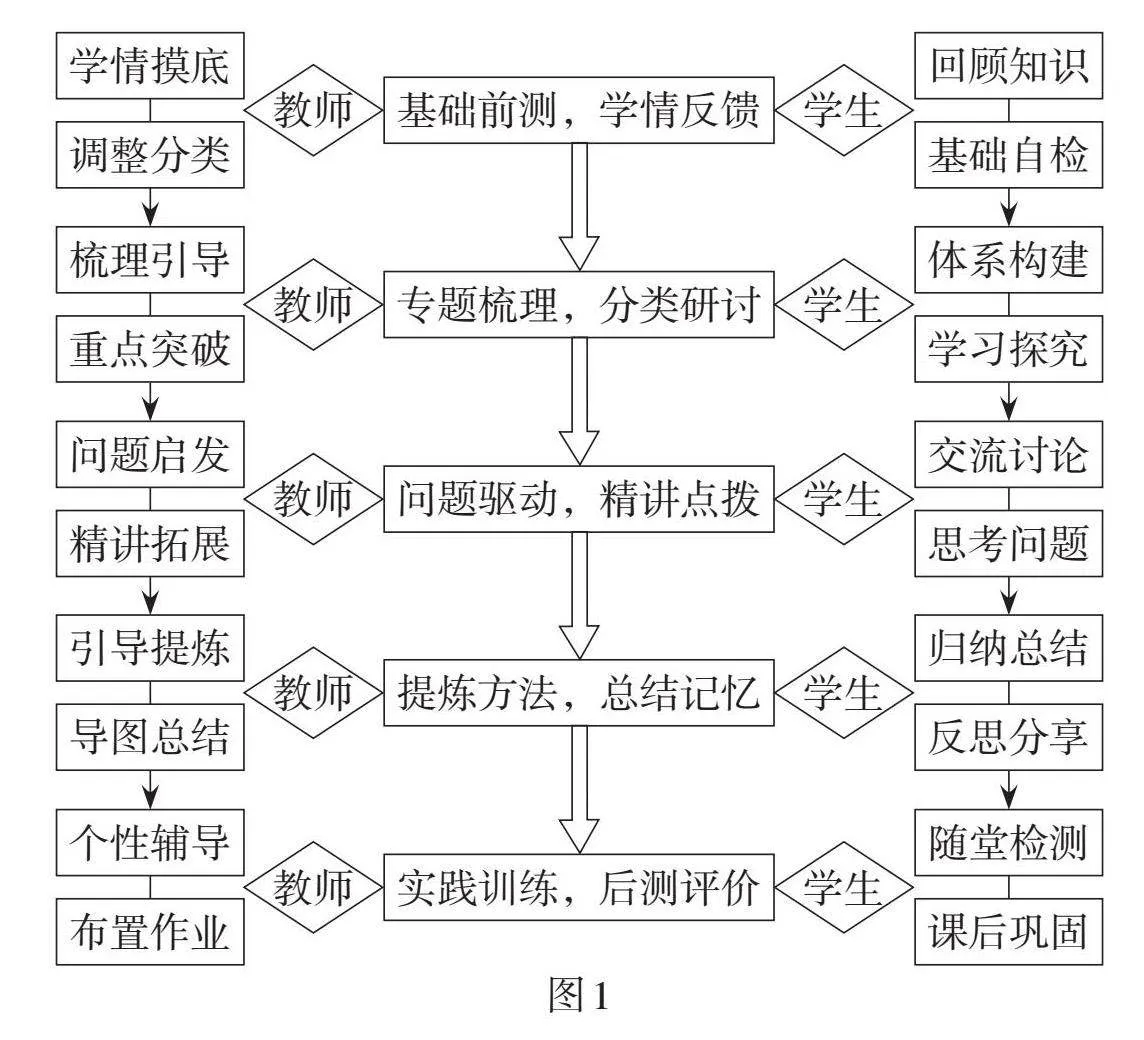
基于以上理论，指向“归类突破”的微专题课的设计必须依据学生的学情、课程标准和高考试题分析来确立微专题的主题和教学的焦点. 将教学内容进行合理分类，精心挑选典型例题和变式题目，并选用适当的练习题进行巩固和反馈. 此外，还需要对教学结构进行周密规划，明确教学内容的排列顺序，设计学生的课堂互动活动，以及确定教学方法和评价策略，最终形成指向“归类突破”的微专题课模式，如图1所示.

三、教学实例

基于上述模式，笔者设计并实施了一堂以“数列的递推关系”为主题的“归类突破”微专题复习课. 此次教学活动是以学生的学习情况反馈为基础，识别学生在掌握数列递推关系方面存在的弱点，并将其作为促进学生能力提升的关键切入点.

1. 基础前测，学情反馈

（1）数列[an]中，[a1=1]，[an+1=an+1nn+1]，求[an]的通项公式.

（2）数列[an]中，[a1=1]，[an+1=n+2nan]，求[an]的通项公式.

（3）数列[an]中，[a1=1]，[an+1=3an+1]，求[an]的通项公式.

（4）数列[an]中，[a1=1]，[an+1=2an+n-1]，求[an]的通项公式.

（5）数列[an]中，[a1=1]，[an+1=2anan+2]，求[an]的通项公式.

（6）数列[an]中，[a1=1]，[an+1-3an=2anan+1]，求[an]的通项公式.

（7）正项数列[an]中，[a1=1]，[an+1=2an2]，求[an]的通项公式.

【设计意图】《普通高中数学课程标准（2017年版2020年修订）》（以下简称《标准》）中对数列通项有具体要求：“能够结合具体实例，理解通项公式对于数列的重要性，知道通项公式是这类函数的解析表达式.”依据“归类突破”的相似性原则，设置数列的递推关系课前基础测试，让学生进行知识回顾和自检，检测学生对此数列递推关系基本题型的掌握程度. 教师通过批阅作业摸清学情，寻找学生的易错点和能力增长点，并根据学情进行微专题教学内容的设置.

在本案例的实际操作过程中，第（4）题学生的错误率最高，主要错误原因是利用同构思想进行构造时形式错误，深究内因是学生对同构思想的理解不够深入，导致应用出错，而同构思想在高中数学的数列、函数与导数、解析几何等知识中均有体现. 因此，基于学情将本微专题教学的重点放在[an+1=2an+n-1]及其变式，教学目标为对同构思想的深入理解和应用.

2. 专题梳理，分类研讨

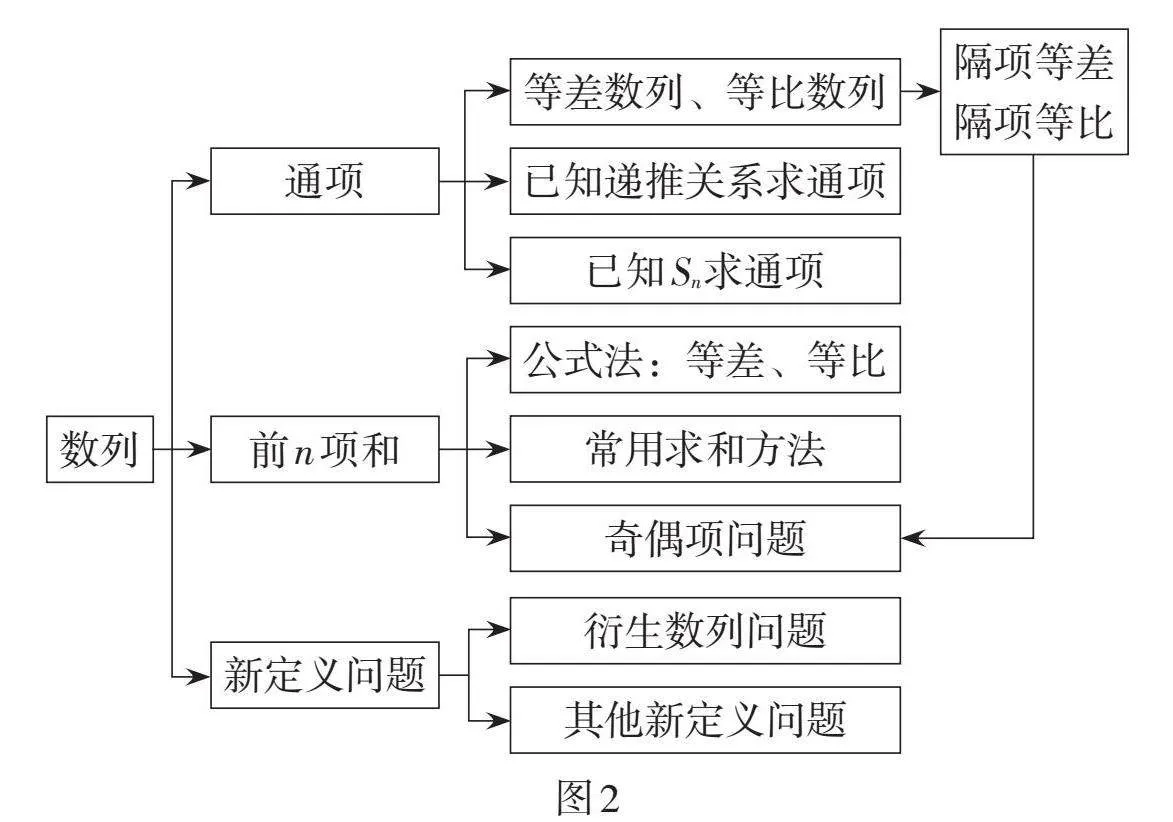
首先，以全局视角呈现“数列”部分大专题的完整结构（如图2），帮助学生建立知识体系，体现了归纳突破的系统性原则. 这种方式旨在为学生提供一个清晰的学习方向，使他们能够更好地理解微专题内容在大专题中的作用，从而在学习过程中形成更为连贯和结构化的认识.

其次，依托细致的学情检测分析，对教学内容展开精细化归类梳理. 对于学生已经深度掌握的部分，通过对应用方法及技巧的系统总结与归纳（如表1），引导学生在复习过程中加深对知识内涵的理解，并挖掘和探求不同知识点之间的内在联系；针对存在疑惑或掌握尚浅的知识点，拟在后续环节采纳归类讨论的方式，对这些内容进行针对性地深化与突破.

3. 问题驱动，精讲点拨

例1 数列[an]中，[a1=1]，[an+1=2an+n-1]，求[an]的通项公式.

问题1：在题目（3）[an+1=3an+1]中，你使用了什么方法求[an]？

问题2：能否用同样的方法求解例1？

问题3：以下做法有何错误？

问题4：这种方法的要点是什么？

【设计意图】题目（3）是学生能够熟练应用同构思想进行构造的题目类型，用学生熟悉的题目类型作为启发点，通过提供正确和错误的同构形式让学生观察、比较、辨析，总结出构造法的要点为同构，同构要求结构相同、变量不同，而数列中变量对应的是数列的下标. 因此，在数列的同构过程中，要注意与数列下标的对应关系.

变式：数列[an]中，[a1=1]，[an+1=2an+4×3n-1]，求[an]的通项公式.

学生活动：分小组研究、讨论此题的特征，并利用同构思想进行构造，讨论时间为3分钟，随后进行小组展示.

【设计意图】在例1的基础上进行变式，以检验学生对同构的理解程度和应用能力. 一些学生习惯使用观察配凑的构造方式解决问题，引导学生学会使用待定系数法进行构造. 同时，通过小组展示构造的不同的同构形式，培养学生对问题进行多角度思考探究的能力，最终将不同类型的问题归类，并总结出相应的解决策略.

例2 数列[an]中，[a1=5]，[a2=2]，[an=2an-1-]

[an-2 n≥3]，求[an]的通项公式.

变式：数列[an]中，[a1=5]，[a2=2]，[an=2an-1+][3an-2 n≥3]，求[an]的通项公式.

问题1：你能用同构思想对上式进行构造吗？构造完成后相互交流，大家构造出来的式子形式相同吗？

问题2：这些形式可以分别用什么方法求通项？

问题3：能否优化一下，降低计算的难度？

【设计意图】通过对由易到难的两个三项递推例题的探究，带领学生寻求三项递推题目的突破方法，考查学生的迁移能力和对同构思想的应用能力. 学生分别构造出[an+an-1=3an-1+an-2]和 [an-3an-1=-an-1-3an-2]

两种形式，教师引导学生多思少算，综合考虑两种形式下所得的[an+an-1]和[an-3an-1]的通项公式，通过加减消元得到数列[an]的通项公式，进一步体现利用待定系数法构造新数列的重要性.

4. 提炼方法，总结记忆

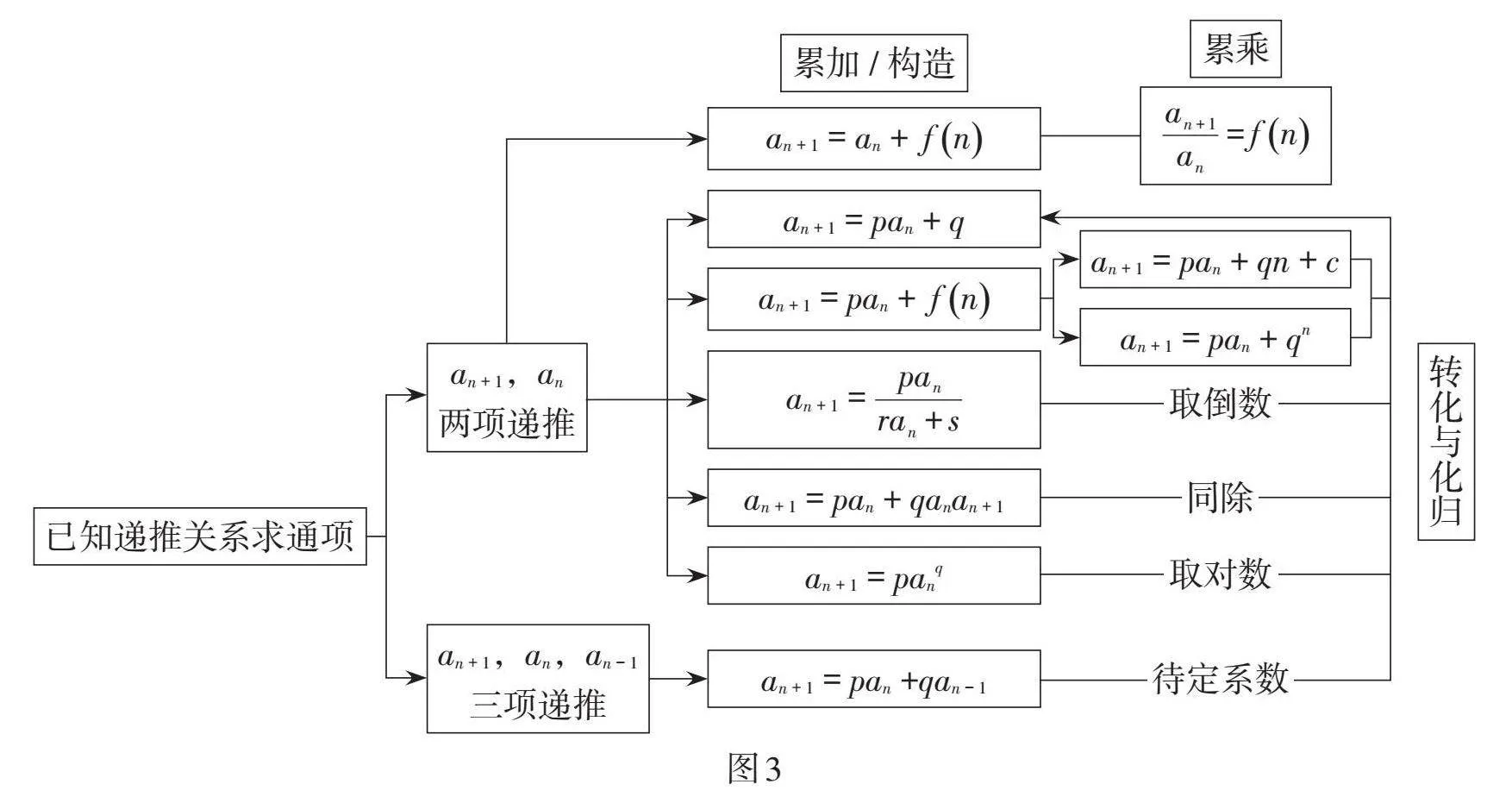
将例1及其变式归类为[an+1=pan+fn]型，将例2及其变式归类为[an+1=pan+qan-1]型，并总结相应的解题方法和思路，最后以思维导图的形式总结该微专题所涉及题型的“归类突破”和思想方法的总结提升，如图3所示.

5. 实践训练，后测评价

（1）在数列[an]中，[a1=3]，[an+1=2an-n+2]，若[an>980]，则[n]的最小值是 .

（2）已知数列[an]满足：[a1=2]，[an+1=an+2n]，则[an]的通项公式为 .

（3）已知数列[an]满足[a1=2]，[a2=6]，且[an+2-][2an+1+an=2]，若[x]表示不超过[x]的最大整数（如[1.6=1]，[-1.6=-2]），求[22a1+32a2+…+2 0242a2 023].

【设计意图】通过实施分层的评估与反馈机制，使学生能够根据自己的学习水平接受适当的挑战和支持，同时强化学生对学习内容的理解和掌握，增强了学生的自信和动力，更有效地识别并挖掘了学生的潜力.

四、反思总结

《标准》提出高中数学课程以学生发展为本，要求启发学生思考，引导学生把握数学内容的本质. 因此，微专题的设计要从实际学情出发，从知识的整合回顾检测入手，找到学生的易错点和能力的增长点，开展针对性的微专题靶向训练，以提高复习的效率. 同时，“归类突破”不能仅存在于微专题课堂中，教师还应该引导学生将“归类突破”的方法应用于平时的错题整理中，分类整合错题并总结经验，提高错题资源的利用效率.

微专题中，归类要符合逻辑，不能罗列堆砌，要注意例题和变式内在变化的规律性，引导学生进行合乎逻辑地总结，强化化归思想的应用. 针对不同程度的学生，可以设置不同难度的题组，从“形似质同”到“形异质同”再到“形似质异”层层递进，以促进个性化教学的实施.

“归类突破”强调运用归纳和演绎的思维方式，帮助学生在归类的基础上总结解题的规律和方法，从而培养学生的逻辑思维能力和解决复杂问题的能力.“归类突破”教学不局限于单一知识点或题型的传授，更注重将知识进行系统整理和联系，以帮助学生建立完整的知识体系，增强学习内容的连贯性. 在“归类突破”的教学过程中，学生不仅要接受知识，还要主动参与分类和归纳的过程，以增强自主学习能力. 这种教学方式能够促进学生形成独立思考的能力，有利于创新人才的培养.

参考文献：

［1］徐国平. 高中数学“归类溯源教学”的实践与探讨［J］. 中学数学研究，2015（10）：1-5.

［2］中华人民共和国教育部. 普通高中数学课程标准（2017年版2020年修订）［M］. 北京：人民教育出版社，2020.