数形结合思想在小学数学教学中的应用策略探究

【摘要】数学结合思想是小学数学教学中的重要思想，也是解决问题时的重要思维，旨在将代数与几何图形直观联系起来，以具体的图形和数字来呈现抽象问题，并引导学生通过对数量关系、空间形式的研究来解决数学问题.数形结合思想的运用能为课堂增添一丝趣味性、生动性，将复杂深奥的问题变得简单化，从而深入理解数学概念和定理知识.文章简述了数学课堂中应用数形结合思想的意义，并多以数解形、以形助数、数形结合、数形互换、图式结合五个维度探究数形结合在小学数学课堂中的应用策略.

【关键词】数形结合；小学数学；应用策略

小学生正处于形象思维阶段，数学又是一门逻辑性较强的学科，一些知识具有抽象性特点，学生在学习中经常会遇到阻碍和困难.而数形结合是帮助学生攻克思维难关的有效“法宝”，合理运用能将抽象的数学关系以直观图形呈现出来.教师在教学过程中应充分利用数形结合思想，拓展学生思维，简化数学解题程序，从而降低数学学习难度.

一、数形结合思想在小学数学课堂教学中的应用意义

（一）降低学生数学学习难度

逻辑性强是数学学科鲜明的特点，很多学生在认识到这一点后产生了畏难心理.众所周知，抽象的数学公式是学生学习数学知识中的难点，复杂的数学问题是学生常遇到的难题，若是在课堂中借助数形结合思想来启发学生思维，将抽象知识转为具体图形，解决学生学习中的一些困难，对问题有更直观、形象的思考，这无疑能帮助学生梳理解题思路，简化解题时的推导过程，从而提高课堂教学效率.

（二）助力学生巧解数学难题

数学是专门研究数量关系和空间形式的学科，在教学中合理运用数形结合思想，能将抽象的数量关系转化为具体的几何图形，激发学生的形象思维，让学生结合已掌握知识分析所见、所学，从而强化学生对新知的认识，对旧知的温习.由此，学生的数学素养逐渐提高，解决问题的能力也越来越强.

（三）利于学生推导数学公式

随着小学生学段的提升，陆续会接触较多的公式、运算规律，若仅凭刻板记忆，解题时无法灵活运用.而教师运用数形结合思想引导学生推导和分析，能让学生直观认识到公式中蕴含的算理，从而深度对数学公式的理解和掌握.此外，由于公式主要由数字、字母和符号组成，利用图形辅助公式推导和理解，能助力学生进一步理解和掌握知识.

二、数形结合思想在小学数学教学中的应用策略

（一）以数解形———数学语言更加生动

新课改以来，小学数学课程形式及开展要求发生了一系列的变化，主要体现在内容编排、教学内容、教学目标等多个方面.当前，小学数学教材中将传统应用题教学融入解决问题中，并要求教师指导学生掌握解题方法，培养解题能力.但实际教学中，部分教师对应用题教学方法讲授不多，认为应用题教学方法有机械、呆板的特点.因此，在解决问题过程中，教师更多引导学生探索解题思路，很少传授解题策略，这样一来，学生的解题自由性增加，思维发散度却不足.为了解决这一问题，教师应在课堂中运用以数解形策略教学，借助数字图像来代替文字语言，让学生分析中获取直观信息，理解题目中表现出的复杂含义.基于此，学生一方面可以通过直观的图形来理解数学知识，另一方面，还能借助图像来思考数学问题，避免解题时出现思维瓶颈.

以人教版小学数学四年级上册“平行四边形和梯形”的教学为例，教师在解题教学中可以引入数形结合思想，让学生结合图形分析问题，降低解题难度的同时巩固课堂所学知识，具体内容如下：

现有高为6厘米的平行四边形和梯形，其中梯形的上底与平行四边形的下底长度相等，均为10厘米，而梯形的下底比上底长3厘米，求这两个图形的面积之差.

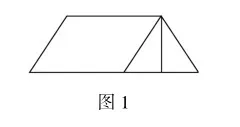
学生在解答这一几何问题时，明确知道需要用到梯形公式和平行四边形公式，但文字中的条件较为复杂，大部分学生都是先结合题目中给出的条件，分别计算出梯形、平行四边形面积，即梯形面积=（10+10+3）×6÷2=69（平方厘米），平行四边形面积=10×6=60（平方厘米），再用梯形面积减平行四边形面积，即69-60=9（平方厘米）.但这对逻辑思维较弱或计算能力不足的学生而言，难度较大，解题时容易受到条件干扰而解题错误.对此，教师应指导学生通过画图的方式来寻找解题思路，实现复杂问题简单化的目的.学生结合题意画出如图1所示的图形，学生可以轻松的发现，平行四边形与梯形的面积之差，是一个三角形，只要求出三角形的面积，就可以得到问题答案.由此，学生观察图形发现三角形的底边长度为3厘米，高与梯形、平行四边形相等，为6厘米，三角形面积=6×3÷2=9平方厘米.基于此，这种解题方式更简单、更便捷，学生计算时思路也更加清晰，降低学生学习难度的同时提升思维能力.

（二）以形助数———明确数量关系

《义务教育数学课程标准“2022年版”》中提出了培养学生解决问题能力的重要性，认为教师在注重解题策略的指导，让学生在面对实际问题时，能运用所学知识从多个角度去思考解决问题的策略.对此，教师可以采取“以形助数”的方式，利用图形来表示数量关系，让学生将题目中复杂的数量关系转化为直观的图形，从而对其中蕴含的数量关系有更深刻的认识.

以人教版小学数学三年级上册“倍的认识”教学为例，为了让学生掌握“倍”的概念，明确“谁是谁的几倍”问题，教师应借助图形来指导学生分析数量关系.首先，教师提出数学问题“周五放学后，学校进行大扫除，某班级12人在擦拭桌椅，4人在扫地，问擦拭桌椅的人数是扫地人数的多少倍？”学生结合所掌握知识展开分析，可以列出式子为：12÷4=（3）倍.但其中部分学生并未完全理解题意，对其中的数量关系也是一知半解，只是利用经验列式解题而已.对此，后续教学中，教师要进一步引导学生思维.随后，教师继续设问“周末，小明要去文具店买一副军棋和一副象棋，已知军棋的价格是8元，象棋的价格是军棋的4倍，请问象棋的价格是多少？”教师给予学生思考时间列式解答，发现部分学生混淆了“倍”的概念，列出的式子为：8÷4=2（元）.教师要结合学生出现的错误启发其思维，先鼓励学生思考题目中等量关系是什么，学生思考后认为等量关系是军棋的价格×4=象棋的价格.最后，教师指导学生用“线段图”来分别表示军棋、象棋的价格，先用1条线段来表示军棋的价格，再用相同长度的4条线段来表示象棋的价格，明确象棋与军棋之间的倍数关系，从而认识到题目的本质是求4个8是多少.基于此，学生懂得利用图形来概括题意，提炼出题目中蕴含的数量关系，进而找到解决问题的正确思路.

（三）数形结合———养成严谨思维

理解题意是学生解决数学问题的关键，但在实际教学中，很多学生存在题意理解不清的情况，多是利用题目中的条件和数据，生搬硬套，解题过程出错的概率自然较高.对此，教师应指导学生掌握题目中的数量关系，把握这一主线后再发散思维，解题难度则大大降低.具体来说，教师可以运用数形结合思想，引导学生将题目中的关键信息转化为图形，再从条件出发去思考，画出线段图或思维导图，让数量关系更加形象，进而结合其中的数量关系逐步列出算式解决问题.

以人教版小学数学四年级下册“数学广角———鸡兔同笼”教学为例，鸡兔同笼问题是学生小学数学学习中的一大难点，对学生的思维能力、想象能力和推理能力有较高的要求，教师可以借助数形结合的方式来锻炼学生的数学思维.首先，教师为学生设计鸡兔同笼问题，如“小明的妈妈在家养了鸡和兔子，共有13只，这些鸡和兔子共有36只脚，那么鸡和兔子各有几只？”这类问题的解决过程对学生而言很麻烦，若教师引导学生利用画图法来分析其中的数量关系，学生则更容易理解题意，且找到解决问题的方法.其次，部分学生的画图能力较差，教师应给予学生有效的指导，在学生画图的过程中，教师可以鼓励学生用圆形来表示鸡和兔子的头，共画出13个圆形，再引导学生思考鸡与兔子的脚有什么区别，学生结合生活经验认识到鸡有2只脚，而兔子有4只脚.而后，教师指导学生为每个头先添上2只脚，数一数后发现只画出了26只脚，再将剩下的10只脚填在图画中.这样一来，学生根据图画内容可以明确认识到，小明妈妈养了8只鸡，5只兔子.最后，教师引导学生回顾画图的流程，说一说为什么要这样画，每一步代表什么含义.学生结合画图步骤，认识到13个圆形代表鸡和兔子的总数量，先在每个头下添2只脚，是假设养了13只鸡，而13只鸡有26只脚，已知条件是鸡和兔子共有36只脚，可见多余的10只脚是兔子的脚，又因为兔子比鸡多2只脚，所以10÷2=5（只），从而得出正确答案.

（四）数形互换———发散数学思维

所谓“数形互换”指的是数字、图形之间灵活转换.随着学段的提升，学生在解题时经常会遇到综合性数学问题，这类题目中往往具有复杂的逻辑或繁多的条件，解题时需要多次转换“数”与“形”的关系，否则将无法完整呈现解题过程.而小学生受到思维能力和解题经验的限制，刚开始接触这类数学问题时感到吃力，不仅会影响解题效率，还会降低对数学学科的积极性.因此，小学数学教师应在保证教学目标的前提下，探索如何降低学生的学习难度.数形结合思想的运用，能有效启发学生思维，数形之间的转换能提高学生解决数学问题的能力，使学生在阅读、分析和解决问题的过程中，养成运用文字、图像的好习惯.

以人教版小学数学四年级下册“运算定律”教学为例，教师在讲解乘法分配律时，若直接分析公式的组成和推导过程，学生理解有一定的难度，对此，教师可以利用图形来代替数学语言.首先，教师利用多媒体展示乘法分配律的公式，a（b+c）=ab+ac，要求学生通过画图来表示这一公式，并组织语言解释定律，部分学生选择利用长方形周长来解释这一公式，并赋予公式中字母新的含义.这一过程中，学生不仅可以加深对公式理解，更能通过分析图形和符号，对这一公式产生认同感.随后，教师鼓励学生以小组为单位，利用长方形周长公式来解释乘法分配律，在讨论中呈现思维推导过程，并其他倾听小组成员的想法和意见，用以完善自身的解题思维.最后，教师围绕乘法分配律设计应用题，要求学生从题目的角度出发，用图来代替题目中的数学语言，再列式解答问题，完成对乘法分配律意义的深入了解.

（五）图式结合———丰富解题策略

图式结合的方式能启发学生多维度探究解题思路，是培养学生解题思维，提高解题能力的重要举措.图式结合，顾名思义就是利用图形和公式来分析数量之间的关系，即先结合题意画出图形，再参考题目中的数据，提炼出题目中的数量关系，指导学生借助问题多维度展开思考，从而找到正确的解题思路.同时，根据小学数学知识体系结构，图式结合方法的运用还能激发学生的创造力，丰富学生的解题思路.

以人教版小学数学六年级上册《分数乘法》教学为例，为了让学生了解单位“1”与部分之间的关系，教师应指导学生通过画图来分析题目的数量关系，以提高学生解决问题的能力，具体内容如下：

结 语

总的来说，在小学数学教学中合理运用数形结合思想，通过画图来助力学生理解知识，能在解决问题的同时建立数学模型，使学生真正做到举一反三，掌握运用各种图画来分析和解决问题的技巧.由此，将抽象的数量关系具象化、形象化，能让学生掌握知识的同时感知到数学学科的魅力.

【参考文献】

[1]李晓林.数形结合思想运用于小学数学教学中对策探讨[J].学周刊，2022（29）：30-32.

[2]胡陈.小学数学教学中数形结合思想的应用探析[J].读写算，2022（27）：61-63.

[3]郭红梅.数形结合：小学数学高效教学的法宝[J].学周刊，2022（28）：84-86.

[4]罗伟红.巧用数形结合思想，化解小学数学难题[J].基础教育研究，2022（18）：46-48.

[5]王水娥.浅析小学数学教学应用数形结合的策略[J].学苑教育，2022（27）：34-36.