新课标下小学数学“空间观念”的培养和思考

【教学目标】

1.使学生结合具体的实例，探索并发现平面图形按比例放大后面积的变化规律。进一步加深对图形放大和缩小的含义以及比例意义的理解。

2.使学生经历由特殊到一般的学习过程，进一步积累观察、比较、分析、概括、归纳等活动经验，感悟归纳的思想和方法，发展数学思考。

【教学重点】

引导学生通过观察、比较，自主发现“如果把一个图形按n∶1的比放大，放大后与放大前面积的比是n2∶1”。

【教学难点】

能利用发现的规律解决实际问题。

【教学过程】

一、故事导入，设疑激趣

师：同学们，你们喜欢听故事吗？那么我们就来听一个《阿凡提智斗巴依老爷》的故事。

播放短片：巴依老爷对阿凡提说：“你的土地这么肥沃，来年土地的租金得扩大5倍！”阿凡提沉思片刻，对巴依老爷说：“尊敬的巴依老爷，我答应你，不过土地得按3∶1的比放大。”巴依老爷一听，暗暗得意：“好！好！就这么定了！”

师：到底谁占了便宜呢？谁来和我们说一说。

生1：把土地按照3∶1的比放大，面积会扩大9倍，而巴依老爷只把租金扩大了5倍，显然阿凡提占了便宜。

生2：面积是32∶12=9∶1，阿凡提占了便宜。

……

师：看来，面积比与长度比有着密切的联系。今天这节课，咱们就来研究面积的变化。（板书课题：面积的变化）

（反思：创设《阿凡提智斗巴依老爷》的故事，激发学生学习的积极性，唤醒学生强烈的参与意识。学生调用已有的知识储备和生活经验，能发现故事中暗藏的小秘密，从而为接下来探究图形面积比与长度比之间的关系做铺垫。）

二、探索长方形面积比与长度比的关系

（一）简单入手，感知关系

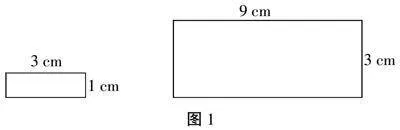
师：数学研究一般从简单入手，我们先来看一看这两个长方形，它们的对应边有什么联系呢？（出示图1）

生1：宽和长的比1∶3。

生2：长和宽都扩大了3倍。

生3：大长方形和小长方形对应边的比是3∶1（板书：对应边的比3∶1），大长方形是小长方形按照3∶1的比放大后得到的。（板书：按比例放大）

师：那它们的面积又有怎样的联系呢？你是怎么想的？

生1：用计算的方法。

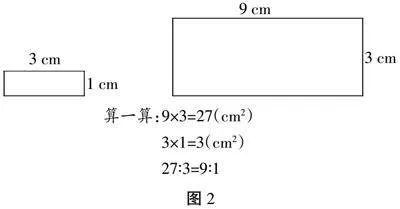
师：那你来算一算。（出示图2）你会用数字说话，真有数学的眼光。谁还有其他的方法吗？

生2：边长扩大3倍，面积扩大3的平方倍。

师：你知道的真多！那到底是为什么呢？今天我们就来一起研究。

生3：画一画：小长方形拼到大长方形中……

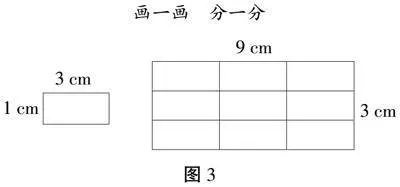
师：我猜你脑海里一定有了这样一幅图，看（出示图3），是不是这样？

画一画 分一分

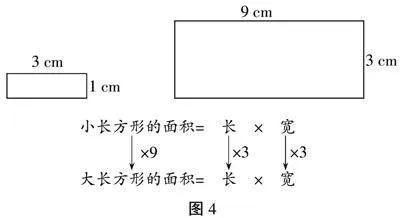
师：除了结合数据、图形，你还能结合长方形的面积公式说一说长和宽分别发生了怎样的变化吗？

生4：长方形的面积=长×宽，因数（长）和因数（宽）都扩大3倍，积（长方形的面积）扩大9倍。9÷3=3 3÷1=3或大长是小长的3倍，大宽是小宽的3倍……长的比3∶1，宽的比3∶1，3×3=9。

师：你能从长方形的面积公式入手，联系以前学的积的变化规律，真会融会贯通！（出示图4）

师总结：结合数据、图形、公式推理我们都发现了当长方形对应边的比是3∶1时（师边指边说），放大后和放大前长方形的面积比是（9∶1）。（板书：放大后和放大前面积的比9∶1）

师：仔细观察3∶1和9∶1这两个比，你又有什么发现呢？

生1∶9是3的平方倍，1是1的平方倍。

师：你找到了数据之间的联系，数感真强！那谁再来用文字总结一下？

生2：如果把一个长方形按a∶1的比放大，放大后与放大前面积的比是a2∶1。

师：你能结合字母式把你的发现说出来，真厉害！

（二）大胆猜想，细心验证

师：是不是所有长方形按比例放大后面积比一定等于对应边平方的比呢？感觉上是，能马上下结论吗？因此这只是我们的一个猜想！（板书：猜想）

师：接下来怎么办呢？

生：举例验证。

师：你不仅说出了自己的想法，还把解决问题的方法告诉了大家，真不错！

生：验证。（板书：验证）

师：怎么验证呢？

生1：按照2∶1的比放大……

师：我知道你的意思了，你打算按照2∶1的比放大，再算一算是不是？

生2：我们可以把这个长方形按不同的比放大，看一看是否符合这个规律。

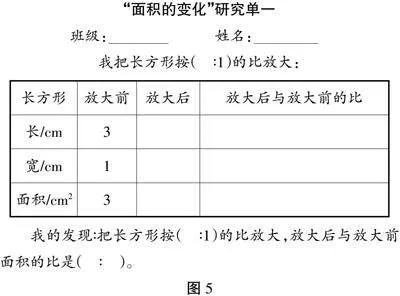
师：是啊，我们可以再举些例子进行验证。请大家完成研究单一（出示图5）。

“面积的变化”研究单一

班级： 姓名：

我把长方形按（ ∶1）的比放大：

师：谁来和我们一起分享你举的例子？

生1：把一个长方形按照几：1的比放大，放大后与放大前面积的比是几的平方比1。

师：数学讲究简洁美，谁能说得更简洁一些？

生2：把一个长方形按照x∶1的比放大，放大后与放大前面积的比是x2∶1。

师：刚才这位同学结合字母x把规律表示出来，非常简洁明了！如果用字母n，谁再来说一说。

生3：如果把一个长方形按n∶1的比放大，放大后与放大前面积的比是n2∶1。

师：你一下子就找到了关键，真是“火眼金睛”！

生总结：如果把一个长方形按n∶1的比放大，放大后与放大前面积的比是n2∶1。

师：同学们，我们刚才通过举例进行验证，这些例子举得完吗？如果有“漏网之鱼”，万一有不符合规律的呢？想一想我们还有没有其他的方法可以验证。

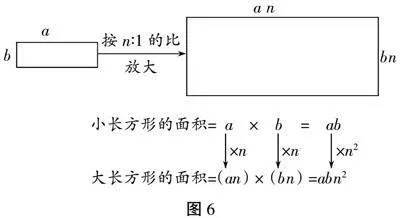
生说师出示PPT（见图6）。

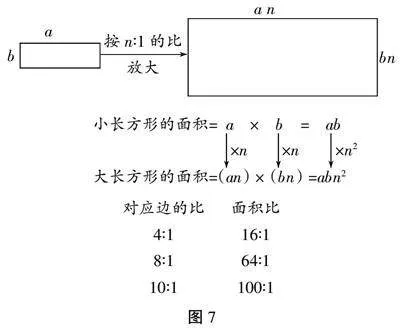
师：结合字母式，你发现大长方形和小长方形的面积有什么关系呢？

生：把小长方形的长扩大n倍，宽也扩大n倍，面积就扩大n2倍。

师：（出示图7）回顾我们刚才学习的内容，我们能举例验证，还能结合公式推理进行验证，通过验证我们就能总结规律（板书：总结），规律是什么？

生总结（师板书）：如果把一个长方形按n∶1的比放大，放大后与放大前面积的比是n2∶1。

师：大家总结得真不错！

（反思：结合算式、图形、公式推理等多种方法，发现长方形对应边和面积之间的联系。接着学生观察数据，发现面积比和长度比有着密切的联系，进而提出猜想，并举例进行验证。举例虽简易但不能穷尽，教师继续发问“是否有更严密的证明方法”，将学生的思维引向深入。有了前面多种证明方法的铺垫，学生自然而然地想到能结合公式推理。通过严密的公式论证，学生不仅能总结规律，还能培养推理论证能力，锻炼思维。）

三、探索其他平面图形面积比与长度比的关系

（一）由长方形想到其他平面图形

师：刚才我们研究的是长方形，接下来你打算研究什么？

生1：我打算研究圆。

生2：我打算研究平行四边形、圆、梯形、三角形。

师：你一下子说了这么多，真是个爱探索的孩子。

生3：我打算研究正方形。

师：正方形是一个特殊的长方形，长方形的规律正方形也适用吗？你可以探究一下哦。

生4：我打算研究不规则图形。

师：你的想法真独特！

（二）小组合作，验证猜想

师：接下来，四人小组合作进行研究，在合作之前请听活动要求。

活动要求：

1.每组任选一个图形，研究按比例放大后面积比与对应边的比之间的关系。

2.选择举例或结合公式推理验证你们小组的猜想。

3.组内交流你的想法，记录在研究单二上。

师：都讨论好了吗？哪一组上来汇报一下你们的研究成果？

预设1：

生1：选择一个三角形用数据验证。

师：你的例子举得真好！请回座位，还有同样选择了三角形，但方法不同的同学吗？

生2：结合公式推理。

师：解释得很有条理！请回座位。

师：还有研究其他图形的吗？

预设2：

生1：我选择圆，举例验证。

生2：我也选择圆，结合公式推理验证。

师：你们不仅会举例，还能结合公式推理进行验证，又联系了比的基本性质的相关知识，很好。

刚才这3组同学分别研究了平行四边形、三角形、圆，其他同学的研究和他们的发现一样吗？那现在，我们最终能得到什么结论呢？

师生共同总结并板书：把一个图形按照n∶1的比放大，放大后与放大前面积的比是n2∶1。

（三）前后呼应，应用知识

师：回顾一下我们课前的小故事，这两个人到底谁占便宜了呀？为什么？

学生回答后教师评价。然后说：巴依老爷最近正在修缮庄园，让我们一起去看一看。（播放录音）走进庄园，草地上有一个自动洒水装置。我打算把洒水装置的射程由3米扩大到6米，洒水面积将扩大几倍呢？

学生回答后教师播放录音：接着，请到我的房间来看一看。最初我给这间屋子铺正方形地砖，正好需要100块边长40厘米的地砖。可是最近我打算把地砖的边长调整为80厘米，现在需要多少块呢？

学生回答后，教师总结：没错，边长由40cm调整为80cm就扩大了2倍，因此面积就会扩大4倍，所以块数就要用……

师：是啊！应用刚才的研究成果，我们还能解决实际问题呢！（板书：应用）

（反思：通过多组汇报，师生共同总结规律。学生掌握规律后，教师带领学生回到课前小故事，利用今天学的知识，学生能高效地解决问题。接着教师让学生继续帮助巴伊老爷解决问题，有趣的故事吸引了学生的目光，一个又一个问题被学生一一破解，学生在欢笑中体会学习数学的价值！）

四、大胆猜测，迁移类推

师：根据这个结论，大胆猜一猜，还能提出哪些猜想呢？（同桌互相交流）

生1：把一个图形按照1∶n的比缩小，缩小后与缩小前面积的比是1∶n2。

师：是啊，把比的前后项换个位置，又能说出一个不一样的猜想。

生2：把一个图形按照m∶n的比（放大/缩小）变化，变化后与变化前面积的比是m2∶n2。

师：你真厉害，提出了一个更普遍的猜想。

生3：把一个图形按照n∶1的比放大，放大后与放大前体积的比是n3∶1。

师：你是根据面积这个词想到了体积，真会联想。

生4：把一个图形按照1∶n的比缩小，缩小后与缩小前体积的比是1∶n3。

师：你能结合前面两位同学的发言进一步提出猜想，真会学习！

生5：把一个图形按照m∶n的比变化，变化后与变化前体积的比是m3∶n3。

师：这些都只是我们的猜想，接下来怎么办？只有通过验证我们才能总结规律。

（反思：教师让学生大胆猜测，引导学生从面积想到周长，从平面图形想到立体图形。从二维教学联想到一维和三维。教师从整体出发，让学生的学习更加完整，感悟智慧的生长。）

五、总结提升

师：通过今天的学习，你有什么收获呢？

生1：如果把一个图形按照n∶1的比放大，放大后与放大前面积的比是n2∶1。

生2：我们要认真观察、比较数据，才能发现规律。

生3：我们在探索规律的时候会经历“猜想—验证—总结—应用”这四个过程。

师总结：数学世界充满了未知，希望同学们在今后的学习中，能多思多想，大胆猜测，细心验证，得出结论，并应用到我们的日常生活中。

（反思：教师通过教学活动，让学生充分体验“猜想—验证—总结—应用”这四个环节。学生不仅掌握了探索规律的一般方法，还学会了用数学知识解决实际问题。学生的科学素养得以形成，创新意识得以迸发，智慧得到了生长。）

编辑：曾彦慧

作者简介：李莹洁（1996—），女，本科，二级教师，研究方向：数学教学。