新课标背景下培养学生发散性思维的思考与实践

【摘要】实施促进学生发展的教学活动，教师可通过一题多解、解题方法提炼、多思巧问、总结基本图形等策略培养学生的发散性思维。激发学生学习兴趣，引发学生积极思考。培养学生良好的学习习惯，形成积极的情感态度和价值观，从而促进学生综合素养的有效提升。

【关键词】初中数学;一题多解；基本图形;发散性思维

新课程目标的确定，立足学生核心素养发展，集中体现数学育人价值。在基础教育阶段，应该帮助学生形成适应个人发展和社会发展需要的品格和解决问题的素养与关键能力，立德树人。

一、发散性思维培养的必要性

发散性思维是创新意识的基础。发散性思维（Divergent Thinking），又称辐射思维、放射思维、扩散思维或求异思维，是从不同角度、不同层面、不同维度正反两方面分析问题。因而视野开阔，思维活跃，会产生大量新颖的解题思路。可以通过“一题多解”“一事多写”“一物多用”等方式培养学生发散性思维能力。几何题往往会出现开放性、非常规、一题多解等特征，这些特征都跟发散性思维有密切联系，所以对几何题的一题多解更容易培养学生的发散性思维。注意从小培养发散性思维，才能为创新人才培养打下良好的基础。

二、发散性思维培养的有效性

核心素养落实的阵地在于课堂，实践在于师生。在初中数学教学中几何以平面几何为主。其中图形的运动是难点，图形的运动包括平移、翻折、旋转，特别是翻折、旋转运动是难中之难。笔者以一题多解的方式帮助学生突破难点，顺便复习整个初中几何体系。一题多解是培养学生发散性思维的有效途径，同时培养了学生的创新意识，也为创造性思维的培养铺路。本文将从翻折、旋转的一题多解为例来谈谈初中数学教学中如何培养学生的发散性思维，最后培养出具有创新意识的人才。

三、一题十解发散性思维探究

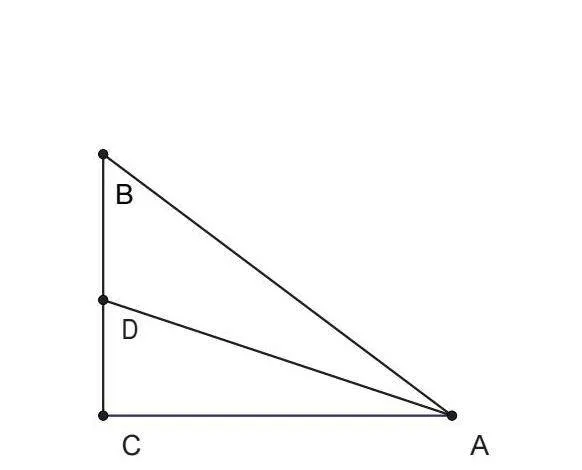
题目：如图，已知在中，，BC=3，AC=4，点D是线段BC上的一点，把沿直线AD翻折，使AC正好与AB重合，求线段BD的长。

解析：本题运用了初中大部分几何知识。这些知识虽出现在不同年级、不同章节，但是是相互联系的，又是螺旋式上升的。各种方法的出现符合学生年龄特征和认知规律。对素养的培养也是逐渐递增的，从抽象能力、运算能力、几何直观、空间观念，到推理能力、模型观念，甚至创新意识。

1.六七年级方法，构造图形结构，总结基本图形。目标是通过实践掌握“图形的性质”。

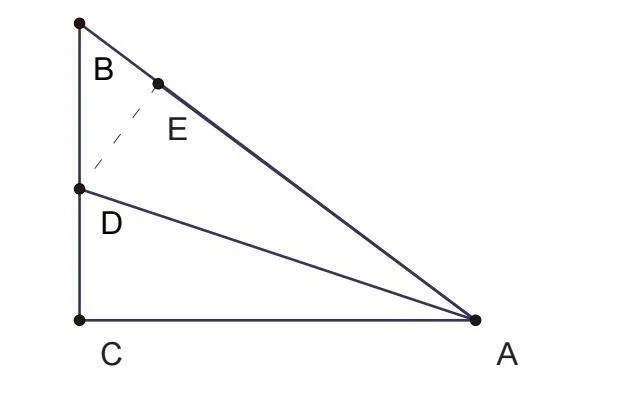
方法（1）面积法：过D作DE⊥AB，垂足为E，先证明≌或者由角平分线定理可得CD=DE。

再由S△ABC=S△ACD+S△ABD

×3×4＝×4×CD+×5×DE

得CD=，则BD=

解析：在七年级第一学期第十一章图形的运动中，我们刚学习了图形的翻折和旋转运动。很多有效方法还没学习，本方法利用六年级三角形面积和七年级全等三角形解答。

2.八年级方法，构造图形结构，结合方程函数坐标系。目标感悟数形结合掌握“图形与坐标”。

方法（2）勾股定理法：设CD=DE=x，由全等可知AE=CA=4，BE=1，BD=3-x，由勾股定理BD2=DE2+BE2（3-x）2=x2+12，x=，则DE=3-x=

解析：在八年级第一学期第十九章几何证明中学习了勾股定理。本方法利用这个定理解出了这一题，间接证明了勾股定理可以用面积法证明，因为上一种方法是面积法解出的。

方法（3）数形结合函数法：如图，建立直角坐标系，并延长AD交y轴于F，由角平分线和AC平行

于y轴得，所以BF=AB=5，A（3，4），F（0，-5）易得直线AF：y=3x-5当y=0，则BD=

解析：在八年级第二学期第二十章一次函数的学习后，学生可以利用一次函数的性质，根据数形结合的特点解出本题，也为以后的解析几何的学习埋下种子。

3.九年级方法，常见基本图形，适用范围更广。目标提升抽象能力掌握“图形的变化”。

方法（4）8字型法：过B作BF∥AC交AD的延长线F，由角平分线和平行易得，

所以BF=AB=5，由三角形一边的平行线性质定理得，

解析：在九年级第一学期第二十四章相似三角形平行线性质定理学习后，利用定理的比例式解决本题，并顺便抽象出“8字形”。“8字形”是初中的常用的基本图形，必须记住并熟练运用。

方法（5）A字型法：过D作DG∥AC交AB于G，由角平分线和平行易得∠GDA=∠GAD，所以DG=AG

由三角形一边的平行线性质定理得，

，，，，

解析：“A字形”也是通过三角形一边的平行线性质定理总结出的基本图形。同样“A字形”也是初中必须掌握的基本图形。对基本图形的熟练才能更快更准确地解出题目。

方法（6）相似三角形法：设CD=DE=x，由△BDE∽△BAC得得，BD=3-x=

解析：在九年级第一学期第二十四章中学习了相似三角形，相似法是对三角形一边的平行线定理的进一步归纳提炼并总结。适用的范围更广，能解决的题型更多。

方法（7）三角比法：由，得，CD=DE=，则BD=BC-CD=

解析：在九年级第一学期第二十五章锐角的三角比中，可以利用三角比的性质使格式更简单。

4.拓展内容法，抽象几何图形，解题快速方便。目标提高学生应用意识。

方法（8）角平分线成比例法：由角平分线分线段成比例定理三角形内角平分线分对边所得的两条线段和这个角的两边对应成比例。（可以由面积法证明）

解析：本方法利用拓展知识，角平分线成比例法，是对面积法的深刻理解，当然也可以用上面的“8字形”互相证明。说明很多定理之间相互联系，并且相互印证的。

方法（9）割线定理法：以线段AD为直径画圆，因为∠ACD是直角，所以点C在圆上，记圆与AB的交点为E，AD是直径，AD平分∠BAC，易得AE=AC=4，BE=1由割线定理：从圆外一点引圆的两条割线，这一点到每条割线与圆交点的两条线段的积相等。

BD·BC=BE·BA，3BD=1×5，BD=

解析：在九年级第二学期拓展二第二章直线和圆中的割线定理。本方法巧妙的利用了割线定理解决，同时说明了圆的知识在几何证明中也非常有用，并且也比较简单。

5.高中解题法，从模型观念到数据观念。目标为初中高中知识的过渡。

方法（10）半角倍角法：通过上面的方法可知

∠BAC的正切是，它的半角∠DAC的正切是。同时也可以得到∠ABC的正切是，它的半角∠CBE的正切是这样可知正切是和的两个角的和是45°。记住这些结论以后填空选择题碰到可以秒解。

，得，

，

解析：在高中一年级第二学期第五章三角比中

半角倍角公式如。利用这些

公式可以快速转化半角和倍角的三角比。

四、发散性思维促进创新意识

在数学教学中，若将经典例题充分挖掘一题多解。注重对例题等认真教学，不但可以在初三复习阶段抓好基础知识点，还可以激发学生的求知欲望。一题多解是让学生跳出单一思维模式，多种角度、多方位审视分析题目，而不是局限于某个知识点、某个章节，甚至某个体系，从而深刻理解某些题型。一题多解是培养学生发散性思维的常用而有效的方法，遵循学生的认识规律，遵循了发散性思维培养的规律，螺旋上升，逐段递进。一题多解也是课堂教学的一次重要反馈，在学习几种解法后，用另外几种解法检验是否学会。在实际教学过程中，让学生自己动手操作，用不同章节的知识点多方向、多纬度的分析问题，充分发挥自己的想象力、判断力、思考力。经常让学生多思考更多方法，一题多解，这样发散性思维也会慢慢培养出来。发散性思维是创造意识的前提，只有不断提升发散性思维，才能培养出具有创新意识的人才。

【参考文献】

[1]中华人民共和国教育部.义务教育数学课程标准（2022年版）[S].北京：北京师范大学出版社，2022.