基于核心素养的初中数学解题教学设计与研究

摘 要：解题教学是数学教学的重要组成部分。文章在“双新”“双减”背景下，从数学解题教学存在的困惑出发，对核心素养要求下的解题教学进行了研究，提出数学解题教学应该教什么题，以“六步四化”进行解题教学设计，旨在优化课堂效果，提升教学质量，培养学生的核心素养。

关键词：核心素养；数学解题教学；结构化

中图分类号：G633.6 文献标识码：A 文章编号：1673-8918（2024）32-0069-04

作者简介：蓝咏梅（1987～），女，畲族，浙江丽水人，浙江省杭州市惠兴中学，研究方向：解题教学。

一、 问题的提出

根据中共中央办公厅、国务院办公厅印发《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》，文件中指出“要优化教学方式，提升课堂教学质量”。《义务教育数学课程标准（2022年版）》（以下简称“新课标”）首次明确提出义务教育阶段数学课程要培养的学生核心素养，课程目标和课程内容的确定以核心素养为导向。

然而，如何探究优化路径提升教学质量成为当前迫切需要思考的问题，解题教学作为数学课堂教学的重要组成部分，存在较多困惑。

一是教师之困：教师自认为讲得很清楚，很到位了，但是学生再遇到同样类型的题目还是不会做。若是教师给予学生足够的思考时间，上课时间有限导致教学任务无法完成。教师没有相应教学模式可借鉴，缺少学习资源。

二是学生之困：学生自认为上课听懂了，能解决问题了，但是自己再遇到同样类型的题目还是不会做。学生花了大量的时间反复练习，自认为已经掌握了这些题，但是题目条件或题目情景改变之后就不会了。学生没有积累相应的数学活动经验，也没有反复应用这些经验的机会。

二、 理论基础

新课标指出，课程内容组织重点是对内容进行结构化整合，探索发展学生核心素养的路径。同时指出为实现核心素养导向的教学目标，不仅要整体把握教学内容之间的关联，注重教学内容的结构化，还要把握教学内容主线与相应核心素养发展之间的关联。

三、 数学解题教学应该教什么题

要想在有限的时间内实现解题教学效率最大化，教师首先要选“好题”。章建跃博士在《数学教育随想录》中提出，“好题”应与重要的数学概念和性质相关，能够体现基础知识的联系性，解题方法自然、多样，具有自我生长的能力；从培养思维能力的角度，则指问题是自然的，对学生的智力有适度的挑战性，题意明确、不纠缠于细枝末节，表述形式简洁、流畅、好懂。综合考虑后，笔者选择了一道条件简洁、图形简单、解法多样的母题。

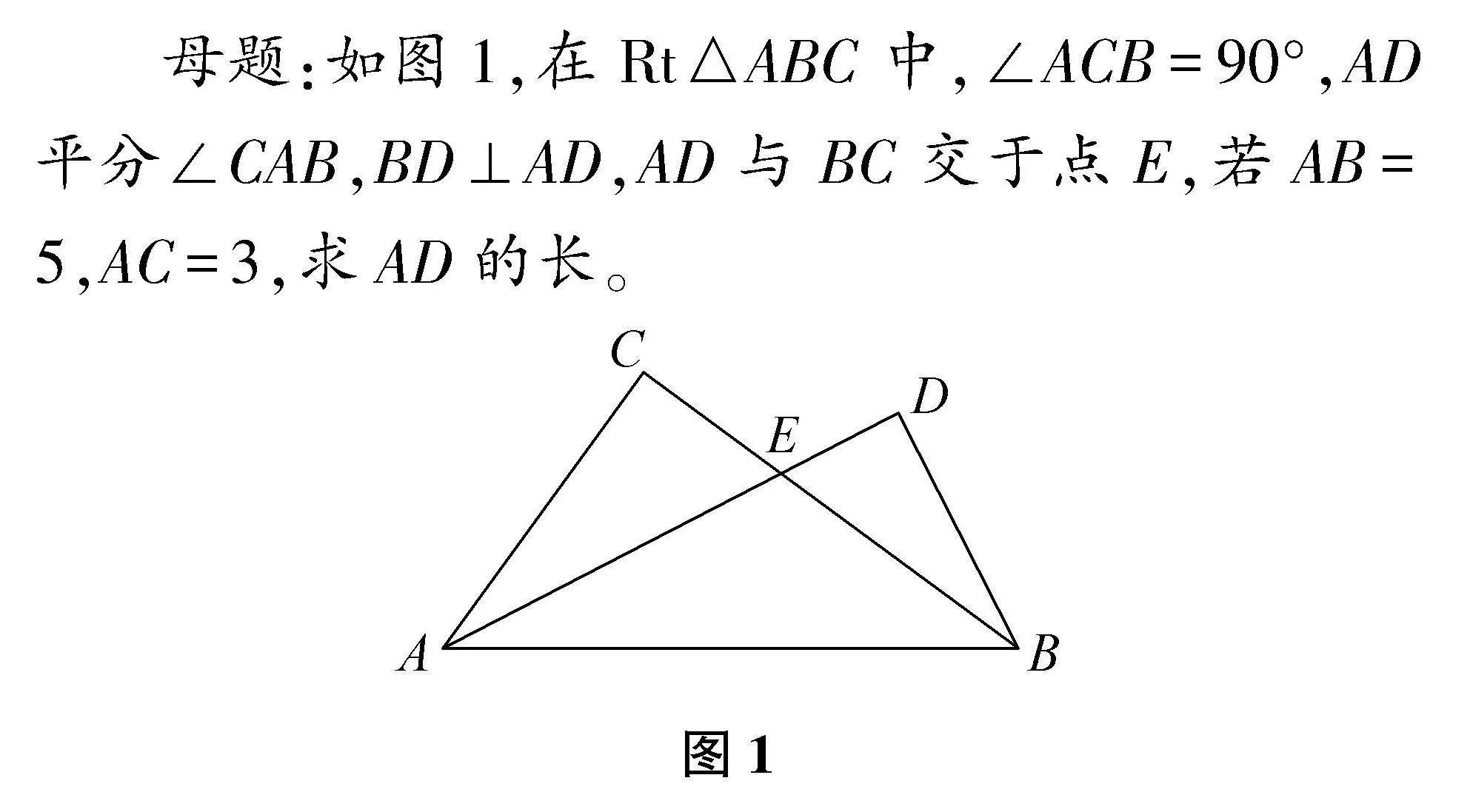
母题：如图1，在Rt△ABC中，∠ACB=90°，AD平分∠CAB，BD⊥AD，AD与BC交于点E，若AB=5，AC=3，求AD的长。

图1

为了让学生从不同的角度选择不同的方法解决问题，笔者将原题中的圆隐去，激发学生多维思考。

四、 数学解题教学的设计路径

通过反复地实践，笔者总结了初中数学解题教学设计的六步路径。即根据条件写出显性条件和隐形条件“教审题”；根据分析法和综合法寻找解题思路“教联想”；根据不同思路和视角寻找解题方法“教一题多解”；分析知识的本质，更换知识情境、图形，学生反复得到经验“教多解归一”；根据已有知识和条件进行变式拓展，使知识结构化“教拓展”；通过系列活动使学生积累基本活动经验，从而达到方法结构化，能力结构化，经验结构化“教反思”。

通过解题教学设计的六步路径，获得“四化成果”（图2），即引导学生在实践中梳理知识形成知识线，实现知识结构化；多视角和思路寻找“方法集”，实现方法结构化；研究过程中培养不同能力，形成“能力群”，实现能力结构化；运用经验解决不同问题，获得“经验域”，实现经验结构化。以期在“双新”背景下优化课堂教学，提升教学质量，真正提升学生的核心素养。

图2 解题教学四化成果

（一）教审题

问题是数学的心脏，学生正是在解决一个个数学问题的过程中加深对数学概念的理解，达到巩固数学知识，锻炼和发展思维能力的目的。那么，要解决问题第一个过程便是审题。对审题方法和技巧的研究有利于学生正确找到问题和条件的关系，快速联想到问题解决所需的知识点。

已知条件可分为直接的已知条件（显性条件）和间接的已知条件（隐性条件），隐性条件不直接应用于解答过程，往往容易被忽视，从而使学生思维受阻。

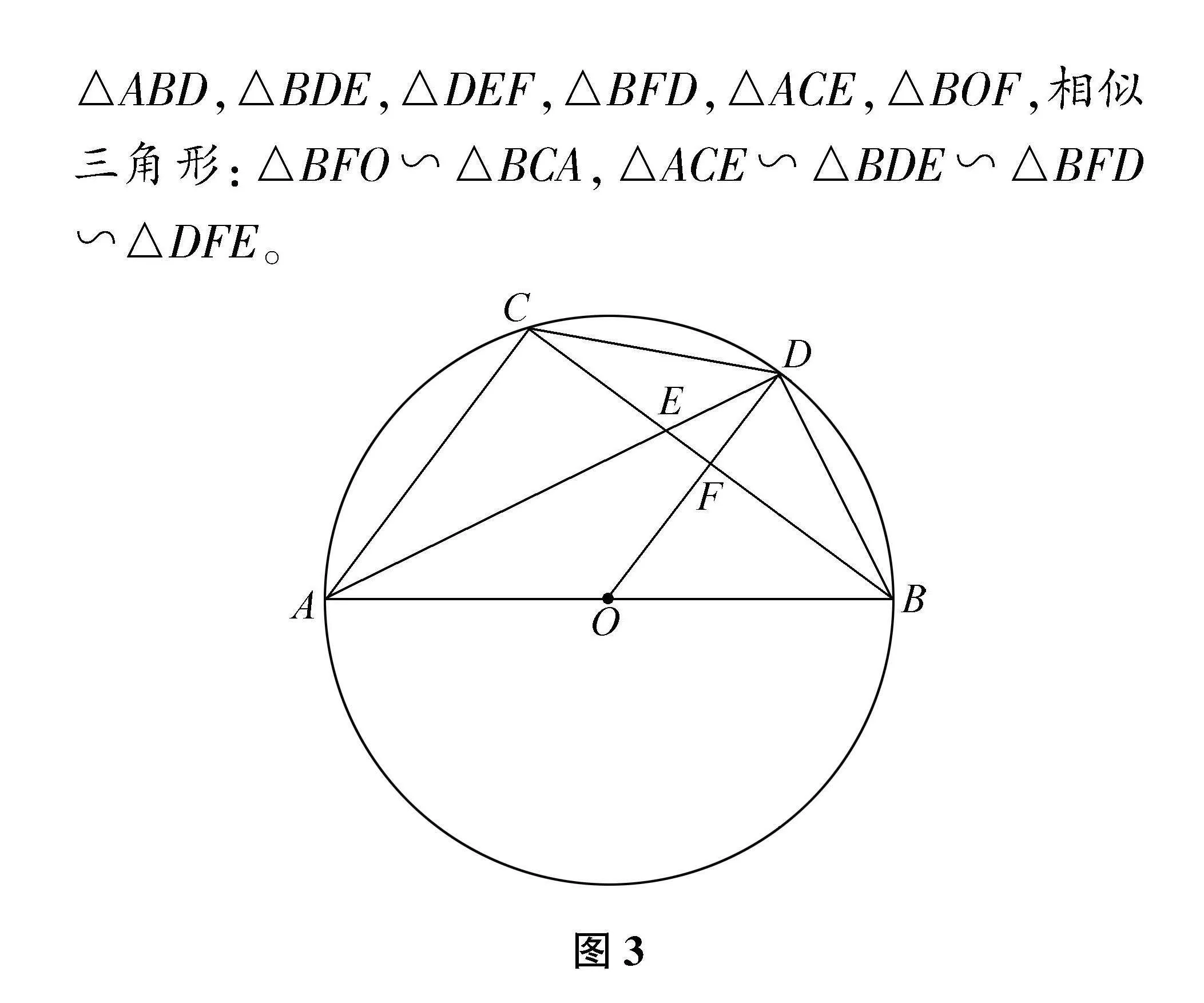
如母题中含有的显性条件：∠ACB=90°，AD平分∠CAB，BD⊥AD，AB=5，AC=3，隐性条件（图3）：①有关角的结论：∠CAD=∠BAD=∠CBD=∠ADO，∠BAC=∠BOD，∠ACB=∠ADB=90°；②有关弧、线段的结论（A，B，C，D四点共圆）：CD=DB，CD=DB，OD∥AC，OD垂直平分BC，……；③等腰三角形：△AOD，△BOD，△BCD，直角三角形：△ABC，△ABD，△BDE，△DEF，△BFD，△ACE，△BOF，相似三角形：△BFO∽△BCA，△ACE∽△BDE∽△BFD∽△DFE。

图3

（二）教联想

在平时教学中，教师希望学生看到题目的已知信息（特别是图形的特征），然后联想到有关性质定理，得到解题思路，从而解决问题，由于时间紧张，教师对学生的思维特点不了解等原因，容易出现学生“看到”而“联想不到”的情况，如何解决这样“尴尬”的现象呢？

一般的解题思路主要体现三类思维特征：一是以已知信息为基础，结合图形联想有关几何图形的性质和定理，从而得到新的信息，即由因导果——综合法；二是以待求的结果为起点，通过变形，转化，猜想等，寻找使待求结论成立的条件，即由果索因——分析法；三是从解决问题的整个角度来看，在综合法和分析法单向思维的基础上，进行综合分析，找到会合点，回顾已知信息，对已有的思路进行评估和调整，做出合理的猜想。

教师要引导学生善于前思后想，通过条件梳理，利用启发式问题帮助学生联想，找到解题的突破口，同时回顾求线段长的基本方法，结合联想的结果和求线段长的基本方法找到解决方案。分析法和综合法是解决问题的通法，对较难的问题，需要这两种方法的“会合”，基于以上分析，笔者认为可以用以下的分析方式。通过条件可以联想到角平分线性质定理，角平分线加垂直构造等腰三角形，角平分线分线段成比例定理，四点共圆。也可以通过求线段长的方式出发，等积法，勾股定理，相似，三角函数等。

（三）教“一题多解”

“一题多解”有助于联结不同领域知识间的关联，综合知识碎片，让问题由点成线、由线及面，形成完整的知识体系，帮助学生多层次、广视角、全方位地认清数学问题，达到方法结构化。

［视角一］在图1基础上，根据AD平分∠CAB联想到了角平分线的性质定理，从而有方法一、方法二和方法三（图4）。

方法一：角平分线性质定理+等积法

通过角平分线性质定理知CE=EF，在直角三角形BEF中，由勾股定理求出EF和AE，通过△ABE的面积求出BD和AD。

方法二：角平分线性质定理+相似

同方法一求得CE=32，BE=52，再利用△BDE∽△ACE，计算得到DE的长，从而求出AD的长。

图4

方法三：角平分线性质定理+三角函数

同方法一求得CE=32，BE=52，再利用 sin∠CAE=CEAE=sin∠DBE=DEBE，计算得到DE的长，从而引出求出AD的长。

［视角二］根据AD平分∠CAB，BD⊥AD联想得到△ABG是等腰三角形，从而有方法四、方法五。

方法四：角平分线+垂直+勾股定理

通过AD是角平分线和AD⊥BD得到△ABG是等腰三角形，从而得到AG，CG的长，进而得到BG，AD的长。

方法五：角平分线+垂直+相似

从方法四中我们已经得到△ABG是等腰三角形，点D是BG的中点，过点D作DH∥BC交AG于点H，通过△BDE∽△ACE得到BD的长，从而知道AD的长。

［视角三］根据AD平分∠CAB联想到角平分线分线段成比例定理，从而有方法六。

方法六：角平分线分线段成比例定理+相似

通过角平分线分线段成比例定理求出CE，BE的长，再根据△BDE∽△ACE，求出BD，AD的长。当然这里可以利用cos∠CAE=cos∠BAD进行计算。

［视角四］根据∠ACB=90°，BD⊥AD联想到点A，B，C，D四点共圆（图5），利用垂径定理，托勒密定理以及圆的轴对称性，从而有方法七、方法八、方法九和方法十。

方法七：垂径定理+中位线定理

通过垂径定理知道OD垂直平分BC，由中位线定理知OF，DF的长，通过勾股定理便可求BD，AD的长。

方法八：托勒密定理+勾股定理

由托勒密定理得：AC×BD+AB×CD=AD×BC。

图5

方法九：圆的对称性+勾股定理

过点D作DH⊥AB交AB于点H，交⊙O于点K，根据垂径定理得BD=BK=CD，所以DK=BC=4，DH=2，在Rt△ODH中，OD=52，DH=2，所以OH=32，AD=25。

方法十：旋转变换

将△ACD绕点D逆时针旋转得到△MDB，则△ADM是等腰三角形，从而得到AD的长。

（四）教“多解归一”

“多解归一”是让学生将各种方法进行归纳整理，找到知识的根源，从而建立知识系统，总结解决问题的基本方法，最终达到“做一题，会一类，通一片”的目的，进一步提升数学核心素养。这是落实解题教学主导作用的主要环节。

如图6，AB是半圆的直径，BC是半圆的弦，BC沿弦BC折叠交直径AB于点D。

图6

（1）当AD=BD=5时，则BC的长为 ；

（2）当AD=4，BD=6时，则BC的长为 。

通过上述的练习，学生能将已经得到的数学活动经验应用于这样的问题解决过程中，通过这样的学习模式，学会审题，学会联想，学会“一题多解”，学会反思，从而培养数学核心素养。

（五）教拓展

在解题教学中，我们不仅要教会学生解这道题、这类题，同时要引导学生在这个基本图形的条件下，还能不能提出新的问题，进行进一步拓展。本节课中笔者设计了以下问题串。

追问1：你能用直尺和圆规画出这个图形吗？学生不能解决这个问题往往是不能将条件中的显性和隐性条件进行综合分析，这时若是能利用尺规作图将图形画出来，说明学生能分析出问题解决的思路。

追问2：你能求出直角三角形ABC的外接圆半径，内切圆半径吗？

追问3：你能求出等腰三角形ABG的外接圆半径，内切圆半径？

追问4：你能求出扇形OBD的面积、BD的长吗？若要方便计算，需要怎样改变条件？

追问5：你能梳理有关轴对称的知识网络结构图吗？通过这个问题，引导学生将零散的知识进行梳理，用知识网络结构图进行展示。

（六）教反思

教师要引导学生反思、提炼，形成数学学习和研究的基本经验。若不经过反思，学生得到的经验是零散的，获得的解题技能是短暂的。完成解题后，它需要一个梳理、内化的过程。让学生回顾如何审题，如何分析显性和隐性条件，遇到障碍之后如何突破，数学基本活动经验的获得需要经历“活动——反思——活动”的过程。

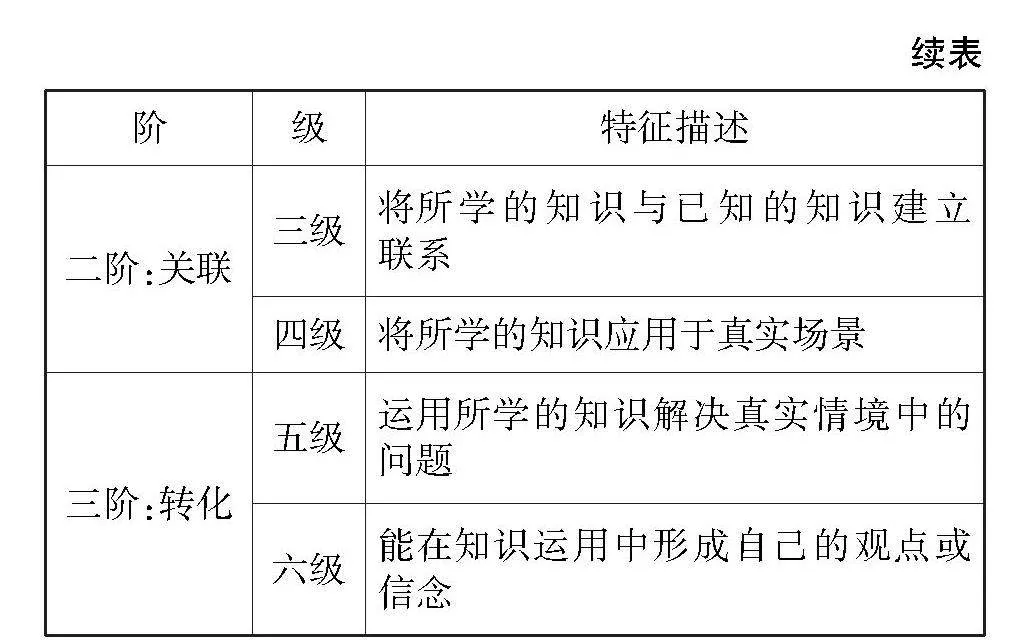
因此，解题教学应当着重开发学后反思的支架功能，通过设计包括“复述”“关联”和“转化”的进阶的反思路径，构建学后反思的“三阶六级水平”（表1），帮助学生认识自己的水平、管理自己的学习、反思自己的能力，使得我们的学生不仅能够在新旧知识间、知识与生活间建立“联结”，而且能够通过反思建立起知识与自我间的“联结”。

从课堂效果看，隐去之前的⊙O，学生的解题思路更开阔了，同时对比十种方法，学生体会到利用圆的知识解决这个问题的优势，体会“道是无圆却有圆，圆中自有新天地”，同时利用角平分线的性质定理和圆的知识都是源于轴对称性，进一步提升了知识高度。

五、 结论

匈牙利数学家波利亚在《怎样解题》中说：“解题过程就是一个运用探索法诱发学生灵感的过程，是形成和发展学生核心素养的基本途径。”笔者深感精确。通过近六年“六步四化”解题教学实践，笔者带领学生获得了一些基础知识和基本技能，在解决问题的活动中感悟到数学知识的发生发展过程，获得了数学基本活动经验，形成了带有数学学科特征的价值观，思维品质和关键能力，从而培养了学生的核心素养。

笔者将坚持以“六步四化”解题教学实践为研究起点，努力探索优化课堂，提升教学质量，在理解数学的基础上，不断研究题目、研究课堂、研究数学的本质，从而改进自己的教学方式，提升学生的思维品质，落实包括数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析等方面的数学素养。

参考文献：

［1］中华人民共和国教育部.义务教育数学课程标准［S］.北京：北京师范大学出版社，2022.

［2］章建跃.学习机会与核心素养的发展［J］.中小学数学（高中版），2023（5）：64-65.

［3］郭洪瑞，张紫红，崔允漷.试论核心素养导向的综合学习［J］.全球教育展望，2022，51（5）：36-48.

［4］邢成云，费祯红.“双减”背景下对数学解题教学的思考［J］.中小学课堂教学研究，2022（6）：11-14.