考虑顾客选择行为的BOPS自提门店个性化推荐

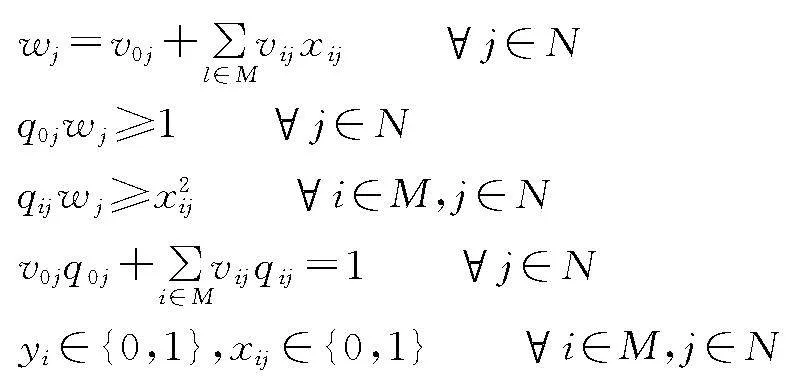
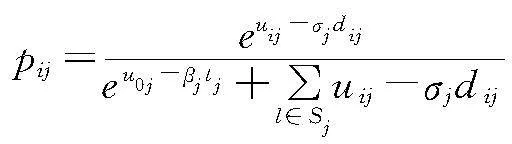
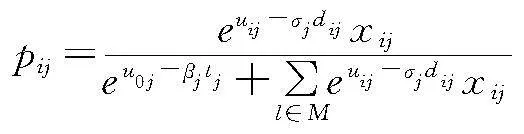
摘 要： 针对全渠道零售中的BOPS（在线购买门店提货）模式，给出了考虑顾客选择行为的自提门店推荐方法。此方法构建了结合商圈、距离以及预计送达时长的不同收货方式下顾客的效用函数，通过MNL选择模型来刻画顾客的选择行为，建立考虑顾客选择行为的以零售商利润最大化为目标的混合整数规划模型。其次，将模型转换成易于求解器求解的混合整数二阶锥规划模型。数值实验表明本文提出的自提门店的推荐方法可提升零售商的利润。最后，探讨了预计送达时长、顾客的距离敏感度与收益的关系。数值实验结果表明，零售商的总利润与预计送达时长呈正相关关系，零售商的总利润与顾客对距离的敏感度呈负相关关系。

关键词： 全渠道零售；BOPS；Multinomial Logit模型；二阶锥规划

中图分类号： F 252

文献标志码： A

Personalized Recommendation of BOPS Self-Pickup StoreConsidering Customer Choice behavior

Abstract： In the context of omnichannel retail， a method for recommending self-pickup locations for customers in the BOPS （Buy Online， Pick Up in Store） model has been proposed. This method constructs utility functions for customers under different delivery options， taking into account factors such as the shopping district， distance， and estimated delivery time. Customer choice behavior is characterized using an MNL （Multinomial Logit） selection model， and a mixed-integer programming model is formulated with the objective of maximizing retailer profit while considering customer choice behavior. Furthermore， the model is transformed into a mixed-integer second-order cone programming model that is amenable to solver-based solutions. Numerical experiments demonstrate that the recommended self-pickup location method proposed in this article can enhance the retailer's profit. Finally， the relationship between estimated delivery time， customer distance sensitivity， and revenue are explored. Numerical experimental results reveal a positive correlation between the retailer’s total profit and estimated delivery time， as well as a negative correlation between the retailer’s total profit and customer sensitivity to distance.

Key words： omnichannel retailing; Multinomial Logit Model; BOPS; SOCP

0 引言

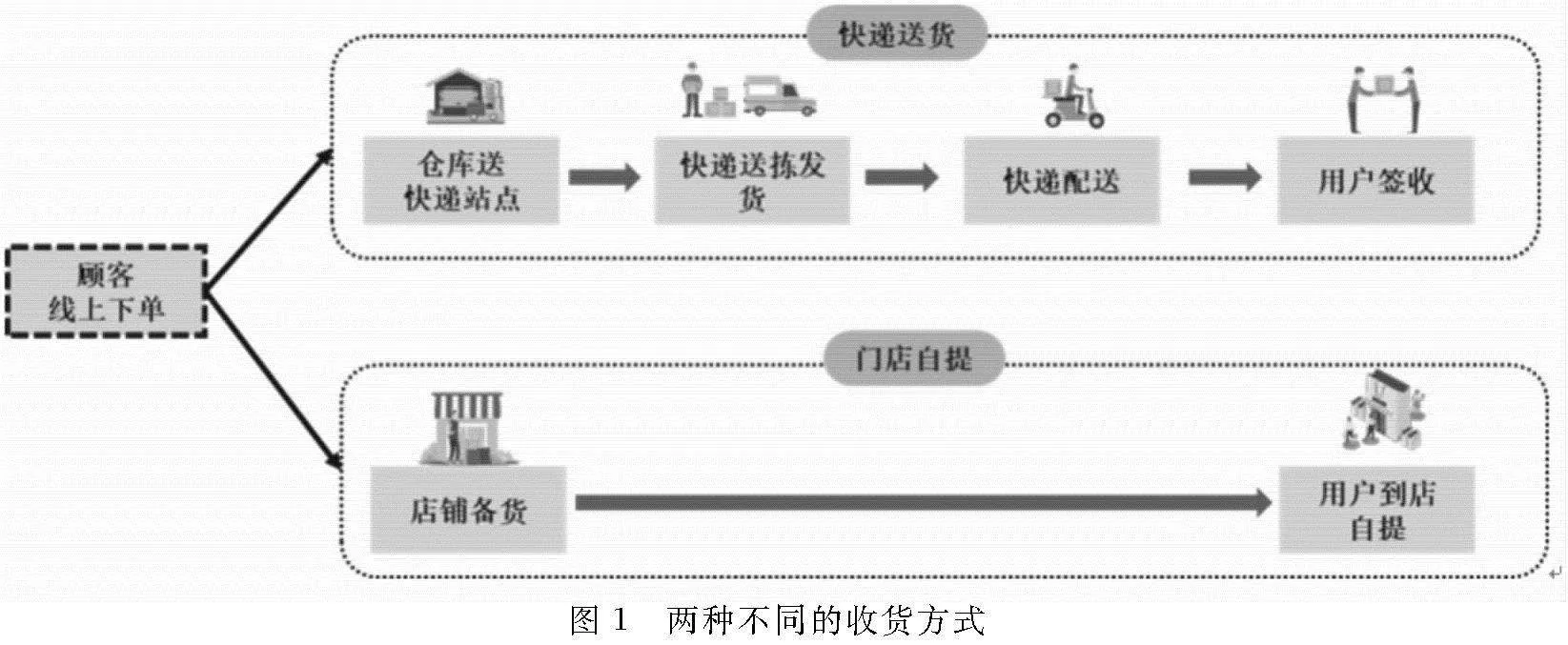
近年来，移动终端飞速崛起，依托移动平台的零售企业快速发展。根据 Statista 数据平台，预计 2024 年全球电子商务销售额将达到 6.388 万亿美元（Statista，2020）［1］。如此迅猛的增长，伴随着新技术的不断发展，大大提高了网上购物的普及率的同时也提高了消费者不断增长的期望值。零售业已经从以往的“以商品为中心”向“以顾客为中心”转变。为了满足消费者任何时候、任何地点、任何方式购买的需求，越来越多的零售商已经采用或正在过渡到全渠道零售［2-5］。在全渠道零售背景下，最流行的购物方式之一是BOPS（Buy Online and Pick Up in Store ）。BOPS渠道可以满足消费者对综合渠道的消费需求，提升消费者的消费体验。如图1所示，相比于快递送货，BOPS是打破最后一公里的模式，消费者完成了“商品到手”的最后一步，避免二次或多次配送。

对于商家而言，BOPS可以为线下门店带来流量，并有可能增加销售额［6］。UPS的一项研究表明，在使用BOPS渠道的人中，45%的人在店内提货时进行了新的购买［7］。因此，越来越多的零售商向他们的客户提供BOPS选项。零售系统研究（Retail Systems Research，RSR）报告显示，美国64%的零售商已经实施了BOPS［8］。对于顾客而言，BOPS 允许客户在线下订单并从他们家附近的商店提取已完成的订单，这为客户提供了线上和线下相结合的最佳体验。一方面，他们可以使用在线渠道进行研究、阅读评论、比较价格、付款，享受无忧购物的便利。另一方面，通过BOPS，顾客可以获得即时的满足，快速提取物品并且可以节省网购快递费，同时享受“无忧购物”的便利（他们的商品在到达时已经由商店工作人员挑选和包装）。

随着线上线下融合的全渠道零售兴起，BOPS模式成为供应链管理领域的热点问题。其中首要的问题是，确定为哪些门店开设BOPS服务以及如何为顾客推荐自提门店。首先开设到店自提服务，门店需要支出与实体店自提相关的运营费用，如为方便线上消费者的自提而增加的通道和设施。其次，顾客选择自提门店时，不仅会考虑距离的远近，而且还会考虑门店周围商圈的便利程度（例如，停车便利度、餐饮等服务）。

回顾已有研究，主要是关于全渠道零售的门店选址、定价、选品、订单履行的研究。虽然有部分关于BOPS模式下的研究，但没有BOPS模式下如何为顾客个性化推荐自提门店以及同时决策开设哪些门店为自提点的研究。目前，在为顾客推荐提货门店的研究中， 仍然是按门店距离顾客的远近进行推荐，并把所有的门店都设为自提点， 并没有考虑到门店及其周围商圈带给顾客的效用，以及开设过多门店为自提点会带来额外更多的成本。因而，综合考虑顾客的选择行为以及门店与顾客的距离对每个顾客推荐自提门店，同时考虑开设自提门店的成本是非常重要的。为此，本文给出了一个考虑顾客选择行为的自提门店推荐方法，该模型综合考虑了提供自提服务的成本、顾客对距离的敏感度、对预计送达时长的敏感度以及对店铺周围设施的效用。

1 文献综述

近年来，关于全渠道零售的研究引起国内外学者的广泛关注。Brynjolfsson等［9］ 和 Forman等［10］研究了如何确定多渠道的最优价格决策和均衡价格。高莹等［11］研究了参考质量效应下的体验类商品全渠道定价策略，强调了消费者体验感受对定价策略的影响。刘金荣和徐琪［12］分析固定销售价格和优化定价两种情形下Showrooms对定价、市场需求、利润和退货率的影响。Dzyabura 和 Jagabathula［13］以及Chen等［14］研究了线下渠道选品问题以最大化线上和线下渠道的利润。Faugère和Montreuil［15］研究了智能储物柜在全渠道物流中的使用，并强调了这些储物柜在提高最后一英里交付效率方面的潜力。Millstein 和 Campbell［16］ 建立了一个利润最大化优化模型，用于支持电子商务和商店发货的全渠道仓库的选址。最近，Arslan 等［17］考虑了一家计划将在线渠道整合到其运营中的实体零售商，并提出了一种用于在不确定性下设计全渠道分销网络的集成建模方法。胡祥培等［18］、Caro等［19］全面总结了过去关于全渠道零售的文献，并指出了未来的研究方向。值得指出的是，关于全渠道零售下的BOPS模式近年来也受到了学者的研究和关注。Du等［20］指出通过线下渠道或BOPS渠道购买的消费者可获得更多的产品信息及服务，其产品体验价值更高。Gallino 和 Moreno ［21］以及Gao和Su［22］分别从实证和理论的角度研究了网上购买、实体店提货的影响和启示。Jin 等［23］通过对ROPS和BOPS的比较，明确ROPS和BOPS两种履行模式的优点，得出了两种履行模式的最优采用策略。邱菊等［24］通过构建双渠道零售商和合作履行线上订单的第三方物流企业的博弈模型，研究零售商应何时采取BOPS 策略以及该策略对第三方物流服务定价和利润的影响。最后，本研究还涉及关于顾客选择行为的文献，顾客需要从推荐的自提门店进行决策，并且顾客的决策结果影响到零售商的总利润。本文使用多项式 Logit 模型（ MNL 模型） 描述消费者的选择行为。MNL模型的提出可以追溯至 Luce［25］，是学者们用来描述消费者选择行为的常用方法。

2 问题与模型描述

本研究所涉及的符号如下表1所示。

2.1 问题描述与假设

本文研究了一个全渠道零售下BOPS模式为顾客个性化推荐自提门店的问题。假设总共有m个实体门店，用集合M={1，2，…，m}表示；有n个顾客在线上进行下单，用集合N={1，2，…，n}表示。实体门店开设自提点功能会带来额外成本，假设每个实体门店开设自提通道所用的成本为ci，其中i∈M。顾客去线下门店取货，可以为线下门店带来额外的收益，包括顾客的二次消费以及客流量的增加所吸引更多的顾客到门店所带来的消费，这里用rij表示顾客j去门店i会带来的额外总收益。顾客j到门店i的距离为dij，不同顾客对距离的敏感度不同，用σj表示顾客j对距离的敏感度，σj越大表示顾客对距离的敏感度越高。假设网站页面显示快递邮寄给顾客的j的预计送达时长为tj，顾客对预计送达时长的敏感度为βj，βj越大表示顾客更偏向于更快拿到商品，即顾客对时间的敏感度越高。

基于以上假设，顾客j选择去店铺i自提商品所获得的效用可以表示如下：Uij=uij-σjdij+εij，其中第一项uij为顾客j去店铺i提货的正效用，即商品和店铺所在商圈给顾客带来的效用；第二项σjdij表示顾客去店铺i自提的负效用，即前往店铺带来的成本；εij为效用的随机项。同理，顾客选择线上邮寄的效用可以表示如下：U0j=u0j-βjtj+ε0j，其中第一项u0j为顾客j选择快递邮寄所购买的商品的正效用，第二项βjtj表示顾客等待快递的负效用，ε0j为效用的随机项。为了描述具有多个自提门店选择的顾客的选择行为，本文引入MNL （Multinomial logit model）模型，即假设{εij}，i∈{0}∪M是独立同分布的 Gumbel 随机变量。对于每个顾客j，给定推荐的自提门店的集合Sj，顾客选择去门店i∈Sj自提的概率为：

2.2 考虑顾客选择行为的BOPS自提门店推荐模型

目前，为顾客推荐提货门店的方法是按顾客距离店铺的远近进行推荐。具体如下，顾客首先在商家的APP小程序上选择要购买的商品；随后结账页面会弹出顾客是选择门店自提还是快递送货，如果顾客选择门店自提，APP页面会弹出为顾客推荐的一些取货门店。然而，顾客在选择门店时，往往不仅考虑到门店距离顾客的远近，还会考虑到门店附近的商圈以及便利程度。值得指出的是，以往的研究往往假设所有门店均开设了门店自提功能，现实中往往有些门店客流密度是可以不需要顾客到店自提来引流的，这样反而造成额外的成本浪费。因而，不同于传统距离导向的自提门店的推荐方法，本文综合考虑顾客的效用以及门店与顾客的距离为每个顾客推荐自提门店，同时考虑开设自提门店的成本进行个性化门店推荐决策。

我们构建以商家总收益最大为目标的混合整数规划模型，决策变量为：

那么顾客j选择去门店i自提的概率pij可以重新记作：

因此，我们得到以下非线性整数规划模型，记作模型（BOPS-IP）：

3 模型求解

该模型与模型（BOPS-IP）有相同的最优解，可以用目前一些优化求解器（如CPLEX和Gurobi）处理。

此外，根据文献［26］，我们可以通过添加McCormick有效不等式到模型（BOPS-CONIC）中，以加速模型（BOPS-CONIC）的求解速度。最终，我们得到可以直接用现有求解器进行求解的模型（BOPS-CONIC+MC），如下：

4 数值算例

本章节首先验证了本文所提出的推荐方法的有效性，然后分析了预计到达时间以及顾客对距离的敏感度对收益的影响。本文所有算例在 Windows 10 下利用Python语言编程并调用Gurobi实现。所有计算实验在 Intel Core i7-10710U CPU 1.61 GHz，16GB RAM 上运行，Gurobi 版本为10.0。

算例规模为n=50，m=20。参数的设置如下。顾客到门店的距离dij服从区间［1，5］的均匀分布，顾客对距离的敏感度σj服从区间［0，0.1］的均匀分布。由于我们这里考虑的是一个城市的顾客，因此假设预计送达时长对于所有顾客是一样的，这里预计送达时长tj=2。顾客对预计送达时长的敏感度βj服从区间［0，0.2］的均匀分布。顾客去店里自提的效用uij服从区间［0，2］的均匀分布，假设顾客选择快递邮寄的效用是相同的，即为u0j=3对于任意的j∈N。为顾客推荐的门店个数K=10。按照上述方式，我们生成十个不同的数据集。

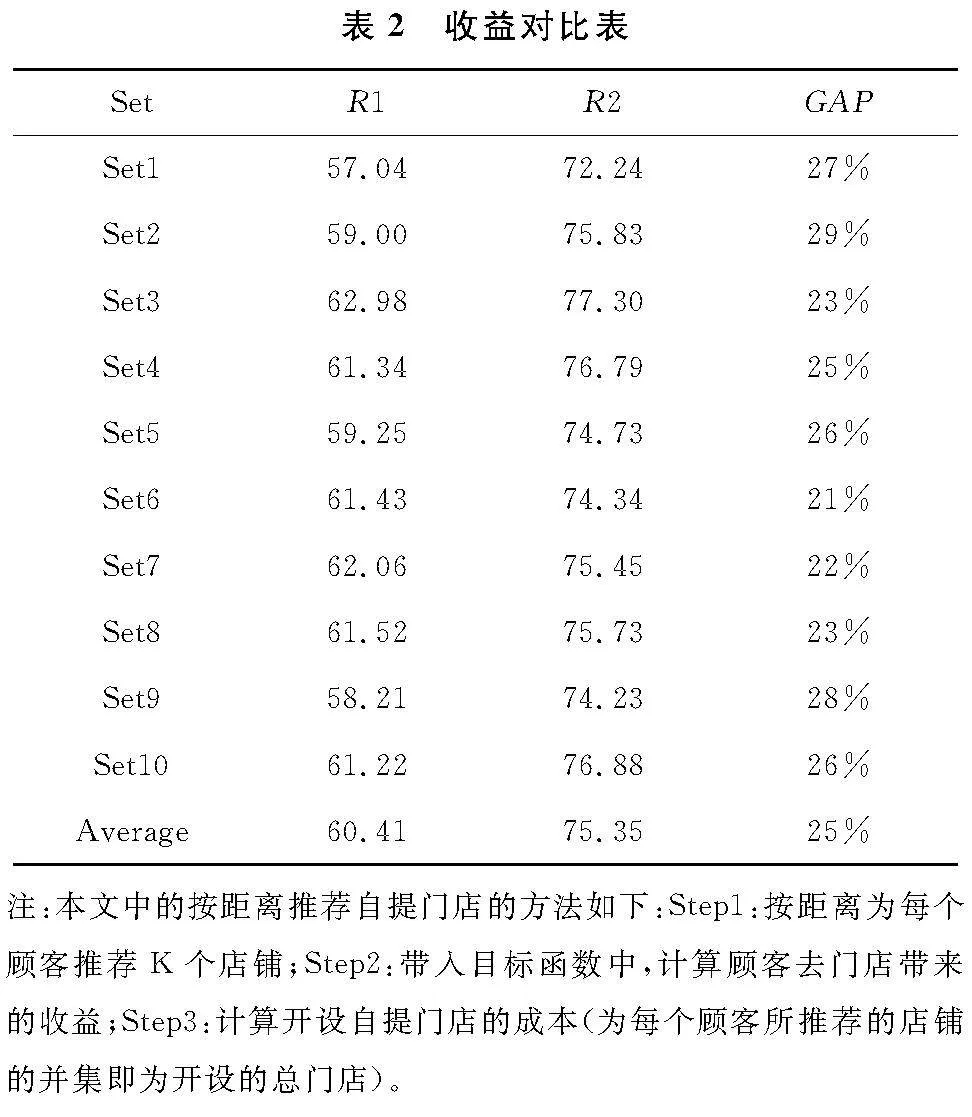
4.1 个性化为顾客推荐门店的有效性

4.2 预计到达时间对收益的影响

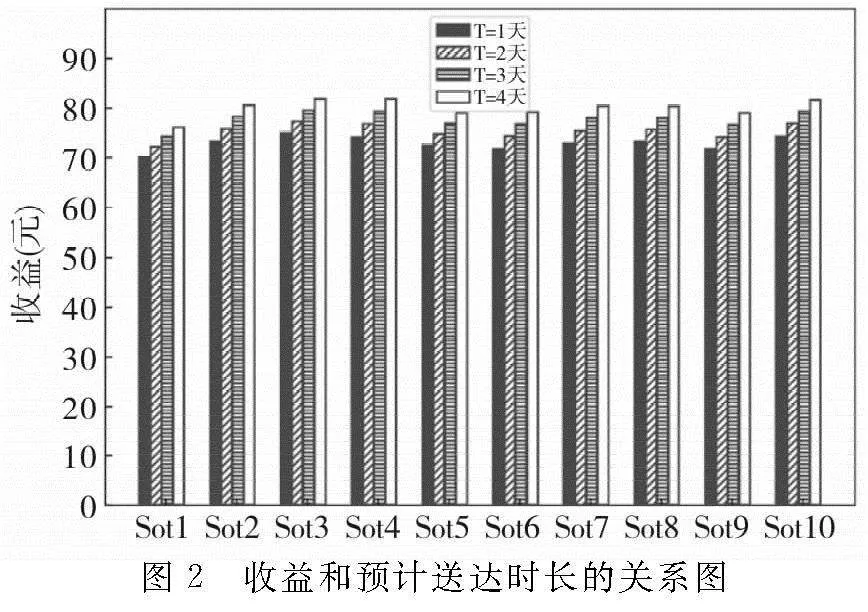
为了分析预计到达时间与收益的关系，本文分别计算预计到达时间为tj=1、tj=2、tj=3以及tj=4时上述10个算例对应的收益，计算结果如图2所示。在图2中，对于每个算例，从左到右每个柱子依次表示预计送达时长为1天、2天、3天以及4天时的收益。从图2中可以看出，每个算例中总的收益均随着预计送达时长的增加而增加。也就是说，当预计到达时间增加时，顾客选择线上邮寄的概率降低，选择去门店自提的概率增加，进而带来门店期望收益的增加。因此，商家可以为顾客设置更大的预计送达时长以引导顾客去线下门店提货从而增加门店客流量，进而增加线下店铺的收益。

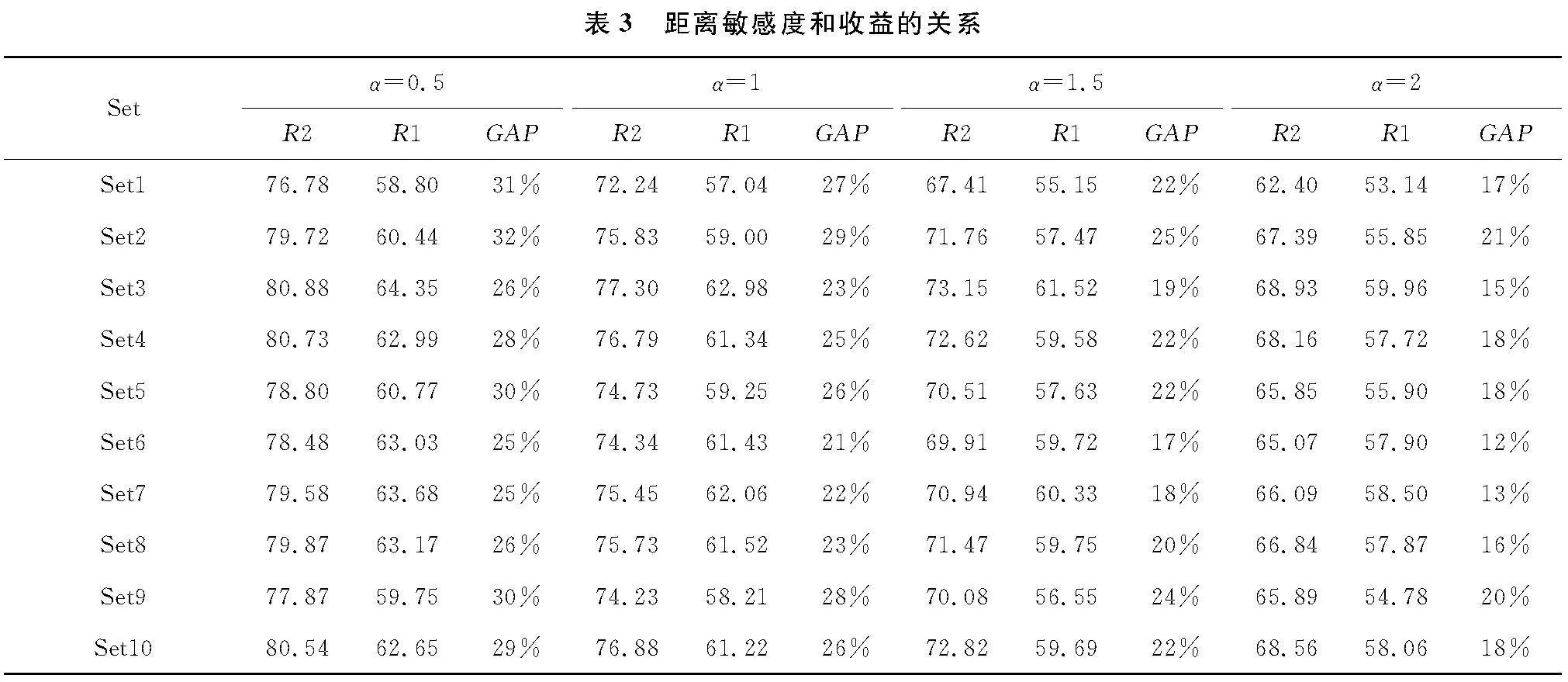
4.3 顾客的距离敏感度对收益的影响

5 小结

本文研究了全渠道零售下考虑顾客选择行为的BOPS自提门店推荐问题。针对此问题，本文将顾客对距离以及时间的敏感度刻画到顾客的效用中，通过MNL选择模型来刻画顾客的选择行为，构建了考虑顾客选择行为的以零售商利润最大为目标的混合整数规划模型，并将模型转换成易于求解器求解的混合整数二阶锥规划模型，通过添加McCormick有效不等式以提升求解速度。数值算例分析表明，相比于按距离为顾客推荐自提门店，本文提出的考虑顾客选择行为的BOPS自提门店推荐方法可以进一步提升零售商的利润。

文章进一步探讨了预计到达时间、顾客的距离敏感度与收益的关系。数值实验结果表明，零售商的总利润与预计到达时间呈正相关关系，商家可以为顾客设置更大的预计送达时长以促使顾客去线下门店提货从而增加门店客流量，进而增加线下店铺的收益；零售商的总利润与顾客对距离的敏感度呈负相关关系，当顾客对距离的敏感度比较高时，那么按距离给顾客推荐与本文所提出方法的收益的差异会逐渐缩小。此外，本文模型是在假设店铺内商品库存充足的前提下进行考虑的，对于库存有限时，如何考虑到不同店铺的库存为顾客推荐自提店铺是需要进一步分析的问题。

参考文献：

［1］ Statista. Retail e-commerce sales worldwide from 2014 to 2024［EB/OL］. https：//www.statista.com/statistics/379046/worldwide-retail-e-commerce-sales/.

［2］ BELL D R， GALLINO S， MORENO A. How to win in an omnichannel world［J］. MIT Sloan Management Review， 2014， 56（1）： 45-53.

［3］ BRYNJOLFSSON E， HU Y J， RAHMAN M S. Competing in the age of omnichannel retailing［M］. Cambridge： MIT， 2013.

［4］ CAI Y J， LO C K Y. Omni-channel management in the new retailing era： A systematic review and future research agenda［J］. International Journal of Production Economics， 2020， 229： 107729.

［5］ VERHOEF P C， KANNAN P K， INMAN J J. From multi-channel retailing to omni-channel retailing： introduction to the special issue on multi-channel retailing［J］. Journal of retailing， 2015， 91（2）： 174-181.

［6］ CLIFFORD S. Wal-Mart has a web plan to bolster in-store sales［EB/OL］. https：//www.nytimes.com/2011/03/11/business/11shop.html

［7］ UPS. UPS online shopping study： Empowered consumers changing the future of retail［R/OL］. Press release， June 3. United Parcel Service of America， Atlanta， 2015.

［8］ ROSENBLUM P， KILCOURSE B. Omni-channel 2013： The long road to adoption［R］. RSR 2013 Benchmark Report. Retail Systems Research， Miami， 2013.

［9］ BRYNJOLFSSON E， HU Y， RAHMAN M S. Battle of the retail channels： How product selection and geography drive cross-channel competition［J］. Management Science， 2009， 55（11）： 1755-1765.

［10］ FORMAN C， GHOSE A， GOLDFARB A. Competition between local and electronic markets： How the benefit of buying online depends on where you live［J］. Management science， 2009， 55（1）： 47-57.

［11］ 高莹， 胡祥培， 方艳， 等. 参考质量效应下的体验类商品全渠道定价策略研究［J］. 管理工程学报，2023，37（1）：147-157.

［12］ 刘金荣， 徐琪. 全渠道零售下 “Showrooms” 对需求分布， 定价和收益的影响研究［J］. 中国管理科学， 2019， 27（12）： 88-99.

［13］ DZYABURA D， JAGABATHULA S. Offline assortment optimization in the presence of an online channel［J］. Management Science， 2018， 64（6）： 2767-2786.

［14］ CHEN J， LIANG Y， SHEN H， et al. Offline-channel planning in smart omnichannel retailing［J］. Manufacturing & Service Operations Management， 2022， 24（5）： 2444-2462.

［15］ FAUGRE L， MONTREUIL B. Smart locker bank design optimization for urban omnichannel logistics： Assessing monolithic vs. modular configurations［J］. Computers & Industrial Engineering， 2020， 139： 105544.

［16］ MILLSTEIN M A， CAMPBELL J F. Total hockey optimizes omnichannel facility locations［J］. Interfaces， 2018， 48（4）： 340-356.

［17］ ARSLAN A N， KLIBI W， MONTREUIL B. Distribution network deployment for omnichannel retailing［J］. European Journal of Operational Research， 2021， 294（3）： 1042-1058.

［18］ 胡祥培， 王明征， 王子卓， 等. 线上线下融合的新零售模式运营管理研究现状与展望［J］. 系统工程理论与实践， 2020， 40（8）： 2023-2036.

［19］ CARO F， KK A G， MARTNEZ-DE-ALBNIZ V. The future of retail operations［J］. Manufacturing & Service Operations Management， 2020， 22（1）： 47-58.

［20］ DU S， WANG L， HU L. Omnichannel management with consumer disappointment aversion［J］. International Journal of Production Economics， 2019， 215： 84-101.

［21］ GALLINO S， MORENO A. Integration of online and offline channels in retail： The impact of sharing reliable inventory availability information［J］. Management Science， 2014， 60（6）： 1434-1451.

［22］ GAO F， SU X. Omnichannel retail operations with buy-online-and-pick-up-in-store［J］. Management Science， 2017， 63（8）： 2478-2492.

［23］ JIN M， LI G， CHENG T C E. Buy online and pick up in-store： Design of the service area［J］. European Journal of Operational Research， 2018， 268（2）： 613-623.

［24］ 邱菊，赵菊，房晓艺，等.基于第三方物流服务定价的零售商BOPS策略研究［J］.管理工程学报，2023，37（3）：169-177.

［25］ LUCE R D. Individual choice behavior： A theoretical analysis［M］. Courier Corporation， 2012.

［26］ SEN A， ATAMTRK A， KAMINSKY P. A conic integer optimization approach to the constrained assortment problem under the mixed multinomial logit model［J］. Operations Research， 2018， 66（4）： 994-1003.